基于最小二乘法的步态机器人运动轨迹辨识*

陈智勇， 张平改， 钱艳艳

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

自从机器人控制技术问世以来，其路径规划问题一直是一个热点[1]，许多研究人员在这个领域进行了大量的实验研究，并提出许多可行的方法.朱庆保[2]等选用了最近邻居策略、目标导引函数和概率搜寻策略，提出利用栅格法对蚂蚁觅食路径进行建模，从而获得一条最好运动轨迹；庄晓东[3]等参考了物体的运动和其位置的关系，提出了应用模糊概念建立动态的数学模型，从而构造出一种二维函数，最后通过模糊评价得出最佳运动轨迹；周郭许[4]等提出应用栅格法建立一种数学模型，并用求迷宫最短路程的算法，来求得机器人的最佳运动轨迹；唐国新[5]等在交叉算子的基础上，提出了一种改进的遗传算法，优化了在实际操作过程中遗传算子的进化效率，最终得到一条最佳的运动轨迹；周磊[6]等针对路径长度相同，但直线路径消耗的能量要小一点的问题，提出了引入模糊算法的方法，对蚁群算法进行改进，组成一种混合算法对运动轨迹进行研究；何娟[7]等结合了遗传算法与蚁群算法，提出了一种新型的遗传蚁群算法，先通过遗传算法得出初始运动轨迹分布，再采用蚁群算法求出其最优解，得到一条最佳运动轨迹；另外，冯治国[8]等先利用拉格朗日法建立系统的运动模型，并设计了比例-微分反馈控制法，同时引入径向神经网络来减小误差，实现无偏差轨迹控制，得到机器人最佳运动轨迹.

以上文献中,研究人员应用了大量的不同方法对机器人路径运动轨迹进行研究，取得了一定得成果.此处将在以上研究的基础上，先通过对人体步态特征参数进行测量并计算，再通过曲线拟合的方法，为其建立相对应的数学模型，从而得到步态机器人的运动轨迹.

1 步态机器人动力学特性

步行运动是一个周期性的运动过程，由于两条腿的运动是交替进行的，所以以其中一条腿来进行运动轨迹的研究.一个完整的步态运动是由支撑相和摆动相两个部分组成的，支撑相期包括第一个双足支撑相、单足支撑相和第二个双足支撑相，它约占整个步态周期的60%，其中双足支撑相约占20%，单足支撑相约占40%；而在摆动相期间，一条腿与地面接触，另一条腿处于摆动的状态，它约占整个步态周期的40%，步伐周期如图1所示.

图1 步伐周期图

在整个步态运动过程中，将下肢简化成如图2的模型，其中A,B,C 3点分别表示髋关节、膝关节、踝关节的转动中心，D点表示脚趾.利用摄像机测得A,B,C,D等4点在不同时刻的空间位置，并记录下其坐标值，为后期的角度计算提供数据.

下肢模型相邻两个点之间的连线长度lab，lbc，lcd的计算公式为

(5)

将式(1)到式(5)联立起来进行方程的求解，得到髋关节角度θhip、膝关节角度θknee、踝关节角度θankle的数学表达式分别为

将4个点的坐标值A(xa,ya,za)，B(xb,yb,zb)，C(xc,yc,zc)，D(xd,yd,zd)，代入θhip，θknee，θankle的表达式中，即可得到髋关节角度θhip，膝关节角度θknee和踝关节角度θankle的值.

图2 下肢简化模型图

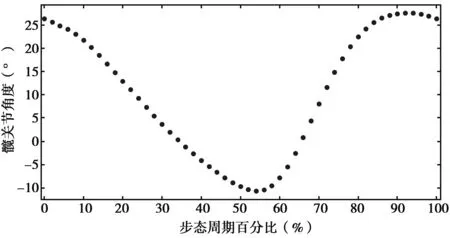
图3 髋关节的角度数据

2 步态机器人特征参数辨识

上述测得的步态特征参数是离散的，不能直接用来进行步态机器人运动轨迹的研究，还需通过数学方法来建立相对应的数学模型.此处应用最小二乘法来建立数学模型，并通过MATLAB拟合出来一条近似的曲线，能反映测量数据的变化趋势，可以最大程度排除随机误差的干扰，得到一个比较精确的数学模型.

2.1 髋关节角度特征模型

髋关节在一个周期内的角度数据变化规律如图3所示，从图中可以看出，髋关节在一个周期内先下降后上升，其中出现了一个波谷，所以可以选用正弦函数、余弦函数和常数组合在一起，通过3者的叠加构造一种傅里叶函数实现曲线的拟合.髋关节的角度数学模型通式为

θhip=a0+a1cos (xw)+b1sin (xw)+a2cos (2xw)+b2sin (2xw)+a3cos (3xw)+b3sin (3xw)

其中,θhip表示髋关节角度；x表示步态周期的百分比，取值范围为[0,100]；a0，a1，b1，a2，b2，a3，b3，w为髋关节拟合曲线方程系数.

按照髋关节的角度数学模型通式进行曲线拟合，在MATLAB中进行运算可以得到如图4所示的拟合曲线和如表1所示的拟合系数值.从图4中可以看出，用傅里叶函数拟合出来的曲线跟随角度的变化而变化，能符合角度的变化规律.

将表1拟合出来的系数代入髋关节角度数学模型通式中，可以得到其模型数学表达式为

为了验证髋关节拟合曲线的结果，现在利用最小二乘法对其残差进行计算，并通过MATLAB运行，可得到如图5所示的拟合曲线残差图和如表2所示的残差系数值.

图4 髋关节的拟合曲线

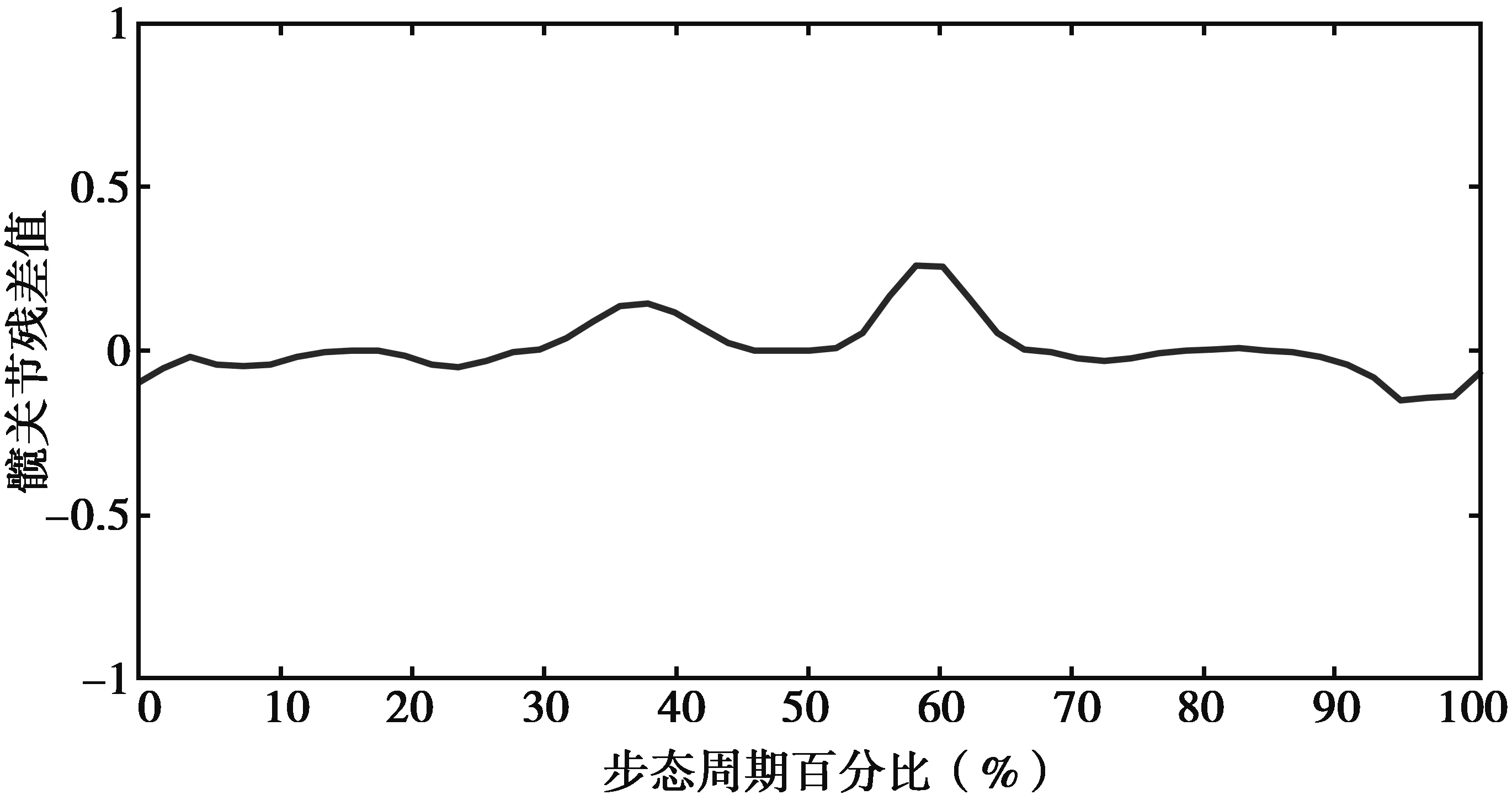
图5 髋关节拟合曲线的残差

表1髋关节的拟合系数值

系数项a0a1b1a2b2a3b3w系数值10.1318.51-3.119-2.135-2.335-0.322 81.2690.062 57

表2 髋关节残差系数值

从图5所示的髋关节拟合曲线的残差可以看出，拟合出来的曲线的残差在负0.15与0.3之间波动，残差比较小,能符合拟合的要求.从表2所示的髋关节残差系数值可以看出，残差的标准差为0.227 1，标准误差为0.999 7，符合标准差不超过1.5，标准误差不超过1的要求.

2.2 膝关节角度特征模型

膝关节在一个周期内的角度数据变化如图6所示，从图6中可以看出，膝关节在一个周期内上下起伏两次，其中出现了一个波谷、两个波峰，所以可以选用正弦函数、余弦函数和常数组合在一起，通过3者的叠加构造一种傅里叶函数实现曲线的拟合.膝关节的角度数学模型通式为

θknee=a0+a1cos (xw)+b1sin (xw)+a2cos (2xw)+b2sin (2xw)+a3cos (3xw)+b3sin (3xw)

其中,θknee表示膝关节角度；x表示步态周期的百分比，取值范围为[0,100]；a0，a1，b1，a2，b2，a3，b3，w为膝关节拟合曲线方程的系数.

按照膝关节的角度数学模型通式进行曲线拟合，在MATLAB中进行运算可以得到如图7所示的拟合曲线和如表3所示的拟合系数值.从图7中可以看出拟合出来的曲线跟随角度的变化而变化，能符合角度的变化规律.

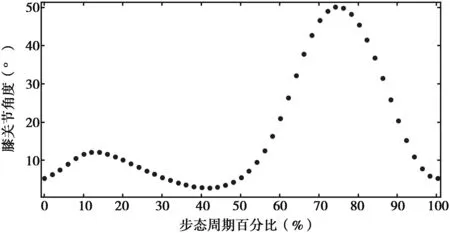
图6 膝关节的角度数据

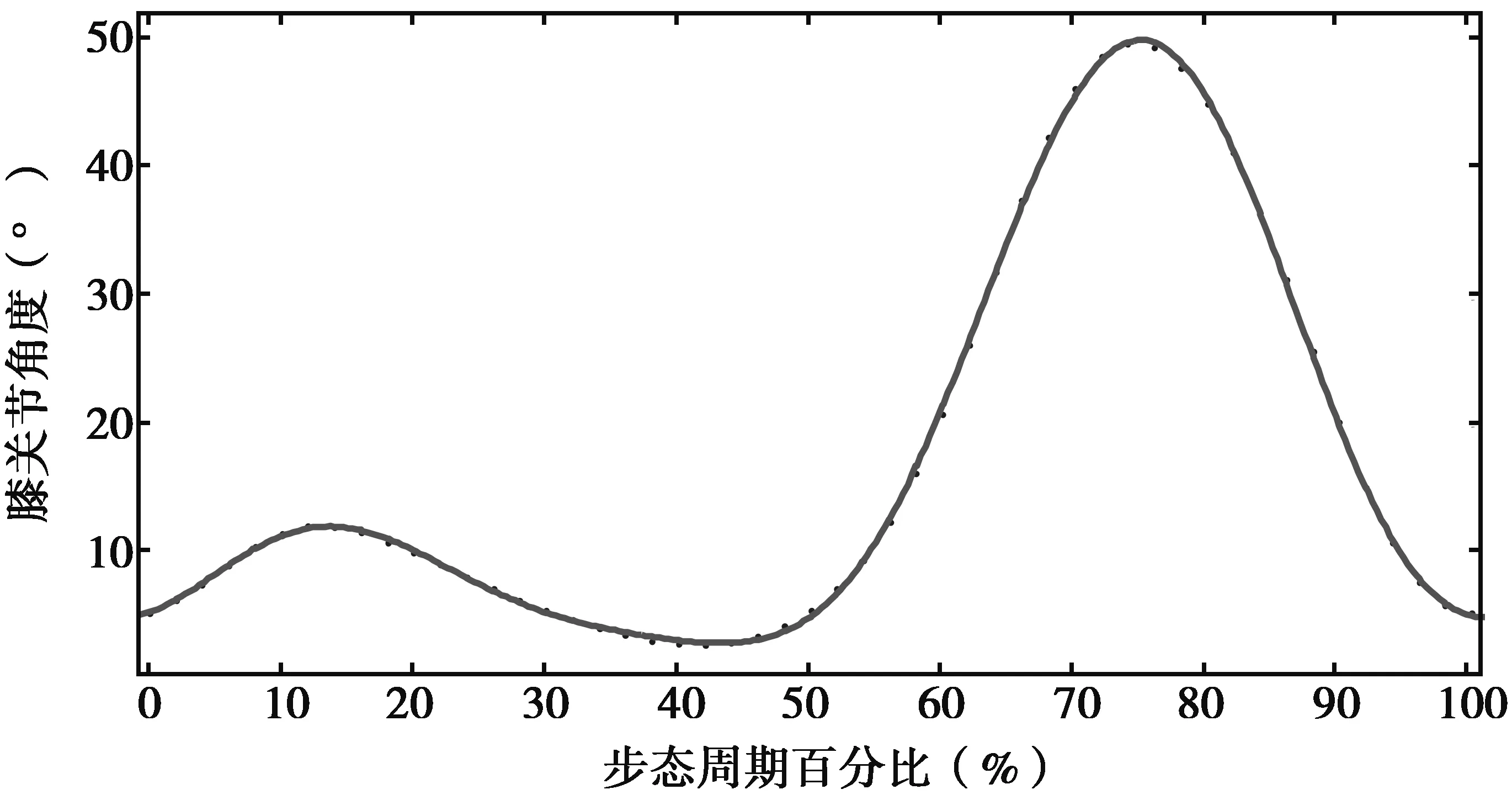
图7 膝关节的拟合曲线

表3膝关节的拟合系数值

系数项a0a1b1a2b2a3b3w系数值17.13-1.115-17.12-11.185.5870.622 83.9380.060 96

将表3拟合出来的系数值代入膝关节角度数学模型通式中，可以得到其模型数学表达式为

为了验证膝关节拟合曲线的结果，现在利用最小二乘法对其残差进行计算，并通过MATLAB运行，可得到如图8所示的拟合曲线残差图和如表4所示的残差系数值.

表4 膝关节残差系数值

从图8所示的膝关节拟合曲线的残差可以看出，拟合出来的曲线的残差在负0.25与0.25之间波动，残差比较小能符合拟合的要求.从表4所示的膝关节残差系数值可以看出，残差的标准差为0.324 5，标准误差为0.999 6，符合标准差不超过1.5，标准误差不超过1的要求.

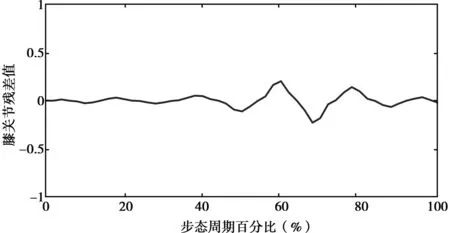
图8 膝关节拟合曲线的残差

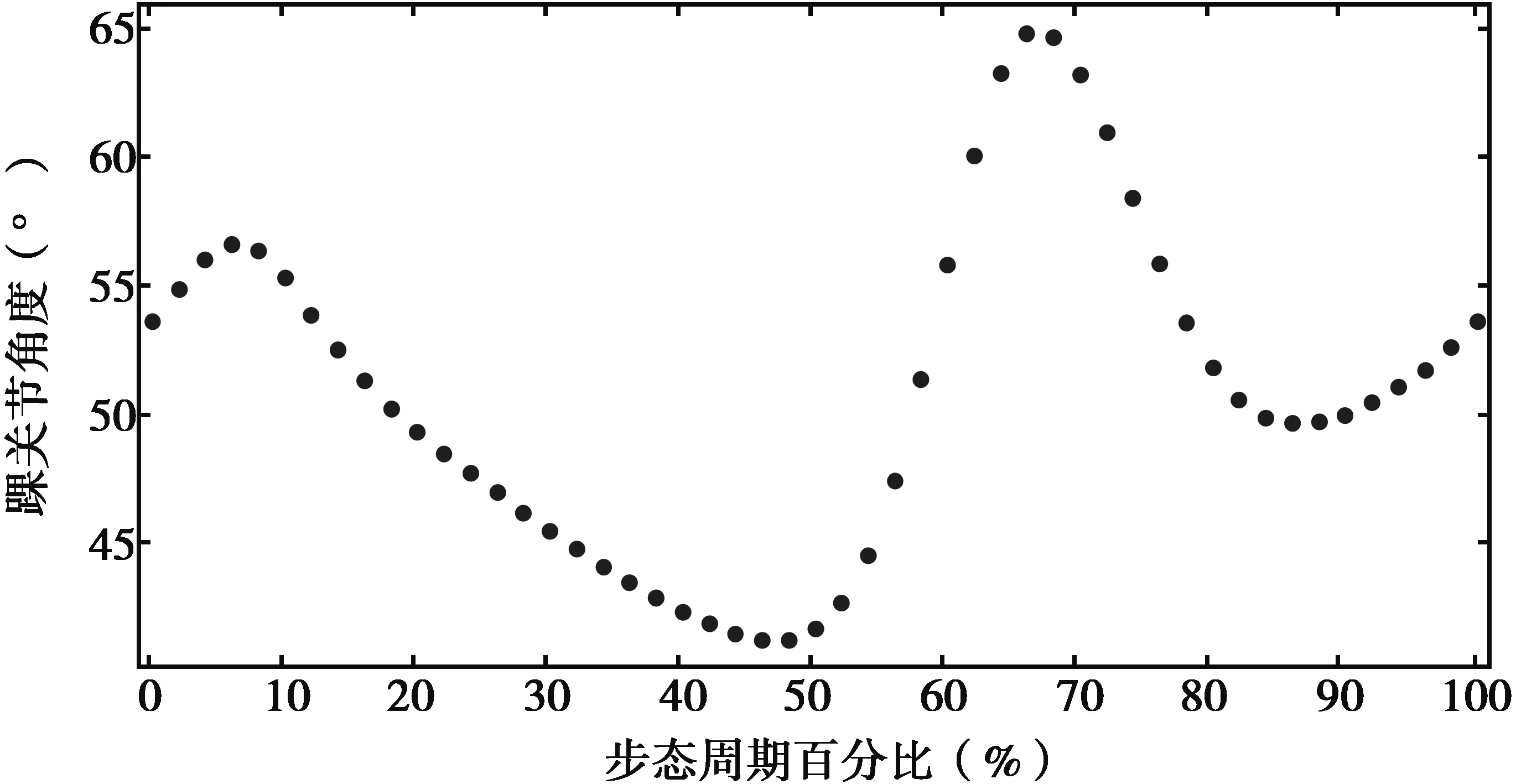
图9 踝关节的角度数据

2.3 踝关节角度特征模型

踝关节在一个周期内的变化趋势如图9所示，从图中可以看出，踝关节在一个周期内出现了两个波峰与两个波谷，它的变化趋势是先上升后下降，然后再上升后下降，最后上升，所以可以选用5个高斯函数组合在一起，通过叠加来实现曲线的拟合.踝关节的角度数学模型通式为

其中,θankle表示踝关节的角度；x表示步态周期的百分比，取值范围为[0,100]； a1，b1，c1，a2，b2，c2，a3，b3，c3，a4，b4，b4，a5，b5，c5为踝关节拟合曲线方程系数.

按照踝关节的模型通式进行曲线拟合，在MATLAB中进行运算可以得到如图10所示的拟合曲线和如表5所示的拟合系数值.从图10中可以看出拟合出来的曲线跟随角度的变化而变化，能符合角度的变化规律.

表5 踝关节的拟合系数值

将表5的拟合出来的踝关节系数值代入模型通式，可以得到踝关节角度模型的数学表达式

为了验证踝关节拟合曲线的结果，现在利用最小二乘法对其残差进行计算，并通过MATLAB运行，可得到如图11所示的拟合曲线残差图和如表6所示的残差系数值.

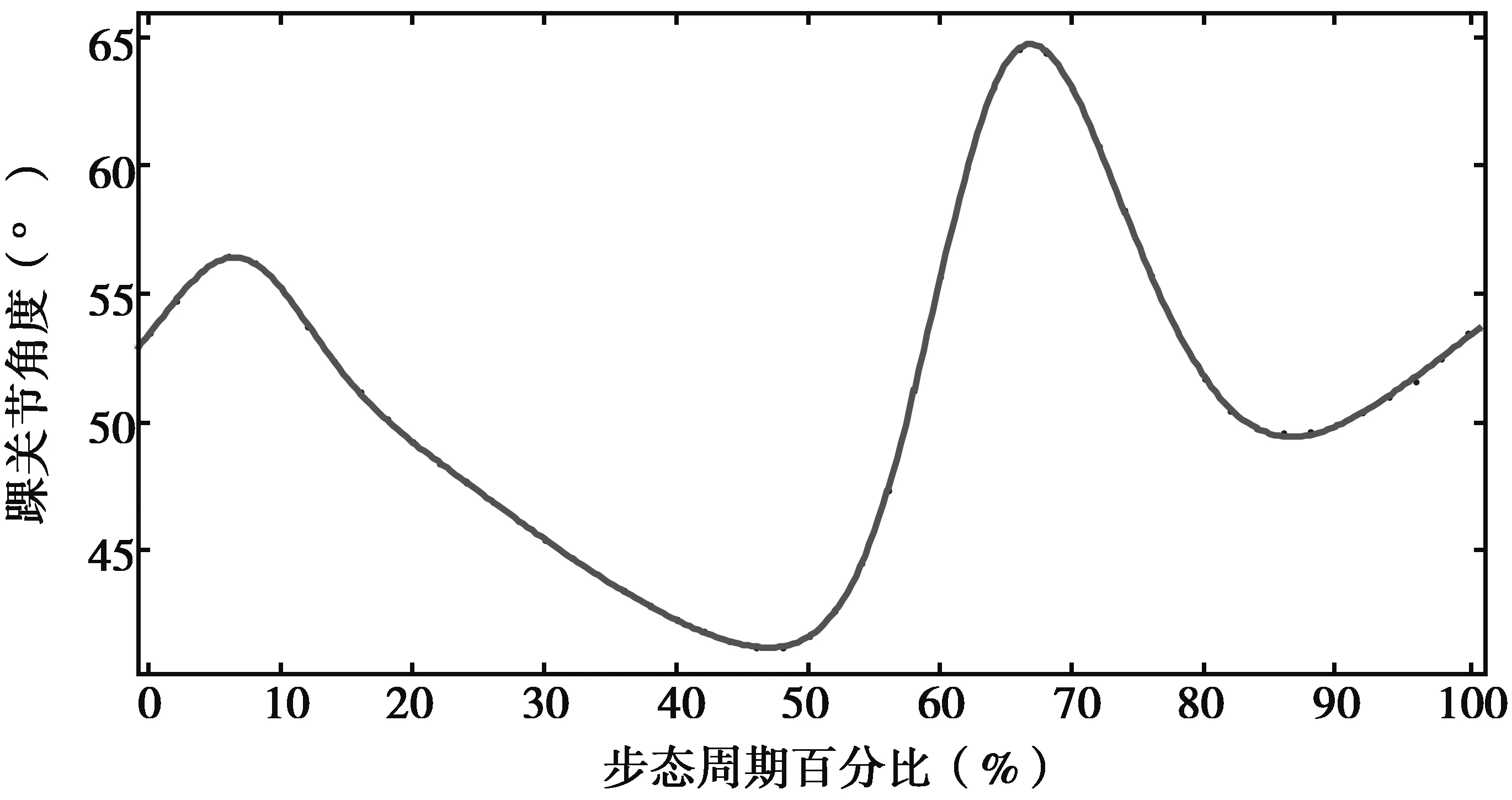
图10 踝关节的拟合曲线

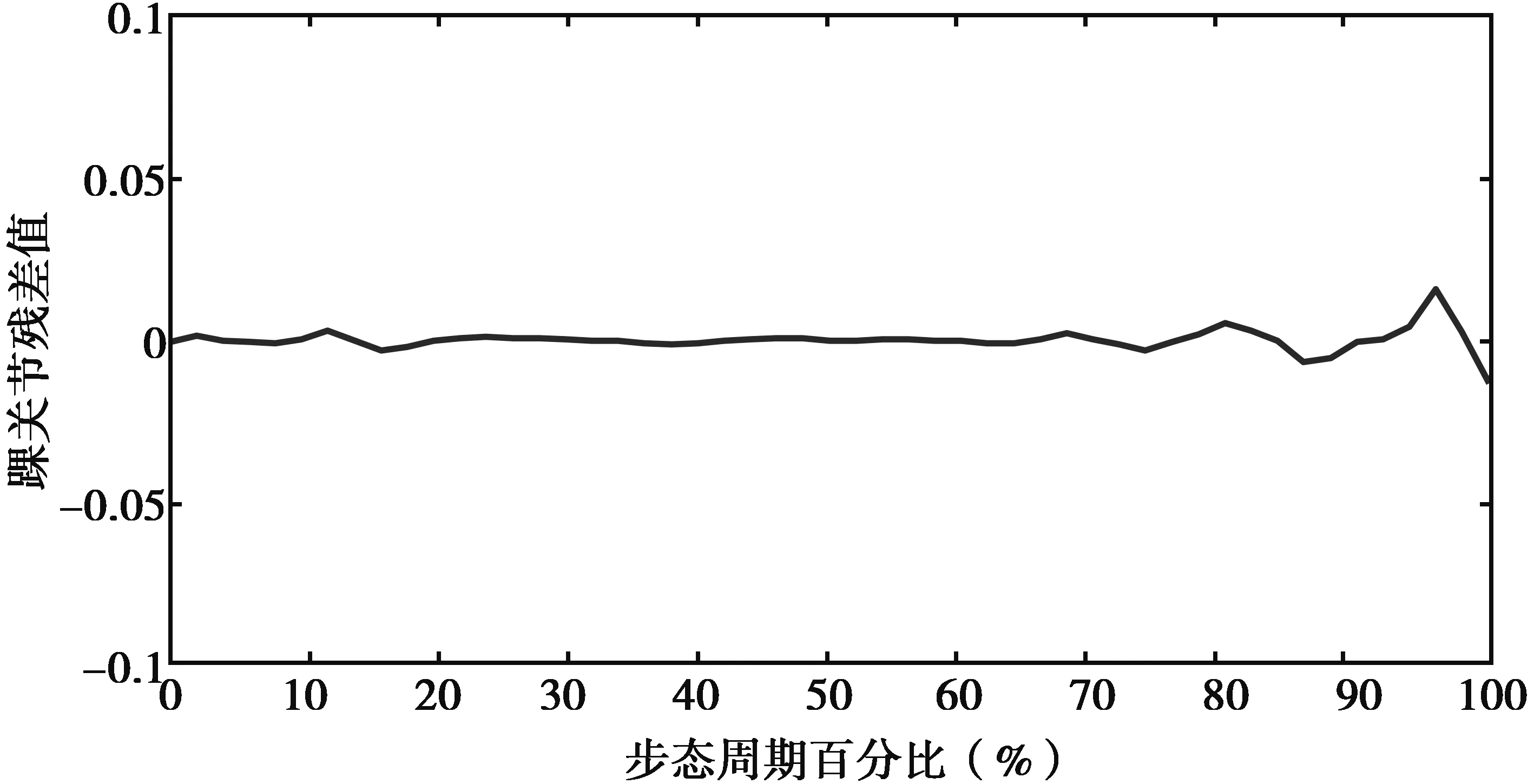
图11 踝关节拟合曲线的残差

表6踝关节残差系数值

系数项和方差确定系数标准误差标准差系数值0.173 60.999 90.999 90.069 45

从图11所示的踝关节拟合曲线的残差可以看出，拟合出来的曲线残差在负0.015与0.02之间波动，残差比较小,能符合拟合的要求.从表6所示的踝关节残差系数值可以看出，残差的标准差为0.069 45，标准误差为0.999 9，符合标准差不超过1.5，标准误差不超过1的要求.

3 实验验证

通过上述拟合曲线法构建出来的数学模型，可以得到的髋关节角度θhip，膝关节角度θknee，踝关节角度θankle的数学表达式分别为

为了验证该方法的可行性，现随机选取x等于20,60和80，带入上述髋关节、膝关节以及踝关节的数学表达式中，可以得到如表7所示的角度值.将计算出来的角度值与表8所示实验测出的角度值进行比较，可以发现两者的差值不大，所以通过上述基于最小二乘法来进行步态机器人运动轨迹辨识的方法是可行的，并且实验构建的数学模型函数相对比较精确，标准差和标准误差都较小，有利于进一步来分析与研究.

表7 建立的模型表达式计算出的值 (°)

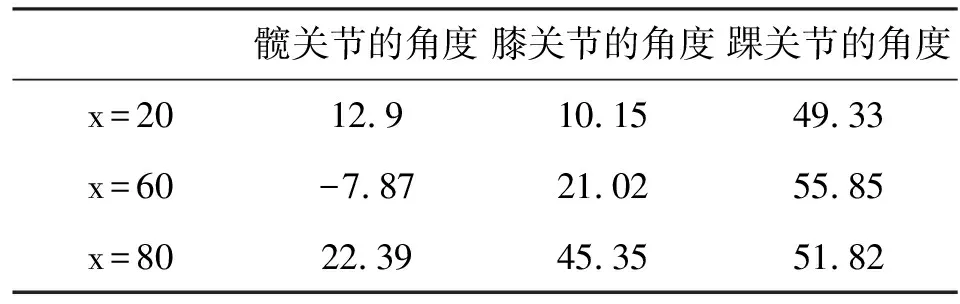
表8 实验测出的值 (°)

4 总 结

在对步态机器人运动轨迹研究的基础上，运用最小二乘法来完成其最优运动轨迹辨识.在研究之前，先对人体步态特征参数进行测量并计算关系式，再通过曲线拟合的方法，为各个运动环节的轨迹建立相应数学模型，最后得出整个运动轨迹系统的数学模型.实验结果表明，文中方法对研究步态机器人运动轨迹具有误差小并且比较精确的特点.

参考文献：

[1]贺玲玲.移动机器人空间姿态测量系统研究与设计[J].重庆工商大学学报：自然科学版,129(9):38-42

[2]朱庆保，张玉兰.基于栅格法的机器人路径规划蚁群算法[J].机器人,2005,27(2):132-136

[3]庄晓东，孟庆春，殷波，等.动态环境中基于模糊概率的机器人路径搜索方法[J].机器人,2006(21):197-199

[4]周郭许，唐西林.基于栅格模型的机器人路径规划快速算法[J].计算机工程与应用,2010,32(7):104-107

[5]唐国新，陈雄，袁杨.基于改进遗传算法的机器人路径规划[J].计算机工程与设计,2007,28(18):4446-4449

[6]周磊,王华忠.改进蚁群算法在机器人路径规划中的应用研究[D].华东理工大学,2012

[7]何娟，涂中英，牛玉刚.一种遗传蚁群算法的机器人路径规划方法[J].计算机仿真,2010,27(3):170-174

[8]冯治国，钱晋武.步行康复训练助行腿机器人系统[D].上海大学,2009

[9]NIXON M S,TAN T N,CHELLAPPA R .Human Identification Based on Gait [M].New York : Springer，2005

[10]VAUGHAN C L，DAVIS B L，O’CONNOR J C .Dynamic of Human Gait [M].Cape Town: Kiboho Publishers，1999

[11]王企远，钱晋武.步行康复训练机器人助行腿的步态规划与运动控制[D].上海大学，2011