含风力发电的电网概率潮流计算的研究

吕文婷，周雪影，徐春雷

（三峡大学电气与新能源学院，湖北宜昌443002）

含风力发电的电网概率潮流计算的研究

吕文婷，周雪影，徐春雷

（三峡大学电气与新能源学院，湖北宜昌443002）

提出了一种计算含有风电场电力系统潮流概率密度函数的方法。利用风机功率曲线的二次近似来求解风机注入电网后的功率概率密度函数。基于这种模型，考虑发电机注入功率以及负荷消耗功率具有随机性，网络的直流功率潮流也可以计算出来。以含风电场模型的IEEE14节点系统为例，得出了线路功率的概率密度函数，验证了该方法的有效性和正确性。

二次近似；直流潮流；功率曲线；概率潮流；风力发电机

1 引言

考虑各发电机注入功率的随机性，进而求出电功率网络的系统状态和功率潮流，还有母线负荷，这些都属于概率潮流。经常被运用于常规的电力系统运行中，还用于电力系统运行的短期或长期的计划中。

应用概率密度函数（PDF）或累积分布函数（CDF）的形式求解电力系统状态和功率概率潮流，需要给出PDF或CDP的输入量，系统中那些未知量会反映在计算的结果中，概率潮流还可用蒙特卡罗模拟算法得到；也可以用数学分析的方法，如卷积；或这些方法的综合。蒙特卡罗模拟的不足之处是需要进行大量的仿真，这就需要耗费大量的时间［1］，数学分析方法的不足之处就是其数学模型比较复杂，并且计算过程中用到很多近似处理，会导致计算结果不够精确，本文提出的方法将会克服这些缺点。

2 含风电场的电网

2.1 风力发电机

由于风力发电依靠的是存在很多不定因素的风力资源，风力资源的波动性可以从时间和空间的角度来分析，在固定地点的风速波动性可以从年代统计的角度来分析，或者用累积的方法，该方法可以用于潮流计算中。本文将从累积的角度来分析，把重点放在研究风速短期的变化规律上。以往在概率潮流问题中运用过风电功率积分的方法，但是却没有考虑风机的功率曲线的二次近似模型［2］。

2．2 潮流计算模型

电力系统潮流的节点的有功和无功功率方程为：

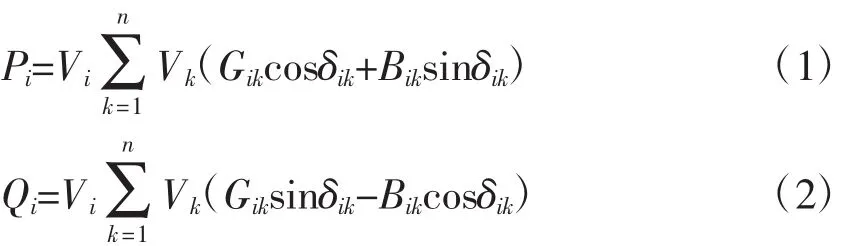
式中：Pi与Qi分别是节点i消耗的有功和无功。Vi和Vk是节点i与k节点的电压有效值，δik是节点i与k节点的电压的相角差，Gik和Bik是线路ik之间的电导和电纳。

如果各母线发出的功率（除了平衡母线）和系统中的母线负荷都已知，式（1）和（2）可以求出各节点的电压Vi和相角δi，在这种模型中，流过线路ik的有功和无功可表示如下：

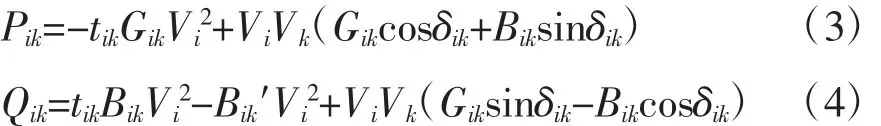
式中：tik是变压器分接头的变比（在没有分接头的情况下，tik＝1）。

由于式（1）、式（2）中的电压幅值和电压相角都是非线性的，这种基于数值分析的模型必须以一种迭代的方法为基础。如高斯-塞得维或牛顿-拉夫逊迭代法。但包含迭代的算法很长，而且在概率分析中，式（1）和（2）用线性近似处理将会更好，因此，可以用线性的输入变量代替状态变量，这样不仅可以又快又直接的解出潮流方程，还可以运用卷积技术来处理概率潮流问题。

2．3 直流潮流

在式（1）中，假设Vi＝Vk＝1，Gik＝0，并且sinδik≈δik，进而可以推出母线i的注入功率为：

式中：Xik是线路ik的电抗。所有连接母线k和i的线路功率都要附加进去，式（5）后面是矩阵形式。Y通过下式求得：

Y中对应于母线的行和列都为0，如果Y是可逆的，则δ为：

在此相关元素用相同的符号表示，Yˆ表示Y逆矩阵。由式（3）可以求解出线路ik的实际有功为：

矩阵H（ik）j表示母线j对线路ik的出力，如果母线j是平衡母线，则H（ik）j＝0。因此，要求出流过线路ik的实际功率，就要计算式（8），式中H（ik）j取决于系统网络的分布结构。

因为已发出的功率和母线负荷具有随机性，就不能赋予确定值，用它们的PDF代替。求解线路ik中的实际功率有两种方法：一种是把常量和PDF所描述的变量值相乘，这个过程可以通过改变PDF中的变量值来得到另一个PDF来实现；另一种是增大PDF所描述的变量值，这个过程可以通过各个PDF卷积而得到期望的PDF来实现。

3 求解PDF

PDF的求解过程要考虑一些因素，如要变动PDF时，就要清楚怎样实现各个变量的变化，利用卷积或者傅立叶变换。

3．1 变量的改变

如果一个变量y是另一个变量x的函数，即y＝g（x），若x的PDF已知，那么改变x的值相应地可以求出y的PDF,当g是单调函数时，在此用fx（x）表示x的PDF，则y的PDF［3］为：

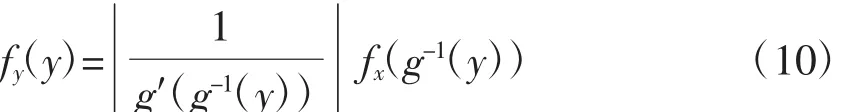
g-1为逆函数，g′为导函数。如果y＝ax中，a为常数，用它来求y的PDF可以用下式：

3．2 卷积

若x与y是相互独立的，它们的PDF分别为fx（x）与fy（y），若独立变量z＝x＋y，那么z的PDFfz（z）可以由fx（x）与fy（y）的卷积求得：

3.3 傅立叶变换

当用式（10）求解计算量很大时，也可以用其它一些方法来求解，如fx（x）与fy（y）的卷积，即fx（x）*fy（y），如傅立叶变换方法可表示为：

分别将式中fx（x）、fy（y）和fz（z）进行傅里叶变换得到Fx（ω）、Fy（ω）和Fz（ω），式（11）可以看出fz（z）可以通过对Fz（ω）进行反傅立叶变换求得。

4 注入功率的PDF

注入功率包括除风机以外其它发电机以不同形式注入电网的功率。为了引出概率潮流中的功率，可以运用一个不连续的分布［4］，该分布中，每个注入功率都有对应的有限个输出量，而且每个输出量都在一定程度上修正过。当不考虑风机功率时，则注入功率的PDF为：

式中：x表示注入功率，ai表示功率等于ci的概率。

5 母线负荷的PDF

母线负荷可以用一个正态分布表示［4］，其PDF为：

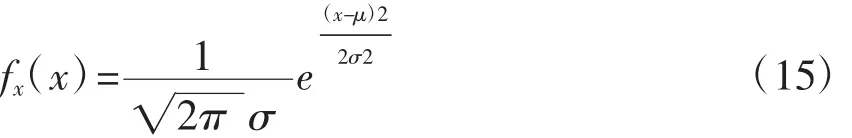
式中：x表示母线负荷，μ和δ2表示该分布的期望和方差。如果母线负荷没有正态分布的统计性特征，就用第4部分描述的不连续分布来表示。

6 风机注入功率的PDF

研究一个包含风机的电力系统时，要进行一系列的计算，这些计算是基于目前对风电场特征的研究完成的，例如风速的PDF或平均值，或者发电机的功率曲线，这些都是由仿真完成的。本文提出，风速的平均值和风机的型号与风机注入功率的PDF之间存在一种解析关系。

6.1 风机的功率曲线的二次模型

风机的功率曲线的函数模型可以分为4个不同的部分［3］：

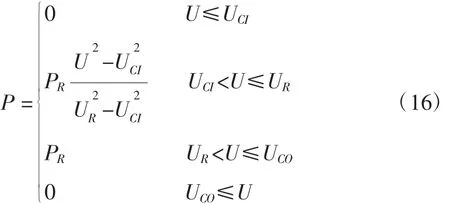
式中：PR是额定功率，UR是额定风速，UCI是切入风速，UCO是切出风速，式（14）就是功率曲线的二次模型，图像如图1所示，图中把直接由制造商给出的曲线与二次模型得到的曲线作了比较。它表示一个额定功率为1.8MW的vestas V100风力发电机。用二次近似模型可以求得功率的PDF。

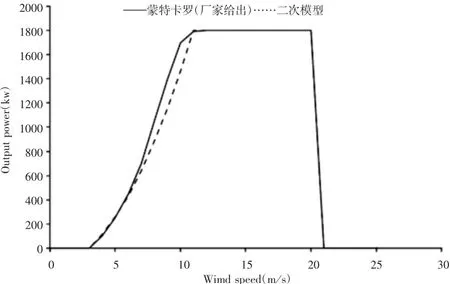
图1 两种方式的曲线

6.2 用威布尔分布描述风速的PDF

一般在固定地区的风速的PDF服从威布尔分布［5］，在此用而参数的威布尔分布表示，它密度函数为：

式中：常量C和k是威布尔分布的尺度参数和形状参数。C和k可以由LegendreΓ分布求得的风速分布中的μU和求得［6］。Legendre分布可以用来转换，令k＝2时，可以求得风速的平均值。

6．3发出功率的PDF

要求出风机输出功率的PDF，就要求出变量P＝g（U）的PDF［7］，fU（U）表示U的PDF，当g为单调函数时，由式（9）可得：

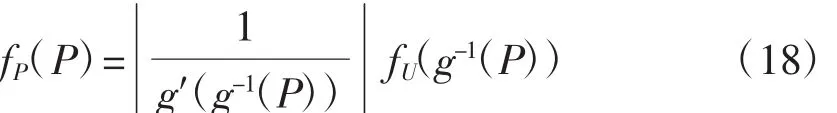
现在把式（14）中4个不同部分分别单独分析：

（1）第一部分和第四部分：显然发出功率为0有两部分构成：

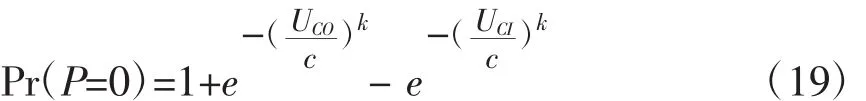
（2）第二部分：发出功率在0和PR之间，利用式（17），功率的PDF就可以求解出来：

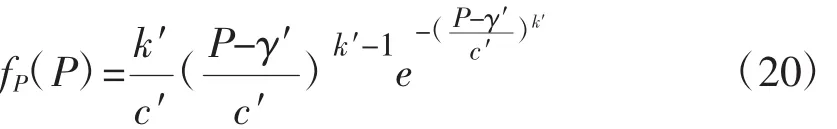
该式与6．2中描述的威布尔分布类似，式中c′、k′还有γ′为：

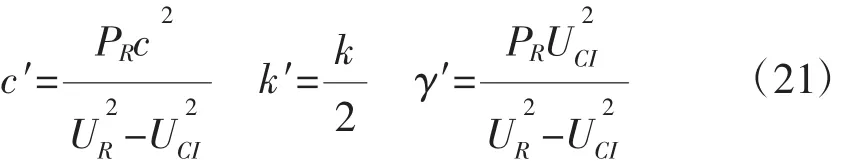
（3）第三部分：发出功率等于PR的概率为：

（4）总结：综合上面的讨论，用二次近似模型求得风机发出功率的PDF为：

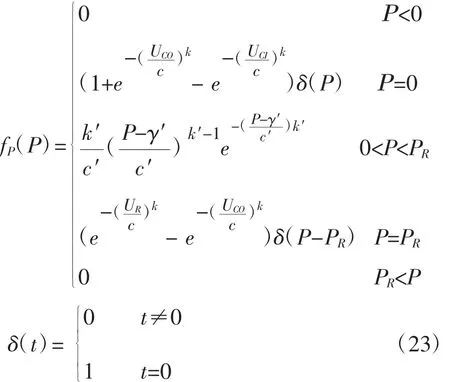
7 风电场的注入功率

要求出整个风电场注入功率的PDF，就要研究风速和风机的关系，若在风电场中，各风机的相关性很高（相关系数大于0．8）［8］，那么整个风电场就能等效为第6部分描述的风机模型，若风电场中风机的台数为n，那么只需把式（15）中的PR换成nPR。

如果各风机的相关性很低，这种情况可参考其他文献［9］。

8 实例分析

综合考虑上述各因素，用文中提供的方法求解电力网络的功率潮流，首先根据式（23），从风速参数开始，为了简化计算，把风机的PDF当作矢量。再用式（9）求解流经各线路的功率与其端点母线发出和消耗的功率的关系，利用式（11）转换所有的PDF时，要考虑各功率的相关系数。要进一步修正PDF，就要用到式（12）进行两两卷积。最后把得到的结果与用蒙特卡罗模拟仿真的结果进行对比。

8．1 IEEE 14节点系统

用IEEE14节点系统验证本文方法，在母线3上注入风电场，母线1为平衡母线。因为本文的目的不是研究风电场内部的运行特性而是要从数据方面分析整个风电场对电力网络的影响，所以对于母线3，可把风电场等效为风机。该系统各参数引用文献[10]。

用Matlab软件仿真，蒙特卡罗模拟也可以用Matlab仿真，仿真结果如图2、图3所示。

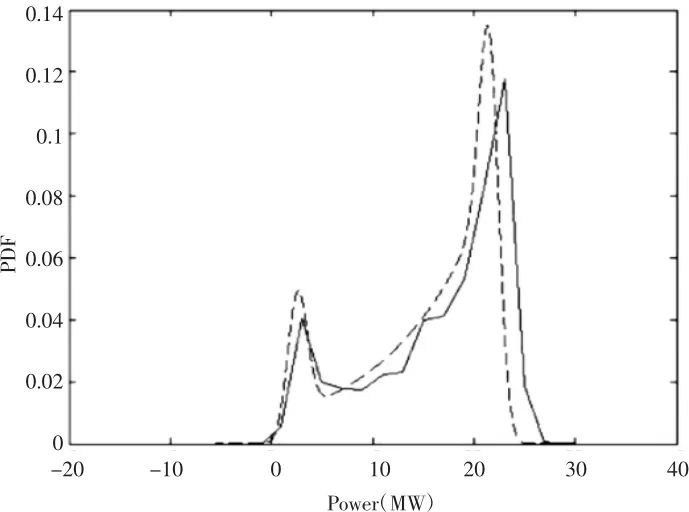
图2 流经线路2-3的功率的PDF

图3 流经线路2-4的功率的PDF

观察图2和图3，很显然2-3,3-4这两条线路功率的PDF受风电场的影响很大，因为它们离风电场最近。

9 结论

把本文提出的方法（虚线）与蒙特卡罗模拟（实线）的进行对比可知，当引进风机时，文中提出的方法可以合理地模拟电功率网络的概率潮流，而且风机的加入对网络的影响也可通过比较装设风机前后求得的功率潮流的PDF来分析。加入风电场后，流经不同线路功率的概率都大于加入风电场之前的值。与蒙特卡罗模拟方法进行对比，显然本文提出的方法不仅省时且更为精确，还避免使用复杂的数学模型。

［1］董 雷，程卫东，杨以涵等．含风电场的电力系统概率潮流计算［J］．电网技术，2009，33（16）：88-91．

［2］N．D．Hatziargyriou，T．S．Karakatsanis，and M．Papadopoulos．Probabilistic load flow in distribution systems containing dispersed wind power generation．IEEE Trans．Power Syst，1993，8（1）：159-165．

［3］R．Pallabazzer．Evaluation of wind-generator potentiality．Solar Energy，1995，49-59．

［4］R．N．Allan，C．H．Grigg，and M．R．G．Al-Shakarchi．Numerical techniques in probabilistic load flow problems，Int．J．Numer．Meth．Eng．，1976，10：853-860．

［5］王晓龙，韩富春，田 亮，等．含风电场电力系统概率潮流计算［J］．水电能源科学，2012，30（10）：189-191．

［6］IEC 61400-1：Wind Turbine Generator Systems．Part 1：Safety Require-ments，IEC Standards，1994．

［7］H．Pham，Handbook of Engineering Statistics．New York：Springer，2006．

［8］邓 威，李欣然，徐振华，等．考虑风速相关性的概率潮流计算及影响分析［J］．电网技术，2012，36（4）：45-49．

［9］A．Feijóo and R．Sobolewski，Simulation of correlated wind speeds，Int．J．Elect．Energy Syst．，2009，2：99-106．

［10］Daniel Villanueva，José Luis Pazos，and Andrés Feijóo，Probabilistic Load Flow Including Wind Power Generation．IEEE Trans．Power Syst，2011，26（3）：1659-1667．

下期要目

● 基于模糊PI控制的双馈风力发电机空载并网控制策略

● 三电平PWM整流器中点平衡控制技术的研究

● 加热炉炉温PID模糊控制方法的研究

● 永磁同步电机闭环弱磁的研究

● 中点活箝位三相五级逆变器研究

● 基于PROFIBUS总线技术的智能从站设计

● 基于煤矿井下综采工作面机电设备集中控制系统的设计

Research on probabilistic power flow containing wind power generation

LV Wen-ting，ZHOU Xue-ying，XU Chun-lei
（Electrical Engineering＆Renewable，China Three Gorges University，Yichang 443002，China）

A calculation method of probability density function containing wind farm power system is proposed. taking into account the wind power generation.The power probability density function after fan injecting into power grid is solved by using a quadratic approximation of power curve.Based on this model,considering the randomness of generator power injection and load consumption power,DC power tide of network can be calculated.Taking the IEEE14 node system model of wind farms for example,the probability density function of line power is obtained. The validity and correctness of method are verified.

quadratic approximation;DC power flow;power curves;probabilistic power flow;wind generator

TM614

A

吕文婷（1988-），三峡大学电气与新能源学院，电力系统及其自动化专业硕士研究生，研究方向为电力系统分析控制与保护。

2013-04-26

1005—7277（2014）01—0051—05