金融数据的极端风险研究及实证分析
2014-08-08孙丽莉刘琼荪
孙丽莉, 刘琼荪
(重庆大学 数学与统计学院,重庆 401331)
1970年以后,金融资产价值的暴跌开始受到广大的投资者乃至各金融监管机构的特别关注。非参数方法对极端风险的估计是基于极值理论(EVT)[1]发展而来的。极值理论仅研究收益率序列的尾部分布情况,关心特殊情况发生极端事件的概率。极值理论已广泛应用于金融市场的风险评估、通信业的事故预测以及海洋水文的风险防范等诸多领域,因此研究极值理论及其应用具有十分重要的意义。
1988年,极值理论首次应用于金融领域,研究了拉美汇率分布的特征。McNeil(2001)探讨了如何利用极值理论估计损失分布的尾部大小和金融时间序列的风险测量 。王旭、史道济(2001)将极值理论用于日元对美元汇率的实证研究;潘家柱和丁美春(2000)讨论了广义帕累托分布的一些性质,并对上证指数和深证指数等收益率进行了分析等。Heideman(1978)对墨西哥湾飓风发生频次的规律性进行了统计研究,结果表明:墨西哥湾飓风的发生频次可以用Poisson点过程来模拟。Feller(1957)首先提出了复合极值概念。刘德辅和马逢时(1980)在此基础之上推导了复合极值分布的显性表达式并成功地应用于波高统计分析中。随后,相继研究了适用于美国墨西哥湾、大西洋沿岸飓风海域的Poisson-Weibull复合极值分布。
在极值理论已有成果的基础上,研究了两分布融合的极值模型,并将其应用于金融风险管理中;结合广义帕累托分布,赋予变量新的意义,引入Poisson-GP复合超阈值模型,进行投资损失预测;并对上证指数1996-2013年间的日收益率序列进行了实证分析。
1 广义帕累托分布及参数估计
1.1 广义帕累托分布[2]
假设某金融资产的损失(常用资产负收益表示)序列{Zt}具有分布函数F(x),对于给定的阈值u,定义Fu(y)为超额损失分布,即随机变量Z超过阈值u的条件分布函数,定义为
Fu(y)=P(Z-u≤y|Z>u),y≥0
(1)
由条件概率公式,可以得到:
(2)
则F(z)=Fu(y)(1-F(u))+F(u)。
定理(Balkema,De Haan (1974),Pickand (1975)) 对于充分大的阈值u,存在一个分布函数Gξ,σ(y),使得一族分布F(几乎包括所有的常用分布)的超额损失分布函数Fu(y),收敛于Gξ,σ(y),即:
(3)

称分布函数Gξ,σ(y)为广义帕累托(Pareto)分布。其中,σ,ξ分别表示广义帕累托分布的尺度参数和形状参数。通常称1/ξ为尾部指数,其大小能够反映分布的尾部形状。根据ξ的不同取值,GPD对应着不同的分布形式。当ξ>0 时,是通常意义下的Pareto分布,它具有厚尾的特征,在金融时间序列分析中备受关注;当ξ=0时,GPD则对应于指数分布,它具有正常的尾部;而ξ<0时的GPD被称为Pareto Ⅱ型分布,它的尾部较薄。如图1所示。

图1 广义Pareto分布在σ=1,ξ取-0.3,0,0.3的图形
1.2 GPD的参数估计
由公式(3)可以得到广义的Pareto分布的概率密度函数gξ,σ(y):
(4)
需要对式(4)的参数ξ和σ进行估计。
由式(4)和给定的符合广义的帕累托分布的样本观测值(y1,…,yn),则对数似然函数l(ξ,σ|z)可表示为
(5)
1.3 风险值VaR[3]和期望损失ES

(6)
这样,对于某个给定的置信水平p,由式(6)以及VaRp=F-1(p)可以得到:
(7)
并根据ESp(X)=E[X|X≥VaRp]得到:
(8)
2 Poisson-GP复合超阈值分布
2.1 Poisson-GP复合超阈值分布
在气象、水利等领域广泛应用的复合极值模型的研究基础上,将其应用于金融风险管理领域。结合Poisson分布与广义帕累托分布(GPD),赋予变量新的意义,构造Poisson-GP复合超阈值模型[4]。


对复合极值分布中的随机变量δ和N分别表示每年所有的超阈值δ和每年所有超阈值的个数Nu,则假设随机变量δ的分布为GPD:

不妨设随机变量Nu服从参数λ的Poisson分布,随机变量η和ζ的定义不变,从而构造随机变量ζ的分布函数——Poisson-GP复合超阈值分布为
(9)
分布在广义帕累托分布的基础上引入了新的参数,丰富了模型的内涵,用参数λ的Poisson分布来表示每年极端事件发生次数的分布,即每年极端事件约平均发生λ次,有助于极端风险的全面研究。
2.2 复合超阈值分布的参数估计
由式(9),对Fζ(x)求导,得密度函数:
(10)
由此建立对数似然函数:
(11)
在确定了阈值u的基础上,根据式(11)进行极大似然估计:
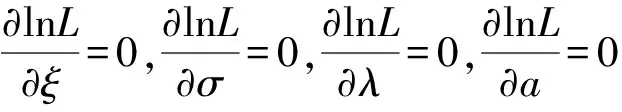
3 阈值u的确定[6]
如何确定阈值u是POT模型中的一个关键问题,也是一大难点。De Vries,Danielsson et al(1997)和Dupuis(1998)给出了Hill图法,但此方法需要从图中观察变点来选取阈值,属于定性的方法,存在较大的误差。现主要讨论以下的定量方法。
在样本容量n有限的情况下,将样本决定的厚尾分布概率密度图的尾部与正态分布进行比较,有如下两种情况:
(1) 厚尾分布概率密度图的尾部全部高于正态分布概率密度图的尾部。
(2) 厚尾分布概率密度图的尾部大部分高于正态分布概率密度图的尾部,然而在某些小区域,前者低于后者,即厚尾分布概率密度图与正态分布概率密度图高低交错。
为此将样本标准化后的厚尾分布与标准正态分布作比较,使得在某一点厚尾分布的尾概率与标准正态分布的尾概率之差达到最大,并且把达到优化目标的这一点认为是选取次序统计量的阈值,从而得到用于厚尾指数估计的次序统计量。
记样本标准化后的逆序统计量记为,假设存在常数u,X(k+1) (12) 由式(12)可选取POT模型的阈值u。 采用GPD和Poisson-GP复合超阈值两种分布下的POT模型进行了实证对比研究。主要研究了上海股票市场指数的尾部特征。数据源自上证指数1996-12-16至2013-04-15的收盘价格。假设{Pt}表示金融资产价格的时间序列,采用对数收益率序列Rt=log(Pt)-log(Pt-1)。 选取上证指数1996-12-16至2013-4-15的日收益率序列{Rt},样本容量3 947。采用R软件画出日收益率序列的图形,如图2所示。图形显示了该金融数据具有较强的极端波动情形;画出上证指数日收益率的密度估计曲线,并与正态分布的概率密度函数进行对照,如图3所示。显示了上证指数日收益率序列与正态分布相比,具有明显的尖峰厚尾特征。 此外,用R软件计算其偏度(Skewness)系数值为-0.207 7,系数为负表明该序列具有左端拖尾的特征;峰度(Kurtosis)系数值为4.367 4,明显大于标准正态分布的K值3,说明该时间序列的凸度比正态分布要高。用正态性W检验法的p值小于2.2e-16,非常接近零。因而,表明拒绝该时间序列的正态性假设。 图2 上证指数日收益率序列{Rt}图形 运用R软件求解最优化问题(12),得到阈值u为0.021 2,且上证指数的日收益率序列中超阈值u的样本为312个。 运用R软件和极大似然估计方法进行参数估计。计算结果如表1所示。 表1 广义Pareto分布参数的极大似然估计 分别画出GPD以及Poisson-GP复合超阈值分布的拟合曲线,如图4和图5所示,显示两种分布对上证指数日收益率的右端尾部均具有较好的拟合效果。 图4 拟合GPD以及经验分布曲线 图5 拟合Poisson-GP以及经验分布曲线 (1) 将GPD的参数带入式(7)和式(8),分别选取p=0.95和p=0.99,计算出VaRp和ESp的估计值,见表2。 表2 POT模型中p=0.95 和p=0.99时的VaRp和ESp VaR0.95=0.026 4表示有5%的可能上证指数日收益率高于0.026 4,VaR0.99= 0.045 8表示有1%的可能上证指数日收益率高于0.045 8。ES0.95=0.039表示在给定日收益率高于0.026 4的条件下,上证指数的平均收益率为0.039,同理ES0.99= 0.062 5指在给定日收益率高于0.045 8的条件下,上证指数的平均收益率为0.062 5。 (2) 新引入的Poisson-GP复合超阈值分布同样具有很好的拟合效果,并且其参数λ也具有现实意义,通过参数λ的估计结果可以判断,每年大约有18个超阈值,也就是说每年大约发生18次极端风险。 参考文献: [1] 张国辉.极值理论及其在风险价值的应用[D].浙江:浙江大学硕士论文,2003 [2] 潘家柱,丁美春.GPD分布模型与股票收益率分析[J].北京大学学报:自然科学版,2000(2):295-306 [3] 郑文通.金融风险管理的VaR方法及其应用[J].国际金融研究,1997(2):58-62 [4] LIU J,SHI D J,WU X R.Estimation of Poisson-Generalized Pareto Compound Extreme Value Distribution by Probability-Weighted Moments and Empirical Analysis[J].Transactions of Tianjin University,2008,14(1):50-54 [5] 刘晶,吴新荣,李素红.Poisson-Gumbel复合极值分布的参数估计[J].统计与决策:理论版,2007(9):17-19 [6] 史道济,张春英.尾部指标估计中的阈值选择[J].天津理工大学学报,2002(6):78-81
4 实证分析
4.1 上证指数的尾部特征研究

4.2 确定POT模型中的阈值u
4.3 GPD和Poisson-GP合超阈值分布的参数估计

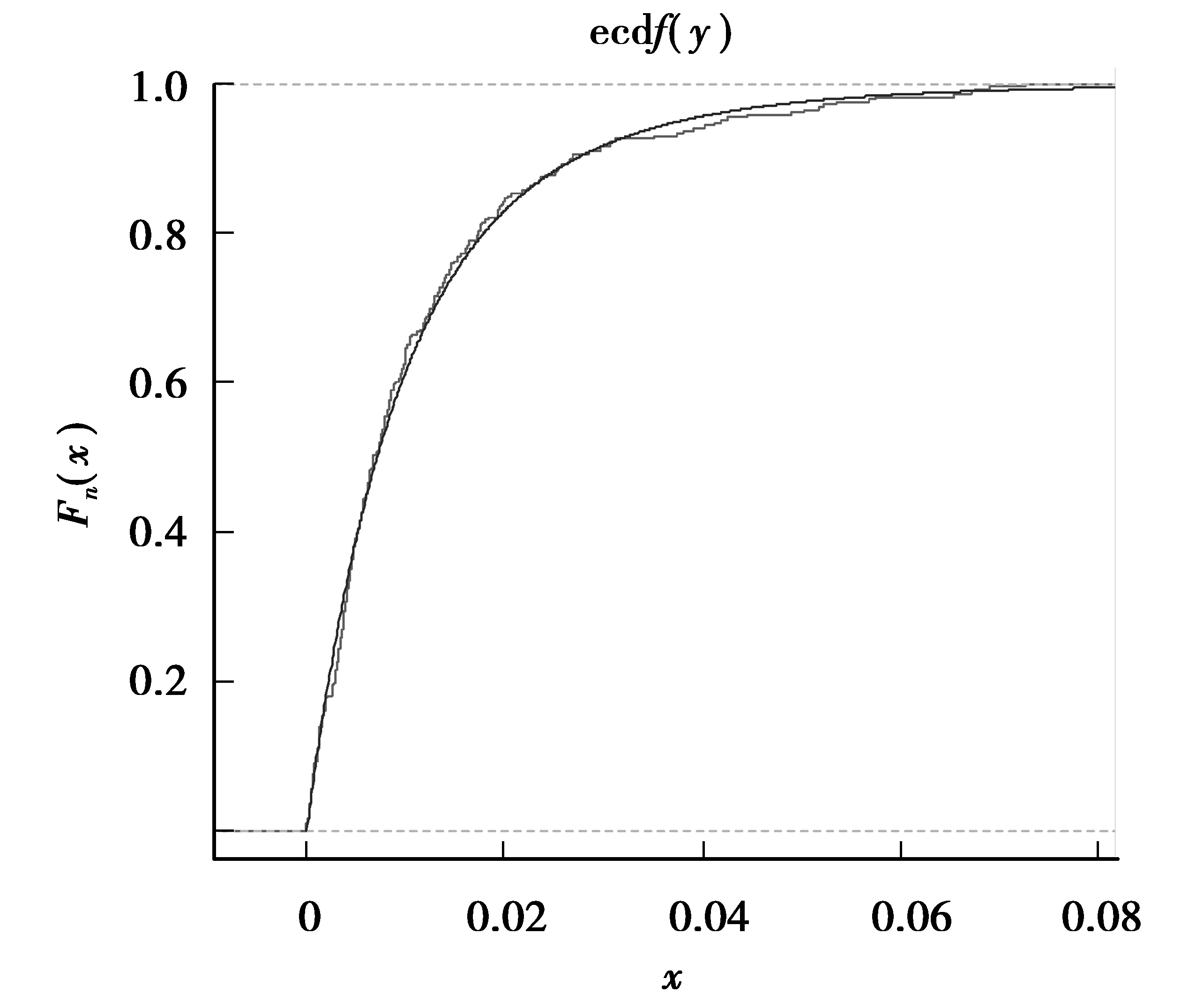

4.4 结果分析

