基于数值模拟气液比对豆胶气泡雾化的影响1)

花 军 张文程 贾 娜 Sheldon Q.Shi

(东北林业大学，哈尔滨，150040) (深圳市特尔佳科技股份有限公司) (东北林业大学) (美国北德州大学)

豆胶(即豆基蛋白胶)在环保方面的优势，使得国内外许多学者研究对其进行改性后应用在人造板中，以避免甲醛造成的环境问题［1－5］。但目前的研究发现，豆胶的高黏度特性及非牛顿流体特性很难适应纤维板(刨花板)生产的施胶工艺［6］;其改性后得到的豆胶黏度，最高可达20 mPa·s［7］，国内纤维板(刨花板)生产线现有的施胶方式无法实现其雾化。因此，研究如何能使这种具有高黏度、非牛顿流体特性的豆胶雾化，成为豆胶扩展应用的核心问题。

豆胶在雾化过程中的工作参数主要包括:豆胶物性参数、气体注入速度、液体注入速度、气液比(气液质量流量比)、工作压力等［8］。气液比对豆胶雾化的影响是关键因素［9］。笔者拟采用数值模拟的方法，通过改变气液比，对豆胶与空气在喷嘴内部的流动情况进行数值模拟，研究气液比对豆胶雾化的影响;并对豆胶在喷嘴出口下游的雾场进行仿真，验证最佳气液比的正确性。

1 数值模拟的方法

气泡雾化的过程分为两部分:气液在喷嘴内部的混合流动与液体在喷嘴出口下游的雾化。气泡雾化效果好的前提，是必须保证气液在喷嘴内部的混合情况良好。当其他条件不变，单独改变气液比进行雾化时，首先发生改变的是喷嘴内部的流动情况;流动情况发生改变，直接导致喷嘴出口的压力、速度等数据的变化，这些数据的变化最终直接影响雾化效果。研究气液比对豆胶雾化效果的影响分两步:一是研究气液比对气液在喷嘴内部流动情况的影响，二是研究喷嘴出口数据对雾化效果的影响。模拟时采用的方法为:通过喷嘴内部流动情况的数值模拟，分析气液比对流场分布的影响，并得到进出口的速度及压力等数据;通过对数据的理论分析计算，研究气液比对相关参数的影响，得出最佳气液比;其后，通过喷嘴下游雾场的仿真，对得出的最佳气液比进行仿真验证。

模拟时，喷嘴内部流场的数值模拟，采用的模型为多相流混合模型;喷嘴下游雾场的仿真，采用的模型为离散相模型;压力和速度的耦合均采用Simple方法。一般试验研究时，理论上气泡雾化喷嘴存在一个最大气液比，约为0.1;当气液比过大，会影响模拟结果的准确性;模拟选取的气液比均小于0.1［10］。气液比的改变，通过固定气体流量不变，单独改变豆胶流量来实现。

2 不同气液比下的混合数值模拟

2.1 混合模拟条件

模拟所采用的材料、喷嘴结构、数值模拟的三维模型及求解器工作条件均与文献［9］的混合模拟相同。为了提高模拟效果，本次模拟采用气液比分别为 0.04、0.05、0.06、0.08 进行计算，其对应的豆胶流量分别为 0.70、0.56、0.47、0.35 m3/h;针对文献［9］中出现的局部湍流过强造成的局部静压为负的问题，将空气流量固定为25 m3/h。为了提高网格划分质量，本次模拟对网格采取自适应网格划分。

2.2 混合模拟结果的分析方法

进行不同气液比条件下，豆胶与空气的混合数值模拟，是为了寻找最佳气液比。最佳气液比的条件，是在满足雾化良好的情况下，雾化总能量高，气耗量低;模拟得到的结果，是不同气液比下的压力场分布图、速度矢量场分布图、组分体积分数场分布图。从图中可以得到进出口压力及出口速度等一些数据，针对这些数据分析最佳气液比值。

2.2.1 流场分布图

流场分布图，主要是用来显示豆胶与空气的混合情况。不同的流场分布图，可以看到不同的混合情况，得知其混合的效果。流场分布图，主要通过压力场分布图、速度矢量场分布图、组分体积分数场分布图体现。其中，压力场分布图中，除满足压力从进口到出口逐渐减小之外，在通气孔处，空腔的压力应大于中心管中的压力，使得气体进入中心管与液体混合。速度矢量场分布图，应满足速度逐渐增大的趋势;组分体积分数场分布图中，豆胶从喷嘴进液口到出口应逐步均匀的减小，并被包围在气体之中。因此，只有满足这3个图的条件才能说明，豆胶与空气进行了很好的混合。

2.2.2 出口的数据

气泡雾化喷嘴，实现液体雾化的2个条件分别是［11］:

(1)气泡在出口处，由于内外的极大压力差，克服液体的表面张力，破裂，爆炸成小液滴。

(2)气泡在迅速扩大时把液体压成液丝，当气泡爆炸时，其释放的能量克服液体的黏性力，使得液丝雾化成小液滴;在不断的爆破中，液滴还将因能量的冲击而雾化成更小的雾滴。

豆胶的表面张力远小于水的表面张力，克服表面张力实现雾化是可行的。假定单位时间内雾化的豆胶的体积定义为VL，则雾化过程中所需要的雾化空气的质量(Mg)为:

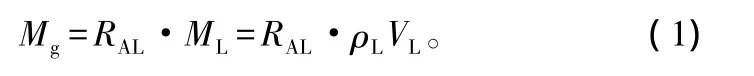
式中:RAL为气液比;ML为雾化豆胶的质量;ρL为雾化豆胶的密度。

雾化过程中，作用在液体上的总能量包括3部分:液体的压力势能(E1)、气体的动能(E2)、气体的压力势能(E3)。计算式见式(2)～式(4)［12］。

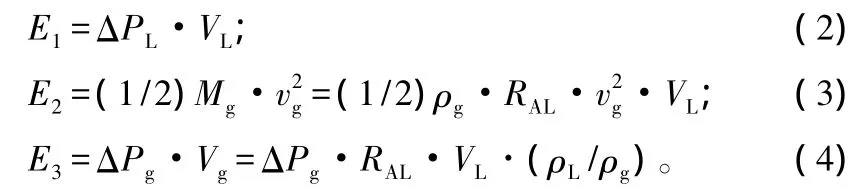
式中:ΔPL为单位面积上豆胶的进出口压力差;vg为空气出口速度;ρg为空气的密度;ΔPg为单位面积上空气的进出口压力差;Vg为空气的体积。

计算三部分能量，得雾化总能量(E)为:

通过模拟结果中提供的出口数据，可得不同气液比条件下的雾化总能量。当不同气液比条件下的混合模拟所得流场分布图都显示混合良好时，通过比较雾化总能量的数据可得出最佳气液比;雾化总能量越高，雾化越好。

2.2.3 气耗量

气耗量，即雾化液体时所消耗的气体量，是评价雾化成本的关键因素之一。模拟所设定的气体流量为固定值。当选择不同气液比，即液体不同流量时，意味着液体流量越高，其气耗量越低;液体流量越低，其气耗量越高;气耗量与气液比成正比。在分析模拟结果时，气耗量是必须考虑的参数。

2.3 混合模拟结果

分别对豆胶与空气在气液比分别为0.04、0.05、0.06、0.08 的条件下进行混合数值模拟计算，得到它们的压力场分布图、速度矢量场分布图、组分体积分数场分布图。

2.3.1 压力场模拟结果

从图1可看出，每个气液比下的压力场均能满足压力场要求的基本条件，压力的变化符合伯努利方程。从压力降低情况看，各自的压力降低的次数与频率都比较适中，区别在于压力改变的区域及大小不同。喷嘴出口的静压皆为0。豆胶从进口到出口的压力差分别为 0.756、0.643、0.595、0.451 MPa，空气从进气口到出口的压力差分别为0.567、0.547、0.506、0.406 MPa，它们都随着气液比的增加而减小。

2.3.2 速度矢量场模拟结果

从图2可看出，每个气液比下的速度矢量场，均能满足速度矢量场要求的基本条件。从各图的速度变化情况看，气液比在 0.05、0.06 时，速度变化比较均匀，流动情况较好。不同气液比下的出口速度分别为201、172、141、112 m/s，速度随着气液比的增加而减小。

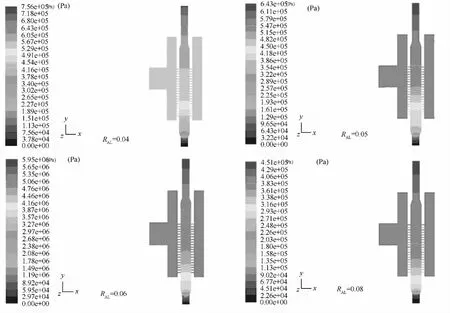
图1 压力场分布图

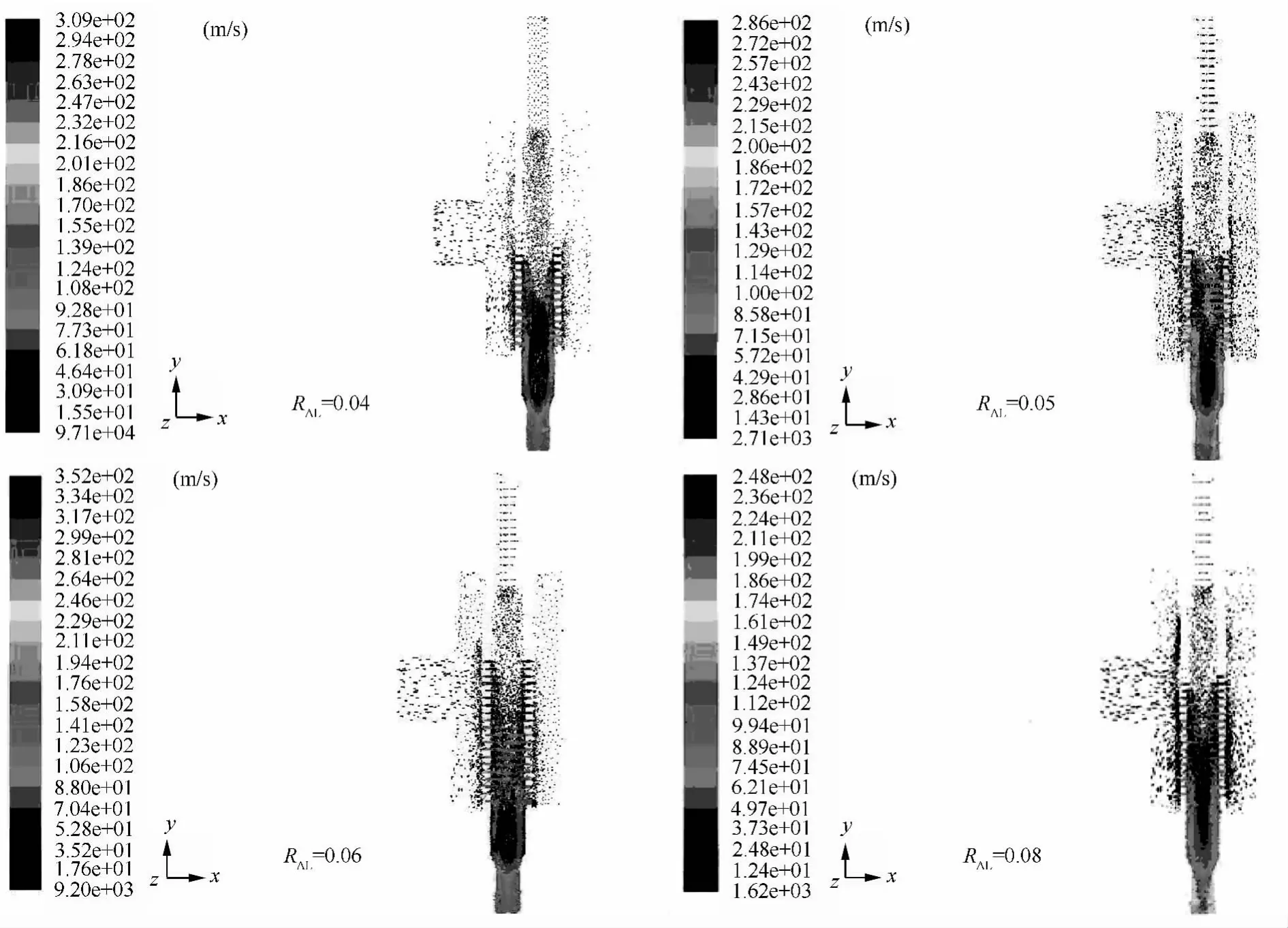
图2 速度矢量场分布图

2.3.3 组分体积分数场模拟结果

从图3可看出，每个气液比下的组分体积分数场，均能满足要求的基本条件。当气液比为0.05时，明显液体流量分布的不够均匀，从上到下的变化比较明显;气液比为0.08时，液体虽分布均匀了，但有部分区域流动不够合理，离出口更近的地方的体积却比远的地方大，这是不足的地方;气液比为0.04和0.06时的流动情况较为合理。

图3 组分体积分数场分布

2.3.4 混合模拟结果

2.3.4.1 流动情况

从图1～图3中可看出，不同气液比豆胶与空气混合情况都存在一些差异。原因主要有两方面:一是豆胶属于非牛顿流体，在不同的气液比下，随着剪切速率的变化，其黏度也发生变化，部分区域流动情况产生区别;二是小气液比能较好的形成气泡流动，形成气泡的速度较慢，但气泡的总能量没有大气液比的能量高，造成的气泡碰撞及破裂情况不同，这也是局部存在差异的原因。总体看，气液比为0.04和0.06时，豆胶与空气在喷嘴内部的混合情况，优于其他气液比条件下的混合情况。

2.3.4.2 总能量的计算

假定单位时间内雾化豆胶的体积均为1 m3，对不同气液比下的雾化总能量及气耗量进行计算(见表1)。由表1可见，雾化总能量随气液比的增加而降低，气耗量随气液比的增大而升高。气液比为0.04 时，雾化总能量最高达 8.50×105J，气耗量最低为46.0kg;气液比为0.08时，雾化总能量最低为5.10×105J，气耗量最高为 92 kg。

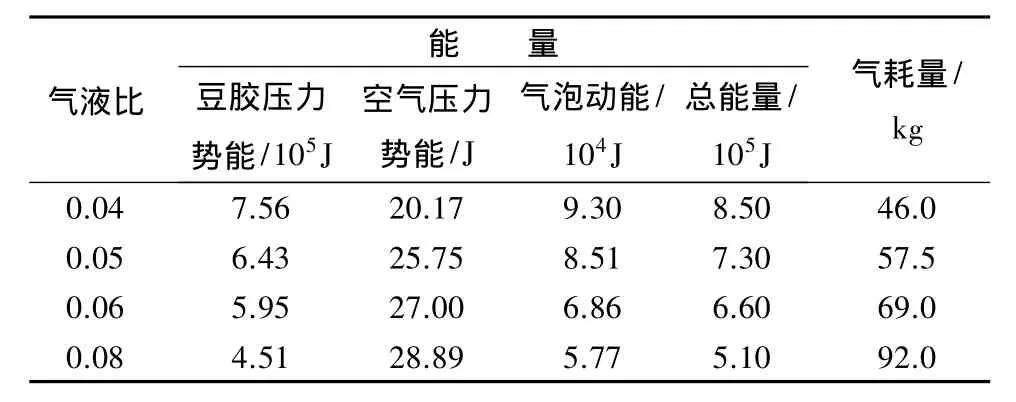
表1 不同气液比下的雾化总能量

2.3.4.3 最佳气液比的确定

文献［9］进行的气液比为0.07时的模拟结果，相对于此次模拟的结果较差;比较其他四组，气液比越低，气耗量越低，则气液比为0.04时气耗量最低。图3所示，当气液比为0.05和0.08时，气液分布显然没有另两组好，造成流动不均匀，施胶量不能保持一致，导致不利于在雾化施胶系统中的使用。对其他两组进行对比分析，当气液比为0.04时，气耗量最低，豆胶与空气在喷嘴内部的混合情况较好，雾化总能量显著高于其它组;因此，在该模拟条件下，这种结构喷嘴的最佳气液比为0.04。

3 仿真验证

仿真验证，是以不同气液比的混合数值模拟得出的出口速度、压力等数据为模拟条件，进行喷嘴下游雾场的数值模拟。分析模拟结果直接得出最佳气液比，验证与混合模拟得到的理论最佳气液比值是否相吻合。仿真时采用的模型为离散型。

3.1 离散型模拟条件

模拟时，先用k－ε湍流模型对连续相空气进行模拟，当迭代收敛之后，再加入离散相豆胶，对其进行计算。雾化所用模型为wave破碎模型，颗粒射流的模型为气泡雾化喷嘴模型。雾场模型采用结构化网格划分，网格数为21 285，划分好的网格如图4所示。材料的选择与混合模拟时相同，进口速度及质量流量等条件见表2。

表2 不同气液比下的进口速度及质量流量

图4 喷嘴出口下游雾场及截面网格划分示意图

3.2 离散型模拟结果

以混合数值模拟得出的出口数据为条件，对喷嘴出口下游雾场进行离散型数值模拟(颗粒粒径分布图见图5)。从图5可见，不同气液比，雾化颗粒的雾炬锥角分别为 35°、31°、33°、31°，雾化颗粒的粒径分别为 29、51、73、66 μm。

图5 不同气液比雾化粒径分布图

验证气液比是否为最佳气液比的关键，是在最佳气液比下的雾化效果最好;雾化效果最好的直接体现，是雾炬锥角大，雾化颗粒直径小。上述模拟结果，当气液比为0.04时，雾炬锥角最大为35°，雾化颗粒直径最小为29 μm;说明，0.04为最佳气液比，与理论分析的最佳气液比相吻合。

4 结论与讨论

根据气泡雾化理论，确定了气液比对豆胶气泡雾化影响的数值模拟方法及条件，分析了流场分布图及其显示的数据对豆胶雾化效果的影响，为下一步数值模拟做准备。

采用计算流体力学方法，对不同气液比豆胶与空气在喷嘴内部的流动情况进行了数值模拟，得到它们的压力场分布图、速度场分布图、组分体积分数场分布图。模拟分析结果表明:在该种模拟条件下，气液比为0.04及0.06时，相对应的豆胶与空气在喷嘴内部的流场分布图较好;雾化总能量，随气液比的增大而降低，气耗量，随气液比的增大而升高。当气液比为0.04时，流动情况较好，雾化总能量高，气耗量低，最佳气液比为0.04。以混合模拟得到的出口数据为条件，进行了仿真验证，得到了雾化颗粒粒径分布图;分析仿真验证结果得出，气液比为0.04时，雾炬锥角最大为35°，雾化颗粒直径最小为29 μm，与混合模拟得到的理论最佳气液比值相吻合。

［1］ Hamarneh A I，Heeres H J，Broekhuis A A，et al.Use of soy proteins in polyketone-based wood adhesives［J］.International Journal of Adhesion and Adhesives，2010，30(7):626 －635.

［2］ Li K，Geng X，Simonsen J，et al.Novel wood adhesives from condensed tannins and polyethylenimine［J］.In ternational Journal of Adhesion and Adhesives，2004，24(4):327 －333.

［3］ John F Schmitz.Comparison of soy-flour hydrolysates for wood adhesive systems［D］.Iowa:Iowa State University，2006.

［4］ 林巧佳，童玲，林金春.大豆基木材胶黏剂改性研究的进展［J］.亚热带农业研究，2007，3(4):284 －289.

［5］ 文博.“大豆基无醛木材工业用胶黏剂”通过新产品鉴定［J］.中国人造板，2011(9):40.

［6］ 张亚慧，于文吉.大豆蛋白胶黏剂在木材工业中的研究与应用［J］.高分子材料科学与工程，2008，24(5):20 －23，27.

［7］ 张亚慧.改性大豆蛋白胶黏剂的合成与应用技术研究［D］.北京:中国林业科学研究院，2010.

［8］ 战强，曾爱军，何雄奎，等.气泡雾化喷嘴的试验研究［J］.农机化研究，2008(2):133 －135.

［9］ 张文程，花军，贾娜，等.豆基蛋白胶气泡雾化机理的数值模拟［J］.东北林业大学学报，2013，41(2):107 －111.

［10］ 侯凌云，侯晓春.喷嘴技术手册［M］.北京:中国石化出版社，2007.

［11］ 于茂军，仇性启.气泡雾化喷嘴技术［J］.工业加热，2006，39(4):38－41.

［12］ 梁晓燕.气泡雾化喷嘴的试验研究及数值模拟［D］.南京:东南大学，2005.