基于蒙特卡罗方法的燃耗计算误差研究
2014-08-08强胜龙柴晓明
强胜龙,秦 冬,柴晓明,姚 栋
(中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610041)
用蒙特卡罗方法进行输运计算具有非常高的精度,但在耦合燃耗计算功能后,其计算的燃耗精度差强人意,特别是随着燃耗的加深,误差逐渐增大[1]。燃耗计算误差影响核设计的精度,进而影响整个堆芯的设计裕量。因此,在发展计算程序时,有必要对基于蒙特卡罗方法的燃耗(简称蒙卡燃耗)计算的误差进行深入分析。
蒙卡燃耗计算自20世纪80年代发展至今,误差研究逐渐深入。Takeda等[2]提出燃耗矩阵法,指出蒙卡燃耗误差的3个主要来源(截面、核密度、统计)并逐项分析,但该方法的数学推导较复杂,难以在程序中实现。Tohjoh等[3]提出了误差的传递效应,并给出估计误差传递的公式,但未提出如何修正误差。Dumonteil等[4]研究了蒙卡燃耗误差中统计误差的传递效应,并针对蒙卡燃耗计算过程中随机过程导致的偏差进行了分析,选择无偏差最小方差(UMV)算子用于求解波尔兹曼/贝曼方程。然而,Dumonteil等仅采用简单的数学抽样模型对UMV修正进行模拟研究,并未在实际的蒙卡燃耗程序中进行研究或应用。
本工作参考Dumonteil等的工作,对蒙卡燃耗所独有的误差进行研究,同时还针对具体的蒙卡燃耗计算程序提出相应的修正措施。
1 蒙卡燃耗误差修正研究
1.1 蒙卡燃耗误差分类
蒙卡燃耗误差的来源主要有3个:统计误差、截面误差和核密度误差。这3类误差相互影响,并随燃耗计算而传递。从误差的形成机制来看,蒙卡燃耗计算程序的误差主要有3个层次:1) 方法层次,蒙特卡罗方法导致的统计误差及其传递偏差;2) 数据库层次,中子连续能谱点截面库中裂变产额数据、单群截面数据等的误差;3) 程序层次,燃耗链方程求解及输运燃耗方程求解的误差。
其中,数据库和方程求解的误差不是蒙卡燃耗所独有,确定论方法同样存在该类问题。目前针对这两类误差的研究很多[5-7]。而统计误差则是蒙特卡罗方法所独有,特别是其传递效果。
1.2 UMV修正
若消除蒙卡燃耗计算过程中正态均值(通量φ)的非线性函数(核素含量NB(t))的偏差,可进行UMV修正,重点是对UMV修正系数进行计算。
本工作以MOI程序为基础进行研究。MOI是基于连续能量蒙特卡罗方法开发的堆芯调棒临界燃耗计算程序,在UNIX或LINUX平台下并行执行,可实现调棒临界燃耗计算。MOI计算的基本流程示于图1。
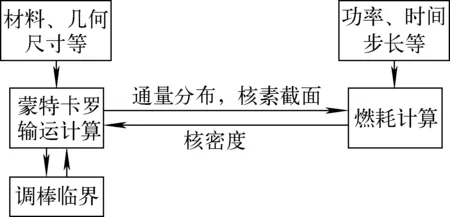
图1 MOI计算的基本流程
UMV修正系数包含σ、Ι、σ、Z、t,分别为转移截面(包括中子吸收和散射)矩阵、中子的模拟代数、中子通量的标准方差、满足(0,1)正态分布的随机向量和燃耗步长。具体计算步骤如下:
1) 从MOI的燃耗计算输入文件中获得时间步长t。
2) 从MOI输运计算输入中读取中子模拟代数I,通过蒙特卡罗模拟得到向量Z。
4) 在MOI燃耗计算输出中读取矩阵σ,求出UMV修正系数矩阵cos(σξt)。其中:
Z由正态分布中抽样得到,正态分布示于图2。
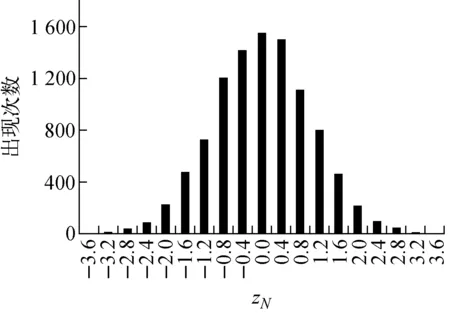
图2 正态分布示意图
5) MOI燃耗计算输出的核素含量乘以修正系数(矩阵),即可得到修正后的核素含量NNB(t):
NNB(t)=NB(t)cos(σξt)
UMV修正流程示于图3。
以一体式可燃毒物(IFBA)单栅元例题为例(图4,UO2芯块富集度为3.2%),采用UMV修正后238U的相对修正量((修正后质量-修正前质量)/修正前质量)随燃耗的变化示于图5,达到了Tohjoh等[3]观察到的10-5量级。这说明UMV修正可改善核素含量。
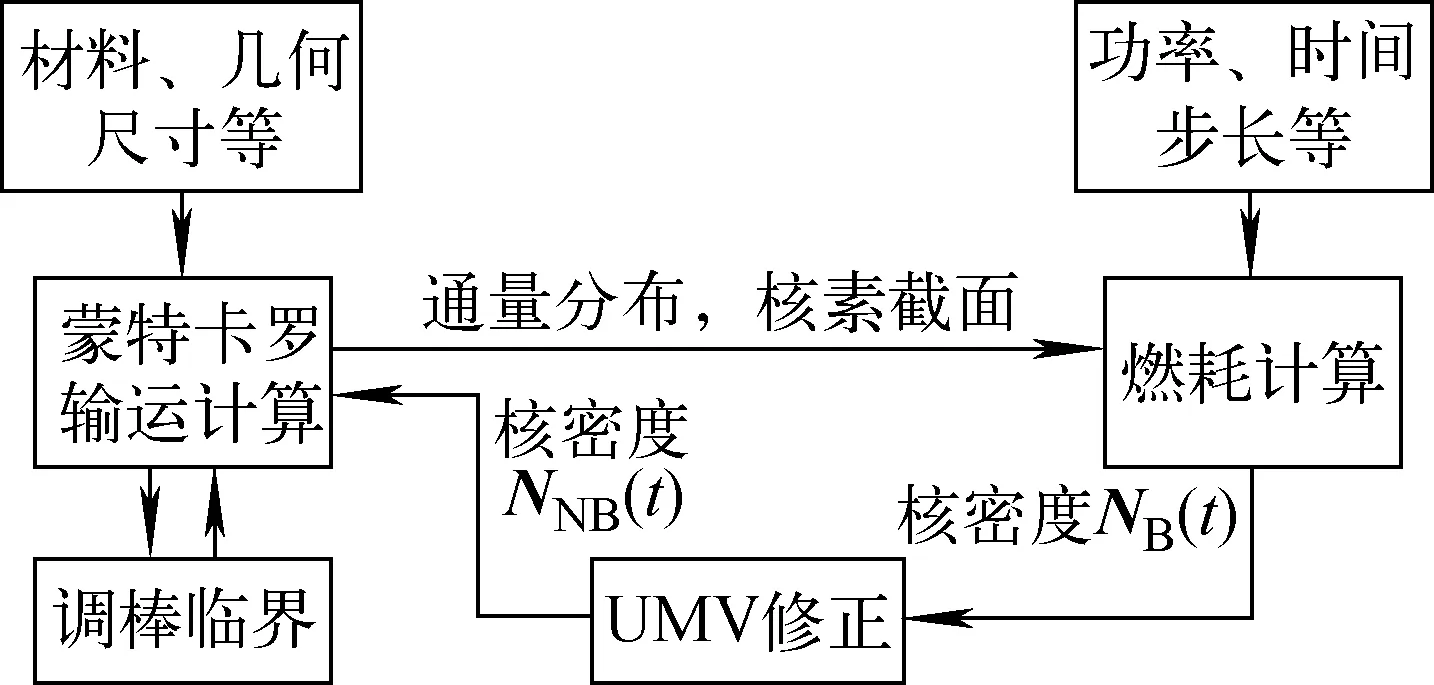
图3 UMV修正流程
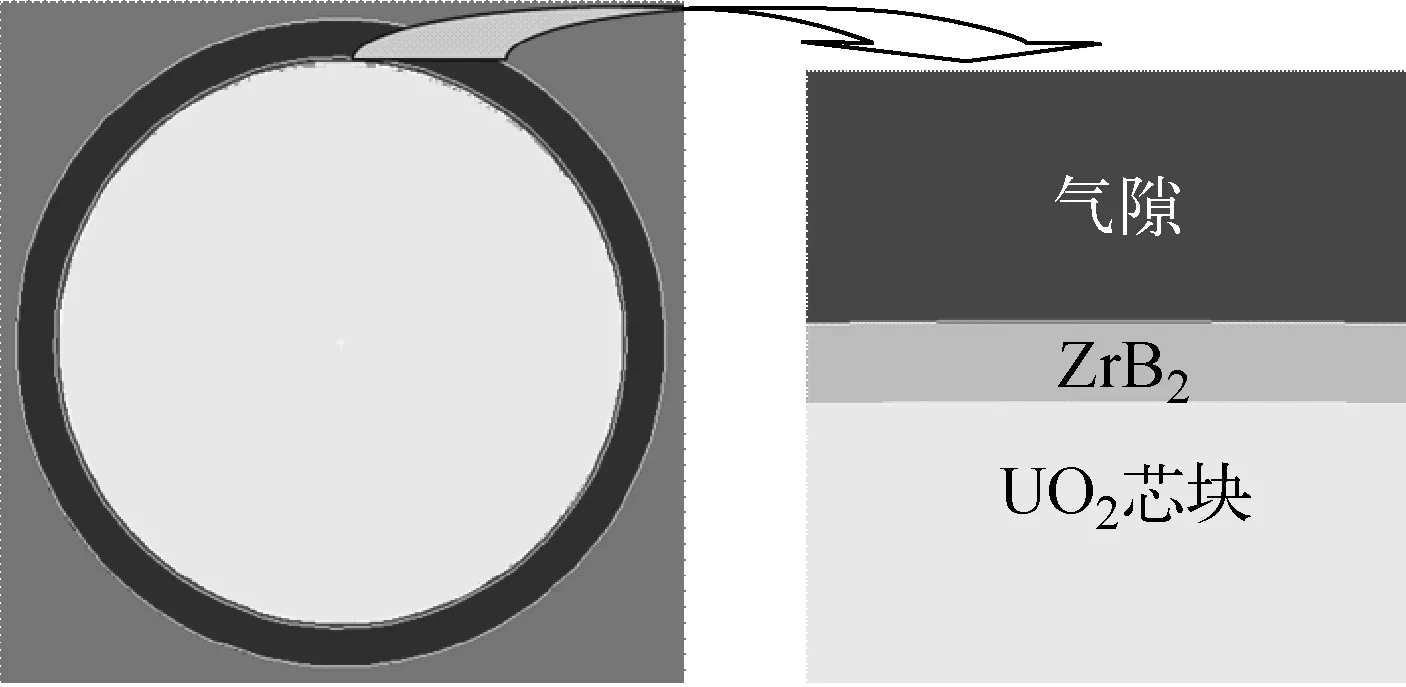
图4 IFBA栅元示意图
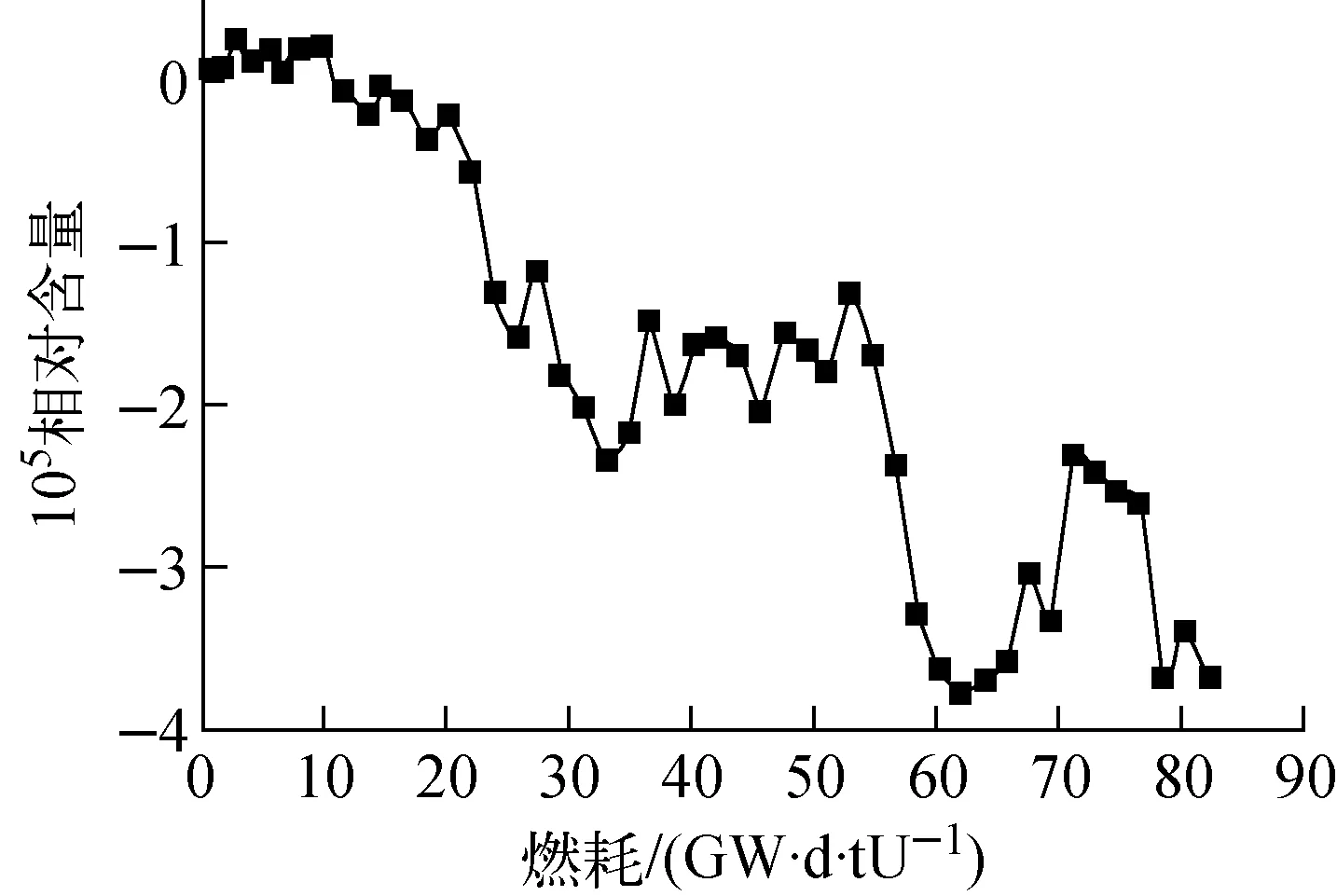
图5 238U修正量随燃耗的变化
但UMV修正对kinf的影响甚微。仍以IFBA单栅元例题为例,与西屋公司开发的Paragon程序进行对比验证,同时还给出了阿海珐公司APOLLO2-F程序的计算结果(图6)。Paragon与APOLLO2-F均广泛应用于商用核电厂的设计和后续技术服务,大量的运行和实验数据反馈保证了程序的准确性,因此选择这两个程序作为参考。计算结果显示,采用UMV修正后的kinf仍存在较大误差。
1.3 密度修正
蒙卡燃耗计算程序除统计误差及其传递效应外,其燃耗核素的选择也会影响程序的精度。不同程序采取的策略不同:如MCODE[8]采取固定的核素选取;MCBurn[9]采用核素筛选三原则(优先考虑吸收率,其次质量分数,以及重要核素等);RMC[10]采用按宏观吸收率份额筛选。
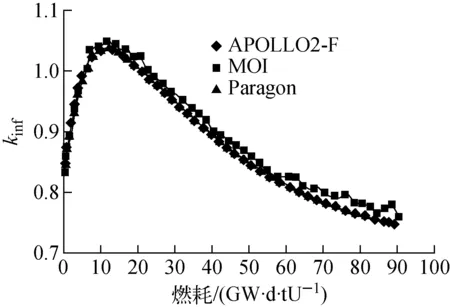
图6 kinf随燃耗的变化
无论采用何种策略,燃耗核素越多,则燃耗计算精度越高,但相应的计算效率越低。以MCODE为例,在计算某单栅元例题时,为了高精度,选择了39种锕系核素和100种裂变产物,保证了99.95%的质量和中子吸收份额[8]。然而,该燃耗计算耗时4 d(DEC alpha工作站,每次MCNP计算耗时1 h),在处理较大规模的问题时,该筛选策略会导致计算时间无法接受。
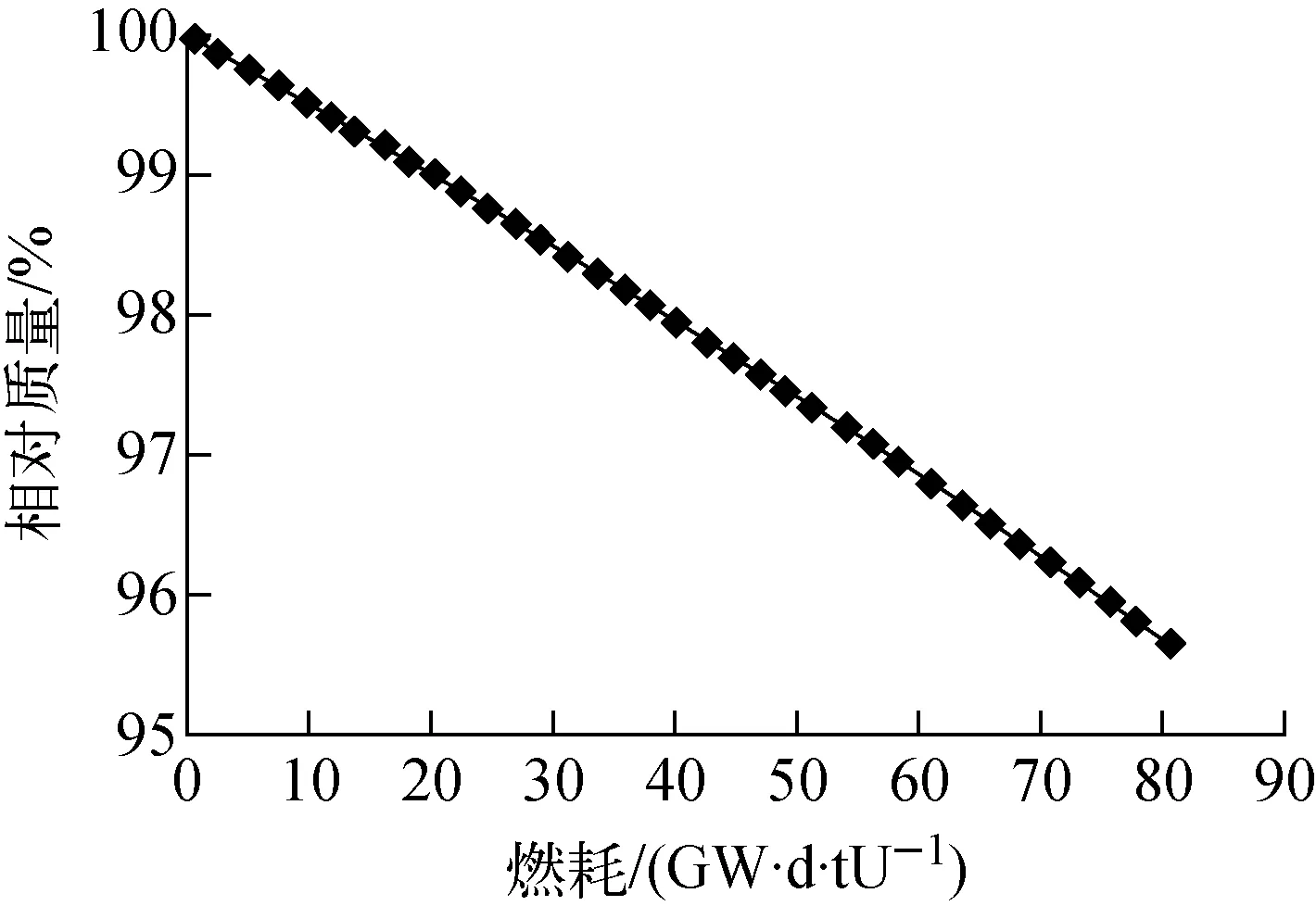
图7 燃料芯块相对质量随燃耗的变化
MCBurn等程序优先考虑以吸收率份额筛选,在一定程度上减少了不必要的核素计算。然而,该筛选策略可能导致不参与输运计算的裂变产物逐渐增多,因此筛选后的燃料质量随燃耗的增加而降低(图7,按99.99%吸收率份额进行筛选)。蒙特卡罗输运计算通常输入核素的相对含量,一旦总质量发生变化,必须改变相应燃料区的密度,才能真实反应核素的质量。
MOI采用按吸收率份额筛选的原则(同时也考虑重要核素如241Am、243Am等,该类核素随燃耗逐渐积累,在深燃耗下作用较大),因此随燃耗的变化,MOI按照各燃耗区核素质量的不断变化修正各燃耗区的密度(简称密度修正),从而保证各燃耗步下蒙特卡罗输运计算的准确性。
密度修正的公式为:
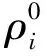
通过修正各燃耗区的密度,可避免密度误差导致核素质量的输入误差,保证蒙特卡罗输运计算的准确性。
1.4 误差修正效果
通过对蒙卡燃耗统计误差传递效应的研究,提出了改善核密度的UMV修正;同时针对核素筛选导致的质量变化,提出了保证蒙特卡罗输运计算精度的密度修正。
除UMV修正和密度修正外,选择合适的截面库也很重要,包括输运计算的连续截面库和燃耗计算中采用的燃耗截面库。在MOI研制过程中,对截面库也进行过一些改进,如通过修正燃耗截面库中Nd的裂变产额,改善143Nd的核密度。
图8示出IFBA例题误差修正后的计算结果。
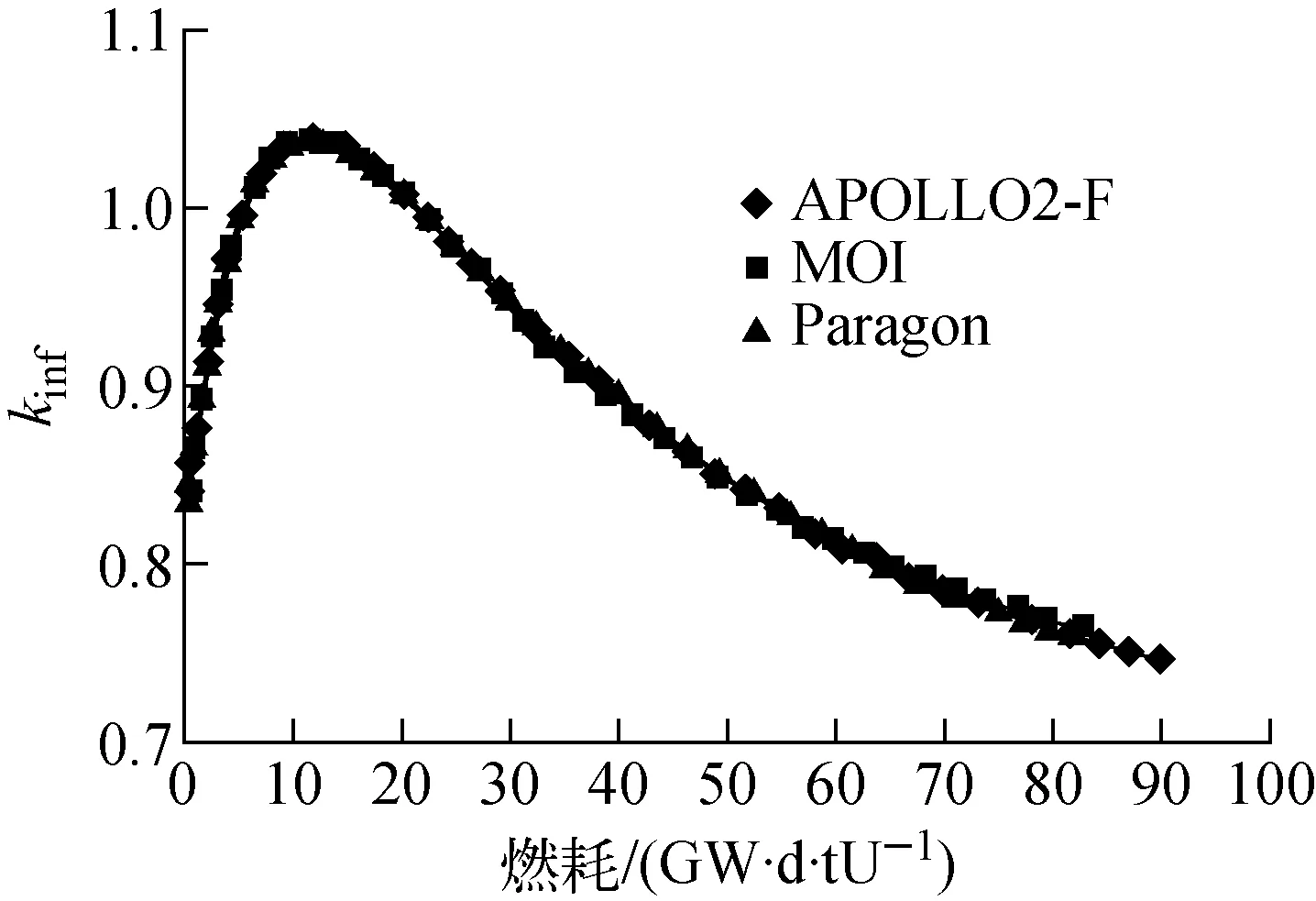
图8 误差修正后kinf随燃耗的变化
2 程序验证
验证基准题[11]采用的栅元模型来自西屋压水堆17×17组件,如图9所示。采用ThO2-UO2芯块来替代UO2燃料芯块,实际密度是理论密度的94%;重核素中Th的质量占75%,U的质量占25%(235U的富集度为19.5%)。表1、2列出西屋压水堆组件单栅元模型的详细参数,本工作的基准计算采用热态满功率参数。
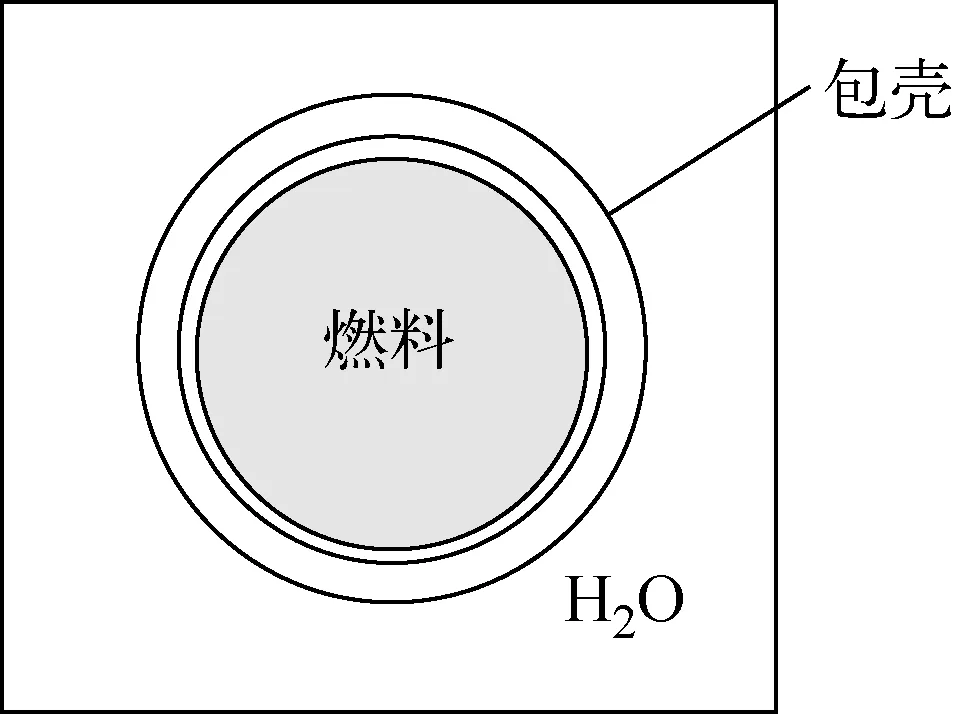
图9 单栅元模型
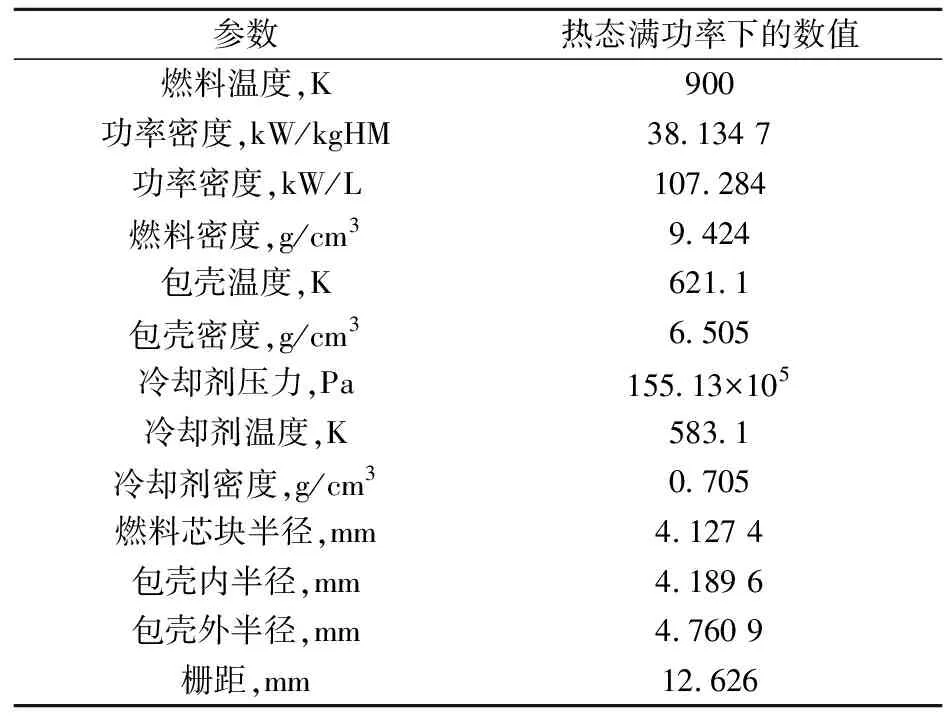
表1 单栅元模型参数
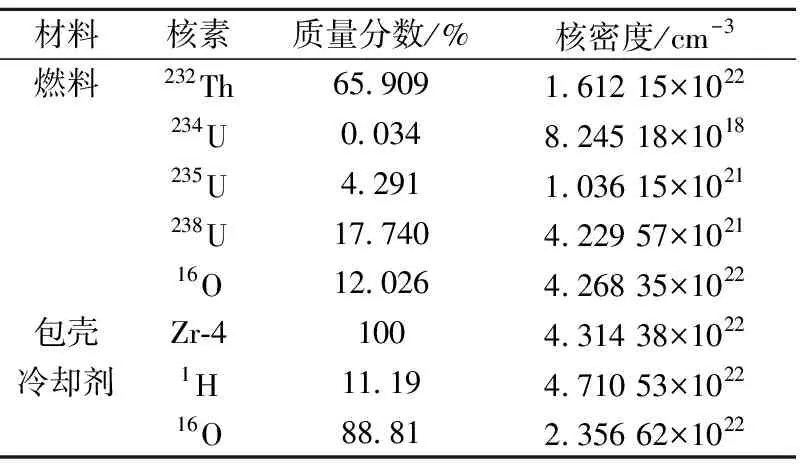
表2 热态满功率下栅元的初始成分
采用基准题计算的棒栅元kinf随燃耗的变化示于图10。作为比较,图10中同时给出CASMO-4、MIT和INEEL采用MOCUP的计算结果。由图10可见,MOI计算的kinf与MIT-MOCUP的结果几乎完全一致。不同程序计算的棒栅元各核素含量与CASMO-4的相对误差示于图11。由图11可见,MOI计算的核密度与CASMO-4的相对误差均在7%以内,而MOCUP计算的个别核密度与CASMO-4的相对误差超过10%。
由图10、11可知,误差修正后,MOI的计算精度得到了改进,单栅元模型计算的有效增殖因数达到了国际同类程序的水平,而核密度则更接近成熟的商业程序CASMO-4,为MOI的实际应用奠定了基础。
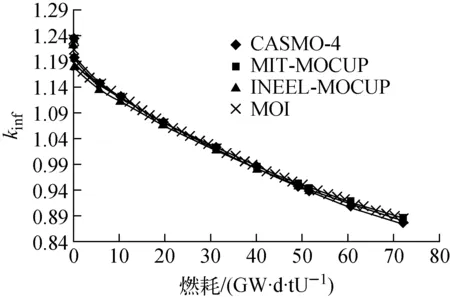
图10 基准题棒栅元kinf随燃耗的变化
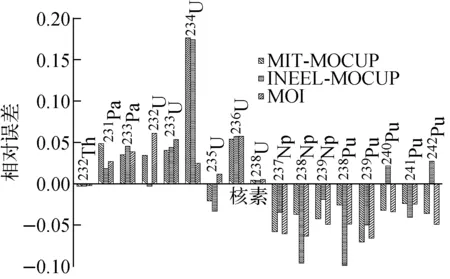
图11 不同程序计算的棒栅元各核素含量与CASMO-4计算结果的相对误差
3 结论
本工作对影响蒙卡燃耗计算误差的原因进行了分类,对蒙特卡罗方法统计误差的传递效应进行了研究。以MOI为基础,采用UMV修正、密度修正等措施,在一定程度上降低了蒙卡燃耗计算中的误差,有利于蒙卡燃耗计算程序在反应堆工程设计验证中的应用。
参考文献:
[1] BAKKARI B E, ELBARDOUNI T, NACIR B, et al. Accuracy assessment of a new Monte Carlo based burnup computer code[J]. Annals of Nuclear Energy, 2012, 45: 29-36.
[2] TAKEDA T, HIROKAWA N, NODA T. Estimation of error propagation in Monte-Carlo burnup calculations[J]. J Nucl Sci Tech, 1999, 36: 738-745.
[3] TOHJOH M, ENDO T, WATANABE M, et al. Effect of error propagation of nuclide number densities on Monte Carlo burn-up calculations[J]. Annals of Nuclear Energy, 2006, 33: 1 424-1 436.
[4] DUMONTEIL E, DIOP C M. Biases and statistical errors in Monte Carlo burnup calculations: An unbiased stochastic scheme to solve Boltzmann/Bateman coupled equations[J]. Nuclear Science and Engineering, 2011, 167: 165-170.
[5] YAMAMOTO A, TATSUMI M, SUGIMURA N. Numerical solution of stiff burnup equation with short half lived nuclides by the Krylov subspace method[J]. Journal of Nuclear Science and Technology, 2007, 44(2): 147-154.
[6] ISOTALO A E, AARNIO P A. Substep methods for burnup calculations with Bateman solutions[J]. Annals of Nuclear Energy, 2011, 38: 2 509-2 514.
[7] ISOTALO A E, AARNIO P A. Higher order methods for burnup calculations with Bateman solutions[J]. Annals of Nuclear Energy, 2011, 38: 1 987-1 995.
[8] XU Zhiwen, HEJZLAR P, DRISCOLL M J, et al. An improved MCNP-Origen depletion program (MCODE) and its verification for high-burnup applications[C]∥PHYSOR 2002. Seoul: [s. n.], 2002.
[9] 余纲林,王侃. MCNP和ORIGEN2 耦合系统(MCBurn)的研究[D]. 北京:清华大学,2002.
[10] 佘顶,王侃,余纲林. 堆用蒙卡程序燃耗计算功能开发[J]. 核动力工程,2012,33(3):1-5.
SHE Ding, WANG Kan, YU Ganglin. Development of burnup calculation function in reactor Monte Carlo code RMC[J]. Nuclear Power Engineering, 2012, 33(3): 1-5(in Chinese).
[11] WEAVER K D, ZHAO X, PILAT E E, et al. A PWR thorium pin cell burnup benchmark[C]∥PHYSOR 2002. Seoul: [s. n.], 2002.
