基于改进四叉树模型的统计静态时序分析

潘 旻，喻明艳

（哈尔滨工业大学国际微电子中心，威海264209）

·大规模集成电路设计、制造与应用·

基于改进四叉树模型的统计静态时序分析

潘 旻，喻明艳

（哈尔滨工业大学国际微电子中心，威海264209）

提出一种改进的静态时序分析方法，该方法通过对片内工艺变化参数随机变量进行改进四叉树模型分解，然后建立多层分布空间关系指数函数方程组求得片内相邻、次邻块间影响的拟合权重系数，使得非独立的随机变量转化为一系列相互独立的随机变量线性相加的形式，最后遍历获取表征片内工艺参数变化空间关系的协方差矩阵。通过和Monte-Carlo方法以及Minnssta方法仿真结果对比，验证了改进方法的精确性，同时也表明了该方法在降低片内非独立空间关系复杂性方面的有效性。

工艺参数变化；空间关系；统计；四叉树；静态时序分析

1 引 言

随着超大规模集成电路制造工艺逐步迈入深亚微米时代，芯片上互连线以及器件的尺寸和间隔迅速缩小，片上系统的信号频率也急剧增加［1］。这些趋势给互连线的寄生电阻和寄生电容带来了不可忽视的影响，并随之引发决定系统性能和可靠性的相关问题，比如电路串扰和电路延时。电路延时信息是静态时序分析中时序验证的基础，由电磁波传输延时和上升沿延时组成，它决定了电路时钟频率的上限。实际上，由于芯片制造工艺的局限性，片内工艺参数并不是常数，然而即使存在很微小的变化都会带来电路延时的巨大变化，所以在静态时序分析中考虑工艺参数变化是必不可少的。近些年来很多学者和研究人员致力于这一领域，并有了一定的研究成果［2-4］。

现如今，有很多不同的并且行之有效的仿真方法来对带随机变量的集成电路问题进行时序分析。传统上，人们会采用计算机仿真软件例如PSpice，MentorGraphics，Cadence，Viewlogic，MicroSim等来进行Monte-Carlo统计分析［5］。虽然Monte-Carlo方法能够逼真的描述随机对象的特性和实验过程，但它的收敛速度和一些数值方法相比比较慢，并且它的误差大小是不确定的。为了克服这些缺点，采用基于改进四叉树多层分布空间关系模型的新方法，该方法能够很好的处理片内工艺参数非独立随机变量，充分考虑了片内相邻、次邻块间工艺参数的空间关系，求得统计静态时序分析中所需的协方差矩阵。和Monte-Carlo方法相比，它只需耗费很少的时间就能达到与其差不多的精确度。

2 片内和片间工艺参数变化分析

工艺参数变化通常分为片间变化和片内变化这两种成分，其中片内变化可以进一步分解为随机变量和空间相关变量。因为这里考虑了片内变化的空间关系，所以这些随机变量并不是相互独立的，它们之间的关系可以用协方差矩阵的形式来表示，在这样的空间关系架构下，布局越近，门与门之间的空间关系越强，反之亦然。这种片内工艺参数间的空间关系可用简单的由如图1所示的平面模型来建模。从图1可以看出，在随机变量服从正态分布的情况下，参照点O和距离其最远点（W，H）处的工艺参数变化差值达到了最大的3σ，呈现的空间相关关系也就最小。同样，当把晶片划分为块状模型来建模时，靠的越近的块空间关系越强，相反，靠的越远的块之间空间关系就越小。很多空间关系模型，例如文献［6］在建模块与块之间的空间关系时，只考虑了相邻块间的空间关系，而忽略了次邻块间，即对角块间的空间关系，这就会带来很大的误差。

图1 片内工艺参数变化平面模型图

为了求得片内工艺参数变化的空间关系，首先需要对片内和片间的工艺参数变量进行建模。传统上，一个特定晶片上任意门k的工艺参数变化量Ptotal，k是名义上的工艺参数值Pnom，片间的门工艺参数变化量△Pinter和片内的门工艺参数变化量△Pintra，k三者的代数和［3］：

其中，Pnom代表所有晶片的工艺参数变化均值，△Pinter和△Pintra，k都是随机变量，在建模时，可以假设△Pinter和△Pintra，k都服从截尾的正态分布，当然其他任何合适的分布都可以采用。那么根据这个工艺参数变化量的模型，任意门k的延时dk可以表示为：

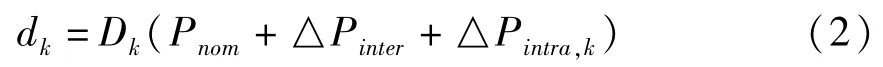
式中的函数Dk一般情况下是非线性方程，这就比较难处理，但是片内工艺参数随机变化量△Pinter和△Pintra，k通常都很小，3σ值小于Pnom的15%。因此，门延时的变化和工艺参数的变化可视为线性关系，从而式（2）就可以处理成如下形式：

式（4）采用了一个简单的线性近似，这样的近似对目前的工艺参数变化来说有很好的精确度［7］。由于这里并没有考虑片内工艺参数变化随机变量间的空间关系，所以dk是一系列相互独立的随机变量和的形式，这就非常方便后续处理。而一旦引入空间关系，为了降低分析的难度，就要将非独立的变量△Pintra，k进行分解，进而转化为独立的随机变量，这就需要求取表征块间空间关系的协方差矩阵。

3 考虑空间关系的改进四叉树分层模型

为了将空间关系有效的考虑进来，首先将晶片的面积分割为四叉树多层次分布［8］，对于每个层次i（i＝0，1，2，...，n），晶片面积被划分成2i×2i个方格。图2显示的就是一个晶片通过3层分割的例子，其中最顶层（第0层）只有一个区域，并且这个区域范围覆盖了整个晶片，被以下所有的层次共享，最底层（第n层）拥有4n个区域。分配给每个特定层次下所有的随机变量相同的概率分布以及将整个片内变量分给这些不同的层次，这样每层的每个区域（i，j）和一个独立的正态随机变量联系起来，以此来表示总共片内工艺参数变化量的一部分成分，那么片内门k的工艺参数变化就可以定义为所有与之相关的随机变量△Pi，j代数和的形式：

其中△Pi，j是和四叉树相关的服从正态分布的随机变量，△Prandom，k是每个门k和空间关系无关的独立随机变量，层次i的变化范围是从0到n，任何特定层次下的区域j指的是其投影能够覆盖到门k位置的那个区域。

这里定义在四叉树中每个节点的任意一个子树根据相对位置关系，和其余三个子树存在且仅有两种空间关系，即相邻关系和对角关系，那么就可以将每个层次任意网格中的变量对所投影的子层次网格变量的空间影响进行建模。

图2 四叉树多层次分布模型图

现在以第二层，即图2中的第1层和区域（1，1）相关的区域为研究对象，那么区域（1，1），（1，2），（1，3），（1，4）的片内门工艺参数变化量就可以表示如下：

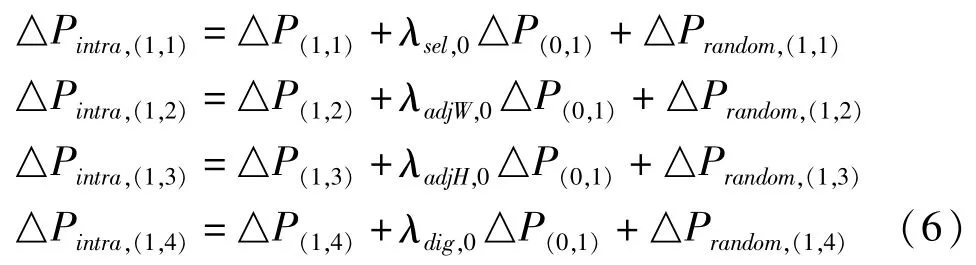
将上四式改写为用矩阵表示的紧凑形式：

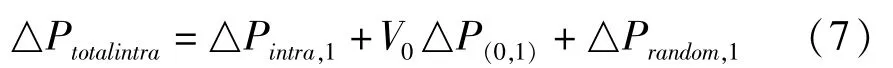
其中

因为第i层每个网格区域的边长为W／2i，所以就有dsel＝0，dadjW＝W／2i，dadjH＝H／2i，ddig＝（W2＋H2）1／2／2i。然后这里假定模型的空间关系影响函数为指数函数形式［9］，则第i＝1层的关于0层变量的分布关系拟合权重系数方程组为：

求解式（12）方程组，就能得到顶层的拟合权重系数矩阵V0的值。图3所示的是将整个晶片细化成3层后的四叉树网格投影图，通过这样不断对生成的网格进行进一步细化，反复求解分布关系拟合权重系数方程组，第i层的空间关系影响拟合权重系数矩阵Vi就能依次被求出。

4 遍历求取空间关系协方差矩阵

当空间关系模型确立后，只要选取合适的层数，底层每个区域的随机变量组成成分就可以确定，片内工艺参数变化就可以表示为如下形式：

图3 3层四叉树网格投影图

其中任何特定层次下的区域j指的是和具体门的位置相交的那个区域，i的变化范围从0到n-1。这样底层每个网格的工艺参数变化都可以用一系列独立的随机变量成分线性相加的形式表示，所有网格的片内变化可以由2n×2n的矩阵X表征：

通过遍历矩阵X中每个元素就可以求得每个网格的方差以及和其处于相邻关系以及斜对角关系网格的协方差：

在改进模型中，某些布置在同个网格中的门要比虽然布置在很靠近的位置，但是落在不同网格中的门的相关关系来的强，例如图3所示，门B和门A之间的空间关系要强于门B和门C之间的空间关系，虽然门B与门C布置的非常近。因此，对四叉树空间关系模型层次分的越细，最底层相同区域、相邻区域以及对角区域内的门与门之间越能保持工艺参数变化的一致性，虽然这样能更准确地模拟真实情况，但不可避免的是建模复杂度也就越高，仿真越耗时，因此为了适当地对片内工艺参数进行建模，就需要在准确度和复杂度之间做一个折衷。

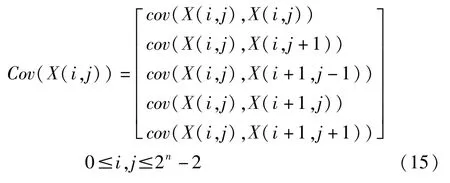
5 改进的四叉树模型方法仿真分析

实验模拟在Linux下完成，Linux内核版本为Linux 2.6.9，操作系统为Red Hat Enterprise Linux AS release 4（Nahant Update 8）。实验硬件配置为Intel（R）Xeon（R）型号的CPU，主频为2.4GH，内存为12G。仿真分析的benchmark电路是s38417，这里考虑以下这些晶体管的工艺参数［10］：栅长Lg，栅宽Wg，线宽Wi，线厚Ti，ILD厚度HILD。

图4和图5分别是电路延时的累积分布密度曲线和概率密度函数曲线仿真结果。改进方法的延时均值误差为-0.0753%，延时标准差误差为-0.0592%，从图中也可以看出较Minnssta方法而言，改进方法和Monte-Carlo方法仿真结果更为接近，这也说明改进方法是行之有效的。

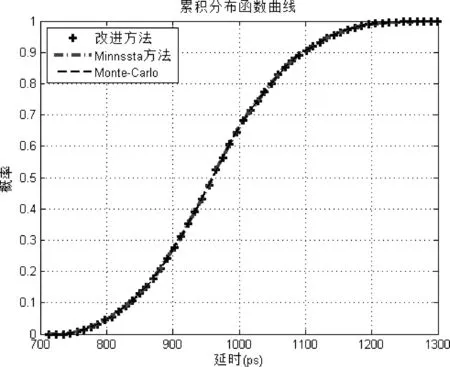
图4 仿真电路延时的累积分布函数曲线

6 结束语

针对片内工艺参数的非独立随机变化，提出了改进的基于四叉树多层分布空间的关系模型方法，考虑了处于相邻位置和次邻位置网格间的空间影响关系，求解出了线性拟合权重系数，并进一步得到包含片内不同位置空间关系的协方差矩阵。通过实验仿真，验证了该方法的精确性和有效性，为解决统计静态时序分析中其他种类的含非独立随机变量的独立主成分分解问题提供了新的思路。

图5 仿真电路延时的概率密度函数曲线

［1］JCong，Z Pan，L He，et al.Interconnect Design for Deep Submicron IC’s［J］.IEEE／ACM International Conference on Computer-Aided Design，1997：478-485.

［2］H Chang，S S Sapatnekar.Statistical Timing Analysis Under Spatial Correlations［J］.IEEE Trans.on Computer-Aided Design of Integrated Circuits and Systems，2005，24（9）：1467-1482.

［3］A Agarwal，D Blaauw，V Zolotov，et al.Statistical Delay Computation Considering Spatial Correlations［J］.IEEE／ACM Asia-Pacific Design Automation Conf，2003：271-276.

［4］B Stine，D Boning，JChung.Analysis and Decomposition of Spatial Variation in Integrated Circuit Processes and Devices［J］.IEEE Trans.on Semicond.Manuf，1997，10（1）：24-41.

［5］D Frenkel.Introduction to Monte Carlo Methods［J］.NIC Series，2004（23）：29-60.

［6］H Chang，SSSapatnekar.Statistical Timing Analysis Considering Spatial Correlations Using a Single PERT-like Traversal［J］.IEEE／ACM International Conference on Computer-Aided Design，2003：621-625.

［7］A Gattiker，SNassif，R Dinakar，et al.Timing Yield Estimation from Static Timing Analysis［J］.Quality Electronic Design，2001：437-442.

［8］A Agarwal，D Blaauw，V Zolotov.Statistical Timing Analysis for Intra-Die Process Variations with Spatial Correlations［J］.IEEE／ACM International Conference on Computer-Aided Design，2003：900-907.

［9］R Shen，SX.-D.Tan，JXiong.A Linear Algorithm for Full-Chip Statistical Leakage Power Analysis Considering Weak Spatial Correlation［J］.IEEE／ACM International Great Lakes Symposium on VLSI，2010：227-232.

［10］SNassif.Delay variability：Sources，impact and trends［J］.IEEE International Solid-State Circuits Conference，2000：368-369.

Statistical Static Tim ing Analysis Based on Modified Quad-Tree Model

PAN Min，YU Ming-yan
（International Microelectronics Center，Harbin Institute of Technology，Weihai264209，China）

In this paper，amodified approach for static timing analysis is presented.It decomposes intra-die random variables based on modified quad-tree distribution model and makes the dependent random variables as a linear sum of independent random variables，by solving themulti-level distributed spatial correlation equations，which are related to exponential functions，to obtain the fittingweight coefficients of adjacentand diagonal intra-die squares.Consequently，the covariancematrix，which represents for the spatial correlations of intra-die process variations，can be derived through traversal.The simulation results，from Monte-Carlomethod and Minnsstamethod，confirm the accuracy ofmodified approach and show that it is effective in reducing the complexity of analyzing the dependent spatial correlations.

Process Variation；Spatial Correlation；Statistical；Quad-Tree；STA

10.3969／j.issn.1002-2279.2014.05.001

TN402

：A

：1002-2279（2014）05-0001-04

潘旻（1989-），男，江苏南通人，硕士研究生，主研方向：电子电路系统建模与数值仿真，数字集成电路设计。

2014-02-12