失配电流控制的高阶带隙基准工艺健壮性研究
2014-08-07朱光荣聂卫东于宗光
朱光荣,尹 岱,聂卫东,,于宗光
(1.无锡友达电子有限公司,无锡214028;2.江南大学电子工程系,无锡214122)
·大规模集成电路设计、制造与应用·
失配电流控制的高阶带隙基准工艺健壮性研究
朱光荣1,尹 岱1,聂卫东1,2,于宗光2
(1.无锡友达电子有限公司,无锡214028;2.江南大学电子工程系,无锡214122)
分析了基于失配电流控制的高阶补偿带隙基准的补偿原理,并研究了工艺偏移对基准电压温度系数的影响。基于失配电流控制的补偿策略具有结构简单、控制精度高,而且可以通过调整失配电流和多晶电阻阻值,使带隙基准具有较低的温度系数,同时具有较强的工艺健壮性。模拟分析表明,在-25℃-125℃温度范围内,在TT(Typical-Typical)工艺角下,带隙基准的温度系数为4.8ppm/℃,同时在其他工艺角下,带隙基准的温度系数都可控制在9.0ppm/℃以下。通过无锡上华科技(CSMC)0.18μm CMOS工艺实验验证,采用这种简单失配电流控制的高阶补偿带隙基准,在3V电源电压下,在-20℃-120℃温度范围内,带隙基准的温度系数最低为6.9ppm/℃。
带隙基准;高阶补偿;温度系数;工艺健壮性
1 引 言
一阶线性电压补偿是产生带隙基准的基本方法,可通过电压模或电流模的一阶线性补偿策略来获得温度系数(Temperature Coefficient,TC)为20-100ppm/℃左右的带隙基准[1-2]。进一步降低基准电压温度系数需要采用高阶补偿策略,可采用指数曲率温度补偿法[3],线性化补偿法[4],分段补偿法[5-6],双电流补偿法[7],还可利用不同材料的相异温度特性进行高阶补偿等[8],都能将温度系数控制在5ppm/℃以下。以上各类传统的高阶补偿结构均依赖于附加的电路结构,而且基准电压随工艺波动会发生显著变化,工艺参数的漂移将导致基准电压温度系数的严重退化,甚至产生10倍左右的恶化。最差状态下,高阶补偿的温度系数甚至比一阶线性补偿的更差,从而严重限制了高阶补偿的实用价值。
首先分析了利用电路内部的非线性失配电流实现高阶补偿的方法[9-11],接着讨论了电流模带隙电压基准温度系数的工艺健壮性。通过调整可控的失配电流和多晶电阻阻值,使得在不同工艺偏移情况下,一阶补偿与高阶补偿能相互抵消,从而保证在不同的工艺角下,带隙基准的温度系数都能控制在较小的范围。模拟分析表明,在-25℃-125℃范围内,所设计的电流模高阶补偿的带隙电压基准,其输出电压的温度系数TC在TT(Typical-Typical),SS(Slow-Slow),FS(Fast-Slow),SF(Slow-Fast),FF(Fast-Fast)等工艺角下,都小于9.0ppm/℃。通过无锡上华科技(CSMC)0.18μm CMOS工艺实验验证,-20℃-120℃温度范围内,采用这种简单的失配电流控制的高阶补偿带隙基准的温度系数,测试最小值为6.9ppm/℃。

图1 基于失配电流ΔI控制的电流模高阶补偿带隙基准
2 基于失配电流控制的高阶补偿带隙基准[9-11]
图1为所采用的基于三路耦合闭环反馈偏置的电流模补偿基准电路。在偏置电流I0,I1和I2完全匹配的条件下,得到的一阶线性补偿基准输出电压Vref为:
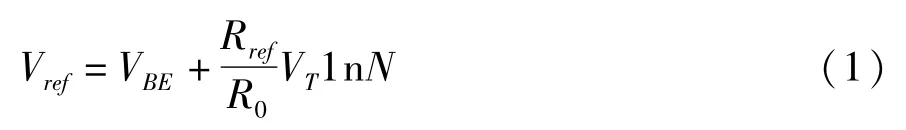
Q0与Q1两PNP管发射区面积之比为N,VBE为Q4发射极BE结的正向压降,VT为热电压。图1中,Rref=R1+R2。当考虑高阶温度系数时,PNP管Q4的BE结正向压降为[12]:

式中T0取300K,VBE(T0)为T0温度下的BE结正向压降,γ、α分别为与三极管基区空穴迁移率和集电极电流指数温度系数相关的系数。VG(T)为硅的带隙电压,其与温度有关,可表示为[12]:

VG(T0)为T0温度时的能隙电压,TC1(VG),TC2(VG)分别为VG(T)的一阶和二阶温度系数。
综合(1),(2)和(3)式,当VBE(T)的一次项被完全补偿后,可得出只剩下0次项(常数项,与温度无关)和高阶项的基准电压为

(4)式中,VG0为理想带隙基准输出(与温度无关),VA_NL为高阶补偿量,用来补偿VBE(T)和VG(T)中的高阶分量。
对于图1的基准电路,当VC0=VC1时,一阶平衡,此电路类似于常规的一阶线性补偿带隙基准电路。当控制VC0与VC1不相等时,失配电流ΔI=I1-I0,此时Q0与Q1的BE结压降差:

β=I1/I0=1+ΔI/I0。当ΔI/I0→0时,ln(1+ΔI/I0)≈ΔI/I0,VTlnβ≈VT×ΔI/I0。
因此,图1所示的基准带隙电压源的输出电压为:

此时,如图1所示,则系统通过失配控制引入的高阶补偿电压为:

显然电路提供的电压量VTln N×Rref/R0对系统进行了一阶温度补偿。而电压量VNL_A是利用电阻的一阶线性与二阶非线性温度系数,在失配电流ΔI的调制下实现高阶补偿。电路采用多晶硅电阻,考虑其温度特性,Rref=Rref0[1+TC1(T-T0)+TC2(T-T0)2]。对于CSMC 0.18μm CMOS工艺,一阶温度系数TC1为负(TC1=-0.97×10-3)、二阶温度系数TC2为正(TC2=1.85×10-6),两者分别在中低温和中高温范围内起作用。由于ΔI为与温度近似无关的常数,只需通过ΔI的正负极性控制和大小设置,同时通过多晶硅电阻的非线性温度特性,即可获得不同性质和不同温度范围的温度补偿量。所以通过设计选取适当的Rref和ΔI,式(4)中的高阶温度量VA_NL可以由补偿电压VNL_A获得补偿,从而得到更低温度系数的基准电压源。
由于利用了系统的失配控制进行高阶补偿,所以线路系统中各器件的随机失配必须进行优化设计,以减少随机失调电压与电流。除了完成启动功能的PM8,PM9可按最小规则进行设计外,其余MOS管的最小沟长为2μm,PNP管Q0,Q1,Q2和Q3的发射区面积为10μm×10μm,并对要求严格的MOS对管和PNP管进行了对称设计,交叉设计,冗余设计和共质心布局,以保证工艺随机失调及其他不需要的系统失调不会影响系统的失配控制。
3 工艺健壮性研究与设计
工艺漂移引起基准温度系数变化的根源主要来自两个方面,首先是一阶线性补偿漂移,其次是高阶补偿分量漂移。受工艺波动影响,VBE中的一阶线性负温度系数(VG(T0)-VBE(T0))/T0必然发生漂移,而其正温度补偿量VTln N×Rref/R0中的线性比例系数由电阻比决定,而电阻比在工艺漂移下仍能保持恒定,导致一阶线性正温度与VBE中一阶线性负温度的补偿发生偏离,造成温度系数的显著变化。
而且,工艺漂移带来电路结点电位与电流失配状态的变化以及多晶电阻的变化。当失配电流ΔI变化时,导致高阶补偿变化,而其多晶电阻的补偿包含一阶线性分量与二阶非线性分量。因此,若高阶补偿漂移与一阶线性补偿漂移方向相反,其作用可以相互抵消时,工艺漂移对基准温度系数的影响可大幅降低。
基于失配电流控制的高阶补偿带隙基准,为提高其工艺健壮性,还需对ΔI失配状态进行优化控制。设在TT工艺角下,实现最优高阶补偿所需的最大失配电流为ΔImax,此时,当0<ΔI<ΔImax时,基准温度特性介于理想高阶补偿与典型一阶补偿的中间状态,ΔI由于较小而达不到最佳补偿效果,因此温度系数比理想二阶补偿略大,但仍比一阶小。在此状态下,当工艺漂移时,导致一阶温度特性与高阶补偿特性均发生变化,但由于适当的ΔI调制作用,存在某一特性的ΔI状态点,既保留了较强的线性补偿与高级补偿相互抵消的特性,即高阶补偿充分有效,同时也由于线性补偿和高阶补偿随工艺漂移而相互抵消,从而抑制引起的基准输出温度特性变化,最终实现工艺健壮性控制。可以预测,存在某一状态工作点,即在0~ΔImax范围内某一特定的ΔI,尽管其基准温度特性在典型工艺条件TT状态下,不一定最佳,但可以实现基准温度特性较好的工艺健壮性。
4 仿真验证与分析
基于Spectre仿真工具及CSMC 0.18μm CMOS工艺模型,调整失配电流ΔI和多晶电阻Rref阻值,在不同工艺角下,模拟分析了带隙基准电压温度特性。
图2为基准电路在-25℃-125℃温度范围内的温度特性仿真验证波形。其中,方案1与方案2的失配电流ΔI分别为2.15nA和1.40nA,多晶电阻Rref阻值分别为47.2772kΩ和47.4074kΩ。从图2(a)可发现,在典型TT工艺角下,方案1和方案2都呈现出高阶补偿特性,其温度补偿特性为“M”形,方案1的温度系数为1.9ppm/℃,而方案2的温度系数为4.8ppm/℃。模拟结果表明在SS,FS,SF,FF工艺角下的温度系数,方案1分别为5.7,6.4,7.9和14.8 ppm/℃,方案2分别为6.3,8.7,5.6和6.7 ppm/℃。从图2(b)和(c)可见,在SF和FF工艺角下,随着温度的升高,方案1的正温度补偿特性明显强于负温度补偿特性,因此,输出电压呈现出单调的正温度系数,特别在FF工艺角下,其温度系数增大到7.78倍(相对于TT)。而对于方案2,在FF工艺角下,当温度低于60℃时,正温度补偿特性强于负温度补偿特性,输出电压呈现出正温度系数,当温度高于60℃时,正温度补偿特性弱于负温度补偿特性,输出电压呈现出负温度系数,其温度系数增大不到1.4倍(相对于TT)。所以,尽管在典型TT工艺角下,方案1的温度特性优于方案2,但在其他工艺角下,方案2的温度特性整体变化不大,明显优于方案1。因此,方案2表现出较强的工艺健壮性。所以通过选择合适的失配电流和多晶电阻阻值,以适量牺牲典型TT工艺角下的温度系数为代价,可换取工艺稳定性的提高。工艺漂移引起的最大相对变化仅为1.4倍,是最具使用价值的补偿状态。
5 实验结果分析
根据模拟结果,基于无锡上华科技(CSMC)0.18μm CMOS工艺,通过适量牺牲典型TT工艺角下的温度系数,以保证在工艺波动的情况下,其温度系数都处于较好的水平。图3为芯片的显微照片,芯片面积为230μm×290μm。图4给出了在3V电源电压下,-20℃-120℃温度范围内,经修调后的最小温度系数曲线,其值为6.9ppm/℃。可以看出,其温度系数略大于TT工艺角下的模拟数值,基本与FF工艺角下的模拟数值相当。

图3 失配高阶补偿电压基准芯片显微照片

图4 实测带隙基准温度曲线
6 结束语
适当减小高阶失配补偿量和优化多晶电阻阻值,使基于失配电流控制的新型高阶补偿基准电路具有内在的抑制工艺漂移的能力,可实现在较低温度系数下的最佳工艺稳定性。新型补偿基准可实现不同工艺状态下良好的温度特性。因此,提出了一种基于状态工作点失配控制的具有良好工艺健壮性的带隙输出电压源的低成本解决方案。
[1]Y H Lamand,W H Ki.CMOS Bandgap References With Self-Biased Symmetrically Matched Current-Voltage Mirror and Extension of Sub-1-V Design[J].IEEE Trans.Very Large Scale Integr(VLSI)Syst.,2010,18(6):857-865.
[2]Koudounas S,Andreou C M,Geourgiou.A Novel CMOS Bandgap Reference Circuit With Improved High-order Temperature Compensation[C].In:Proceedings of IEEE Industrial Symposium on Circuits and Systems.Pairs,2010:4073-4076.
[3]ILee,G Kim,W Kim.Exponential Curvature-Compensated BiCMOS Bandgap Voltage References[J].IEEE J.Solid-State Circuits,1994,29(11):1396-1403.
[4]PMalcovati,F Maloberti,M Pruzzi,C Fiocchi.Curvature Compensated BiCMOS Bandgap With 1-V Supply Voltage[J].IEEE J.Solid State Circuits,2001,36(7):1076-1081.
[5]G A Rincon-Mora,P E Allen.1.1-V Current-Mode and Piecewise-Linear Curvature-Corrected Bandgap Reference[J].IEEE J.Solid-State Circuits,1998,33(10):1551-1554.
[6]JLi,X Zhang,M Yu.A 1.2-V Piecewise Curvature-Corrected Bandgap Reference in 0.5μm CMOS Process[J].IEEE Trans.Very Large Scale Integr(VLSI)Syst.,2011,19(6):1118-1122.
[7]M D Ker,J S Chen.New Curvature Compensated Technique for CMOS Bandgap Reference With Sub-1-V Operation[J].IEEE Trans.Circuits Syst.II,Analog Digit.Signal Process,2006,53(8):667-671.
[8]K N Leung,P K T Mok.A 2-V 23μA 5.3ppm/℃Curvature Compensated CMOS Bandgap Voltage Reference[J].IEEE J.Solid-State Circuits,2003,38(3):561-564.
[9]Jin Wu,Ning Qu,Weidong Nie,Hao Li.A Simple Curvature Compensated Technique for CMOS Bandgap Voltage Reference[J].IEICE Electro.Exp.,2011,8(17):1374-1379.
[10]吴金,聂卫东,常昌远,等.基于失配控制的非线性补偿带隙基准电路设计[J].东南大学学报(自然科学版),2011,41(5):917-922.
[11]聂卫东,吴金,朱伟民,等.基于混合模式高阶补偿的超低温度系数带隙基准电路[P].中国专利,CN101881986A.2010-11-10.
[12]Y Tsividis.Accurate Analyzes of Temperature Effects in I-V Characteristics with Application to Bandgap Reference Sources[J].IEEE J.Solid State Circuits,1980,15(6):1076-1084.
Process Robust of High-Order Curvature-Com pensated Bandgap Voltage Reference Controlled By Mismatch Current
ZHU Guang-rong1,YIN Dai1,NIEWei-dong1,2,YU Zong-guang2
(1.Wuxi Youda Co.,Ltd.,Wuxi214028,China;2.Department of Electronic Engineering,Jiangnan University,Wuxi214122,China)
The principle of high-order curvature-compensated CMOS bandgap voltage reference controlled bymismatch current is analyzed and the influence of process variation on the temperature coefficient(TC)is studied.The circuit is of the simple structure and high control accuracy.Meanwhile the bandgap reference with low TC and strong process robust is achieved by adjusting the values ofmismatch current and poly resistor.The simulation result shows that the TC in the temperature range of-25℃to 125℃is 4.8ppm/℃with themodel of TT(Typical-Typical),and it is below 9.0ppm/℃with other models.The circuit is fabricated in 0.18μm CMOS process from CSMC and the tested minimum TC,at 3V power supply in the temperature range of-20℃to 120℃,is 6.9ppm/°C which confirms the analysis.
Bandgap reference;High-order curvature-compensated;Temperature coefficient;Process robust
10.3969/j.issn.1002-2279.2014.04.001
TN4
:A
:1002-2279(2014)04-0001-04
朱光荣(1965-),男,江苏姜堰人,硕士,主研方向:模拟电路、半导体工艺与功率器件。
2014-03-19
