一种新的介质滤波器设计方法

卢 青，陈晓光

一种新的介质滤波器设计方法

卢 青，陈晓光

分析并设计了新型介质滤波器结构，提高了滤波器的性能，减小了体积。同时使用 HFSS 电磁仿真软件对所设计的谐振器进行仿真。同时设计了新型的滤波器耦合矩阵综合和优化方法，大大提高了耦合矩阵综合与优化的性能和计算速度。

介质滤波器； 耦合结构； 耦合矩阵综合； 优化算法

0 引言

电磁波在高介电常数的媒介中传播，波长可以缩短，因此可以构成小型的介质滤波器。[1]以往介质滤波器设计过程中一般采用级间耦合的方式，n阶的滤波器需要n个腔体n个谐振器，为了降低成本和减小体积，使用了交叉耦合和多模耦合的方式。新的耦合方式使得耦合矩阵更加复杂，综合更加困难，消耗大量的时间和计算资源。

耦合矩阵的求解和优化是滤波器设计的关键，通过耦合矩阵，可以得到相应的电路结构，从而设计出所需的滤波器。耦合矩阵的求解方法分为两类：一类是矩阵消元法，通过耦合矩阵的消元变化进行求解，但是只适用于一些特定的拓扑结构；另一类是优化算法，通过最优化算法对耦合矩阵进行求解，如梯度优化算法、遗传优化算法。[2]

1 耦合矩阵参数提取流程及公式

耦合矩阵参数提取的流程如图1所示：

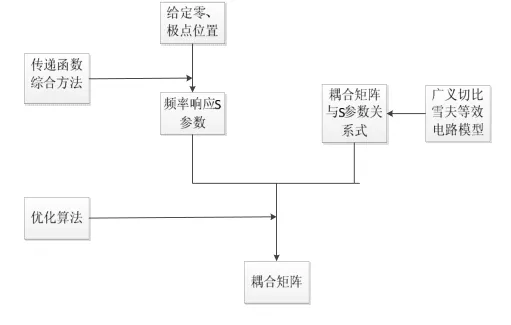
图1：耦合矩阵参数提取流程图

如图所示，交叉耦合滤波器的传输函数是广义切比雪夫多项式[3]，其传输函数的平方可以用公式（1）：

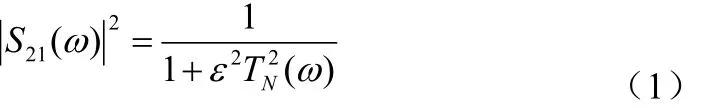
采用迭代方法进行对广义切比雪夫多项式计算求解展开，可得公式（3）、（4）：

2 神经网络优化算法提取耦合矩阵参数

本文中采用了神经网络算法[4-5]，更简捷、有效的计算出微波谐振腔滤波器的高维参数模型。将滤波器结构分解为几部分子结构，对不同的子结构训练其神经网络模型。然后，把不同子结构的神经网络模型组合为最终的滤波器参数模型。这种神经网络算法仅仅需要少量的训练数据，模型建立以后能够准确的求解和优化耦合矩阵参数。

人工神经网络算法（ANN）的研究一定程度上受到了生物学的启发，由一系列简单的单元相互密集的连接构成，ANN 算法能够对分布在大量神经元上的信息表示进行高度的并行处理。

滤波器耦合矩阵需要求解的参数个数为i个，整个模型的输出参数有四个，可以表示为分别是 S11 参数和 S21 参数的实部和虚部。如图2 所示，把整个滤波器分解为 N 个子模块，分别表示为 M1、M2...分解以后，每一个子模块通过独立的 ANN（人工神经网络）算法建模。例如子模块M1拥有三个独立的参数把频率f作为额外的输入变量加上以后，子模块M1拥有四个参数，M1拥有六个输出参数，可以表示为分别是 S11、S21、和 S22 的实部和虚部。其他的子模块和模块 M1 采用同样的处理方法。通过降维处理，每一个子模块所需要消耗的计算资源很小，并且可以通过并行处理每一个子模块，而不用考虑整个模型，大大节省了运算时间.

整个神经网络最小化算法如图2所示：

图2：神经网络算法结构

包含 N个子模块、一个分析模块和频率映射模块。为了把所有的子模块连成一个整体结构，分析模块可以分为以下3个步骤：把子模块的输出（S参数）转化为 ABCD矩阵，然后把所有的 ABCD 矩阵加在一起转化为整体结构的 S 参数。因为高次模在波导中的传播，由神经网络算法转化的S参数结果相比实际的S参数产生了频率漂移的情况。为了修正频率偏移的情况，提出了频率映射模块，其包含一个线性方程代表原始输入的频率，f’表示映射后的频率为线性参数。每一个子模块的ANN算法用来训练得出子模块参数与线性参数之间的关系。d表示电磁仿真的结果，整个算法的目标函数就是为了找到内在的权重参数w使得相应的输出y和d能够最小化误差函数：

其中n是所有的训练样本的数量，Fp是频率点的数量，参数 xk、频率 f和新的映射后的频率 f’之间的映射为：

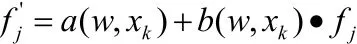
所有子模块在整个最优化过程中都是彼此独立的。

3 利用神经网络算法求解介质滤波器耦合矩阵求解与验证

滤波器的设计指标如表1所示：

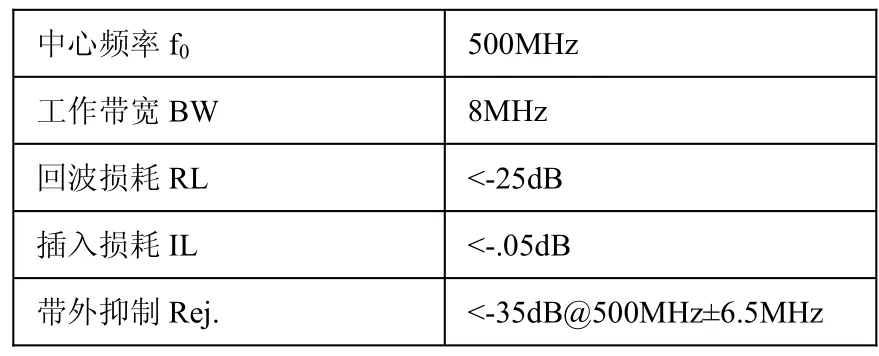
表1 滤波器的设计指标

输入给定滤波器设计指标，运行算法，可以得到满足要求的滤波器的耦合矩阵。

求解出来的滤波器耦合矩阵如下所示：

ADS电路仿真结果如图2所示：

图2 电磁仿真结果

如上图所示，仿真结果与设计指标要求完全符合，证明了算法的有效性。

4 总结

文中在介质滤波器设计过程中采用了神经网络算法来综合滤波器耦合矩阵，大大降低了运算的时间，提高了运算的准确性，并通过电磁仿真验证了模型的有效性。

[1]Zhang Q J, Gupta K C. Neural Networks for RF and Microwave Design (Book+ Neuromodeler Disk)[M]. Artech House, Inc., 2000.

[2]Pozar D M. Microwave engineering[M]. John Wiley & Sons, 2009.

[3]Zhang Q J, Gupta K C, Devabhaktuni V K. Artificial neural networks for RF and microwave design-from theory to practice[J]. Microwave Theory and Techniques, IEEE Transactions on, 2003, 51(4): 1339-1350.

[4]Burrascano P, Fiori S, Mongiardo M. A review of artificial neural networks applications in microwave computer‐aided design (invited article)[J]. International Journal of RF and Microwave Computer‐Aided Engineering, 1999, 9(3): 158-174.

[5]J.K. Plourde and C. Ren, “Application of Dielectric Resonators in Microwave Components”, IEEE Trans. Microwave Theory Tech., Vol. MTT-29, pp. 754–769, August 1981.

A Novel Method of Dielectric Resonator Filter Design

Lu Qing, Chen Xiaoguang
(College of Information Science and Engineering, Fudan University, Shanghai 200433, China)

This paper presents a simple and efficient high-dimensional parametric model of dielectric resonator filter utilizing a modular neural network technique. This method completes cross-coupling synthesis quickly and designs a coaxial filter with this method. With the development of filter design, microwave filter is not difficult overall, the future of dielectric resonator filter design focuses on the fast simulation technology and automated tuning technology.

Dielectric Filter; Cross-Coupling; Cross-Coupling Matrix Synthesis; Optimization Algorithm

TP311

A

1007-757X(2014)02-0057-02

2014.02.28)

卢 青（1988-），男，江苏省宿迁人，复旦大学，在读硕士研究生，研究方向：电磁场与微波，上海，200433陈晓光（1964-），男，复旦大学，副教授，研究方向：无线通信、电磁场与微波，上海，200433