具有输入饱和的环形永磁力矩电动机伺服系统自适应反步控制

蔡建平

(浙江水利水电学院 应用数学研究所，浙江 杭州 310018)

0 引 言

高性能电机被广泛应用于高科技、高精密的现性系统自适应控制研究.代化制造业当中，如工业系统、精密加工过程等.伴随着高性能电机的广泛应用电机系统的控制研究越来越受到科研工作者的重视.在实际系统运行中，因为未知扰动、未知摩擦、未知推力波动等不确定性[1-4]的存在使得被控系统的性能大受影响.特别是对电机速度控制性能的影响及由此所产生的机械震动将会导致系统性能的严重下降.环形永磁力矩电动机属三相永磁同步电动机，其特点是直接驱动，并且具有大直径长度比、多极数等优点[5].电动机本身对最大电流的限制使得电机输入呈现出饱和特性.环形永磁力矩电动机输入饱和的存在使得被控系统的性能受到很大影响，甚至会导致系统不稳定[6].为提高系统的性能和可靠性，电机系统的控制设计中必须考虑未知输入饱和.在具有输入饱和的电机系统的控制器设计中，常用的方法有针对精确系统的低-高增益混合控制器设计[7-8]、抗饱和补偿器的设计及应用[9-10]等.由于精确系统常常难以获得，系统建模过程中的各种不确定因素使得模型中存在各种不确定性.为了使控制器的设计更能与实际被控系统相契合，在控制器设计中充分考虑系统不确定性是合理的.

本文针对含有未知参数的环形永磁力矩电动机系统，并考虑系统具有未知输入饱和，应用Backstepping控制器设计方法设计自适应控制器，保持系统稳定.同时系统中还考虑了未知扰动的存在，同样通过对未知扰动的常数上界的自适应估计，在控制器设计中引入基于扰动上界的估计值的相关项对未知扰动的不确定性影响进行补偿.与文献[11]相比，本文中提出的自适应控制器不再要求系统未知参数的界已知，同时充分考虑了系统未知外界扰动.最后仿真结果也进一步验证了本文设计的Backstepping自适应控制器的有效性.

1 系统描述

考虑如下环形永磁力矩电动机的运动方程[11]

(1)

其中J为系统转动惯量，ω是转子角，电磁转矩为Te，齿槽转矩表示为Tc.B是表征负载阻尼和粘性摩擦的系数,d(t)表示其他所有的有界的外界扰动.电磁转矩可表示为

Te=KTiq

(2)

其中KT为转矩系数，iq表示转动轴电流.考虑到齿槽转矩与转子位置θ及基波之间的下述关系

(3)

Tc=AcSc(θ)

(4)

其中，Ti为i次谐波的齿槽转矩峰值，Nc为定子齿数与极数的公倍数，Ksk为斜槽系数.Ac为未知函数，Sc(θ)是已知函数表示齿槽转矩基波的形态函数.

令状态变量x1=θ;x2=ω,系统方程可重写为如下二阶系统

(5)

(6)

其中常数uM为饱和界.控制器设计前需如下假设：

假设1.系统输入输出稳定.

假设2.参考输出信号yr及其1,2阶导数均有界.

2 控制器设计与稳定性分析

本节将讨论如何设计控制器以保证系统稳定，并且实现系统跟踪性能.为了对饱和的影响作出补偿，类似于[12]首先引入辅助信号

(7)

其中c1，c2为大于0的常数，Δu=u(v)-v.

系统控制器设计前先做如下坐标变换

(8)

其中z1表示跟踪误差，α1表示在第一步中的虚拟控制．下面将利用backstepping方法设计控制器.

第一步：由(8)及系统方程(5)可得

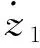
=z2+α1+c1γ1

(9)

取

α1=-c1(z1+γ1)

(10)

其中c1>0为常数,取Lyapunov函数为

(11)

对该Lyapunov函数求导数可得

(12)

第二步：由(8)及系统方程(5)可得

(13)

取控制信号

(14)

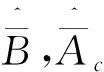
(15)

其中ηD为正设计参数.参数估计误差表示为

对该Lyapunov函数求导数可得

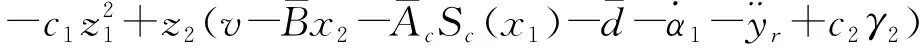
(16)

参数的估计率取为

(18)

则可得Lyapunov函数的导数为

(19)

定理1：对于环形永磁力矩电动机系统(1),系统饱和输入由(6)给出.在控制输入(14)及参数估计率(18)的作用下，闭环系统全局稳定.

证明：显见，由(18)可知闭环系统信号x1,x2,z1,z2有界，进一步得虚拟控制信号有界，控制输入信号有界.则可建得闭环系统所有信号有界.

3 仿 真

仿真中采用与孙宜标等[11]同样的电机系统,其各系统参数取值如下:Ten=232N·m，转矩系数KT=9.4 N·m/A，转动惯量J=0.205 kg·m2，额定电流In=42.1 A，B=0.09 N·m·rad/s.外界扰动取为0.1sint,参考信号yr=sin(2πt).由上述电机参数计算得卡槽转矩Tc=6sin(180x1)N·m.饱和输入的电流限制值为40A.仿真中设计参数取为：ηD=ηB=ηA=1，c1=c2=15.仿真中所有信号的初始值均取为0.仿真图形如下，图1给出跟踪误差曲线图.由该图可以看出，输出信号能再短时间内实现对参考信号的跟踪，但由于控制输入的饱和特性使得精确跟踪很难实现.图2给出的是控制信号v的时间曲线图形，该控制信号是我们设计的输入信号，并不直接作用于被控系统，通过饱和非线性变换得到直接作用于系统的输入信号u由图3给出.通过仿真图形可以明显看出该控制器可以保持系统稳定，同时也可以实现对参考信号的跟踪.

4 结 论

针对具有输入饱和的环形永磁力矩电动机伺服系统,应用反步方法设计自适应控制器.该控制器在饱和输入下能对未知外界扰动进行有效补偿，保持系统稳定.同时实现了控制输出对指令信号的快速跟踪,且具有很好的鲁棒性.仿真实验进一步验证了控制器的有效性.

参考文献：

[1] 孙宜标，闫 峰，刘春芳.基于μ理论的永磁直线同步电机鲁棒重复控制[J].中国电机工程学报,2009,29(30):52-57.

[2] BIN YAO, LI XU. Adaptive robust motion control of linear motors for precision manufacturing[J]. Mechatronics,2002(12):595-616.

[3] 刘 雨，苏宝库，曾 鸣.一种改善无刷直流电机动系统速率平稳性的鲁棒重复控制方法[J].中国电机工程学报,2005,25(10):144-148.

[4] 杨 松,曾 鸣,苏宝库.一种改进的基于分解控制的非线性力矩补偿策略及其在直流电机系统中的应用[J].航空学报,2007,28(2):365-369.

[5] 王成元，夏加宽，杨俊友，等．电动机现代控制技术[M]．北京:机械工业出版社，2006．

[6] JANG J O. Neural network saturation compensation for DC motor systems[J]．IEEE Trans．on Industrial Electronics，2007，54 (3):1763-1767．

[7] MARCHAND N，HABLY A．Global stabilization of multiple integrators with bounded controls[J]．Automatica，2005，41(12): 2147-2152．

[8] ZHOU B，DUAN G R．A novel nested nonlinear feedback for global stabilization of linear systems with bounded control[J]．International Journal of Control，2008，81(9) :1352-1363．

[9] PHIL MARCH，MATTHEW C TURNER． Anti-windup compensator designs for non-salient permanent-magnet synchronous motor speed regulators[J]． IEEE Trans． on Industry Application，2009，45(5):1598-1608．

[10] 杨 明，李 钊，胡 浩，等．永磁同步伺服系统速度调节器抗饱和补偿器设计[J]．电动机与控制学报，2011，15(4):46-51．

[11] 孙宜标，刘春丽，王丽梅．具有输入饱和的环形永磁力矩电动机自适应鲁棒控制[J]．制造技术与基础，2011(12):94-98.

[12] J. ZHOU, C. WEN. Adaptive Backstepping Control of Uncertain Systems [M]. Verlag Berlin Heidelberg, Springer, 2007.