脉冲神经网络自适应侧连接的运动检测

刘海华，庄如云

(中南民族大学 生物医学工程学院，武汉430074)

模拟视觉系统的信息处理机制进行运动检测和动作识别一直是计算机视觉中的重要研究领域.随着神经生物学研究的不断深入，使得人们对视觉系统的理解更深刻，从而使模拟视觉系统的工程应用也取得了长足的进步.初级视皮层(V1)作为视觉系统信息处理的“必经之路”[1]，为视觉通路中更高层信息处理区域(如MT，IT等)提供了有效的信息传递.因此，模拟V1神经网络的信息处理研究对于运动检测、动作识别等有着重大意义.

Wiese和Hubei于1959年对猫的大脑视觉皮层研究发现，V1中大部分神经元感受野对于特定方向的边缘有较强响应[2]，在此研究成果基础上，研究者提出了V1细胞对时空信息检测的生理学模型[3]，表达了神经元在方向、速度选择性的调制功能[4].根据这些前期理论，Giese and Poggio提出了视觉信息处理的神经元前馈层次结构模型[5].然而，这些研究只是注重模拟V1单个神经元生理学特性的时空信息检测，而没有全面考虑不同视觉区域或同一区域不同神经元之间的相互作用，从而导致时空检测效果的不理想.由于V1中神经元之间通过突出和树突相互连接，这种连接称之为侧连接，每个神经元的特性将直接影响到其相邻神经元的特性.生物学实验证明它的存在性和功能，表明了V1神经元之间的大范围侧连接是V1细胞群对刺激选择的中介[6]，且具有优先方向性[7]，因而需要关注神经元之间内在联系的整体特性[8].神经元之间侧连接在整体上表现为中心环绕的相互作用特性，该特性具有环绕抑制和易化两种功能.基于该现象，研究者提出了许多模型[9，10].但这些模型只是建立在神经生理学上的，并没有用于实际的运动信息检测中.为此，本文模拟初级视觉皮层脉冲神经网络，提出了自适应侧连接的运动检测方法，给出侧连接的范围和强度的计算方法，以实现运动信息的有效检测.

1 神经元与侧连接

大量证据表明神经元突触任意发展，神经元之间容易相互影响[11]，这使得脉冲神经网络的分析和仿真比较困难.为此，本文采用从简单到复杂的方法进行分析，从而实现运动信息的检测.

对于单一神经元研究者提出了许多种模型，虽然这些模型在计算方法上有所差异，但总体的生物学属性得到了体现.为此，本文利用LIF(Leaky Integrate-Fire)模型[12]，表达了脉冲神经元在外界激励下的行为，其形式如式(1):

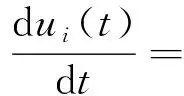
gL(VL-ui(t))+Ii(t)，

(1)

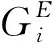
对于神经元之间的连接，假设神经元均匀分布，它们之间有相互作用，其相互作用强度决于分布的位置.换句话说，经元之间连接的权重与神经元分布位置有关，其侧连接关系如图1所示.

图1 神经元侧连接关系图Fig.1 The representation of the neural network in cortical layer

1.1 神经元输入与环绕抑制

V1细胞分为两种，即简单细胞和复杂细胞.V1简单细胞感受野对于空间刺激的响应行为可以通过2D-Gabor函数来描述.对于视频激励的响应行为可采用3D-Gabor滤波器gv,θ,φ(x,y,t)来描述[13].则简单细胞对输入刺激I(x,y,t)的响应为：

rv,θ,φ(x,y,t)=|I(x,y,t)*gv,θ,φ(x,y,t)|+,

(2)

其中*为卷积符号，|.|+为半波整流且被定义为：

(3)

3D-Gabor滤波器可以表示为：

(4)

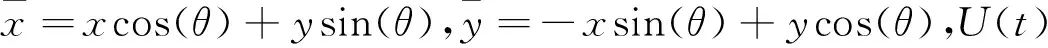
复杂细胞的响应通常为简单细胞响应的非线性组合[13].复杂细胞的反应与刺激感受野的精确位置相对独立，具有相位不敏感性，则其响应为：

(5)

该响应被称为运动能量.

对于每个神经元位置，除有上述的兴奋性神经元外，还有耦合的抑制性神经元[14].为了描述其整体响应，在该空间上需要考虑其抑制性作用.考虑局部环绕抑制作用，则其在空间位置上的整体响应为：

Rv,(θ)(x,y,t)=|Ev,(θ)(x,y,t)-αSv,(θ)(x,y,t)|+,

(6)

其中α为环绕抑制因子，控制环绕抑制强度.Sv,(θ)(x,y,t) 为环绕单元，表示为：

Sv,(θ)(x,y,t)=SEv,(θ)(x,y,t)*wv,(θ)(x,y,t),

(7)

式(7)中wv,(θ)(x,y,t)为环绕权重函数，文献[3]给出了其定义.

由于Rv,(θ)(x,y,t)为局部环绕抑制运动能量，获得了神经元在该空间位置上刺激的感知.感知的运动能量将作为IF模型中神经元的输入电流Ii(t)，其形式为：

(8)

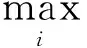
1.2 侧连接

细胞的响应是由激励引起的，该激励除了来自外侧膝状体(LGN)神经元所传入的激励外，还有来自相连神经元的响应，其侧连接的结构如图1所示.由于局部环绕抑制在上节中已经参与了计算，因此，在图1的结构中没有自连接.

由图1可见，每个脉冲神经元除了输入电流外，还与许多神经元连接.该连接对神经元的作用可以利用兴奋和抑制电导来反映[12]，其计算公式为：

(9)

(10)

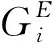
(11)

其中sgn(q)是一个符号函数，

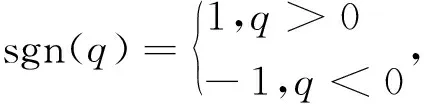
Ci(x,y)=Rδ×Wσ,θ(x,y),

(12)

式中Rδ定义为侧连接的方形邻域范围，Wσ,θ(x,y)为2D-Gabor函数：

(13)

图2 不同方向神经元空间邻域侧连接加权系数关系Fig.2 Lateral connect weighting factor of neurons in different directions spatial neighborhood

β(t)为时间衰减指数，其定义为[12]：

(14)

式(14)中ε(t)为单位阶跃函数，τs为时间常数，兴奋的时间常数(τE=0.6ms，达峰时间为3ms)比抑制的时间常数(τI=1.0ms，达峰时间为5ms)少[12].这里为了简化计算，暂时不考虑时间衰减，因为模型主要是证明侧连接的有效性.

1.3 自适应侧连接

虽然神经元的响应与神经元的侧连接有较大的关系，但是神经生理学研究表明，侧连接的范围与外界刺激有较大的关系.Tidan研究表明对某神经元的刺激能量越大，其受影响的范围越小，即越邻近的神经元对其产生抑制性越大；当刺激能量弱时，其受影响的范围越大，即周围神经元对其产生兴奋性越大[15].针对这一特性，提出了一个简单的自适应方法来对视觉神经元侧连接相互作用进行模拟.

首先，考虑刺激强度对神经元侧连接范围的作用.刺激强度直接由视频图像的对比度决定，对比度高，则刺激强.而式(5)的运动能量直接反映了细胞所受刺激的强度，因此，刺激强度由运动能量图的对比度确定.根据Weber关于非周期刺激的对比度定义[16]：

Cw=(Lo-Lb)/Lb,

(15)

式(15)中Cw表示目标对比度，Lo表示目标点灰度值，Lb表示背景灰度值.Contrast为视场中Cw值的线性归一化结果.

为了计算简单，设置4个对比度级：0～A、A～C、C～B和B～1.对应这些对比度的侧连接模板大小为Radp={R0,Rl,Rh,R1}，这些值随着对比度的增加而变小.

其次，随不同刺激所引起的侧连接区域范围不同，其连接强度也有所不同，所以计算兴奋电导和抑制电导的加权公式需更新，即连接强度为：

Ci(x,y)=Radp×Wadp(σ,θ)(x,y),

(16)

(17)

由(17)式可见，由于A、B、C为常数，表示对比度级值.当对比度大于B，小于A时，由于对比度极强或极弱，因此不考虑侧连接，则其加权强度为0，因而不需考虑模板大小；当对比度在A～C和C～B内时，对比度小于C说明该位置上细胞能量比较弱，需要加重侧连接的影响，所以利用较大的侧连接模板，对比度大于C说明位置上细胞能量比较强，需利用比较小的侧连接模板，并且相应不同模板的加权系数也将随之改变.本文为了简单起见分别设置为Rl=5×5，对应该模板大小的系数为Wl；Rh=3×3，对应模板大小的系数为Wh.

2 实验结果与分析

为了验证本文所提出的理论和方法，在PC机上利用Matlab软件工具进行了实现，并利用模拟数据分析本文理论和方法的合理性以及确定提及的参数设置，最终定性分析对真实数据的处理结果.

2.1 不同对比度的运动信息检测

根据自适应侧连接的原理，对于低对比度的刺激可以产生较大的模板，当在其同方向有较强的刺激时，将对该神经元产生易化作用，从而提升对低对比度的运动信息检测.为此，采用模拟数据的方法进行实验.

首先检测对比度不一致杆子的运动，如图3所示.该杆子以4pps(每秒4个像素)的速度沿水平方向运动.其中杆子中间有一段对比度为其它部分对比度20%的部分，长度分别为3、9、15个像素点.由于其对比度较低，因此在低对比度下模板大小为5×5个神经元，自适应侧连接的参数设置为A=0.15，B=0.8，C=0.4.实验结果如图3所示.

从图3可见，局部环绕抑制可以提升小范围低对比度的运动检测，当低对比度范围增大时，其作用变得很小.而自适应侧连接对加大范围的低对比度运动检测的提升非常明显.出现这种现象的主要原因是，低对比度为3个像素时没有超出细胞经典感受野的范围，所以即使不加如侧连接，该部分的运动检测也得以提升.而当低对比度的范围增大为9个像素时，因超过了细胞经典感受野的范围，不能完全提升所有范围内的运动检测，从而出现了断点.当加入侧连接的运动检测断点减少，但杆子变粗.然而当加入自适应侧连接时，低对比度运动检测较完整，且没有出现杆子变粗的现象，这一点在低对比度范围为15个像素的情况下效果更明显.

图3 运动信息检测Fig.3 Motion detection

为了进一步验证自适应侧连接对运动检测性能的影响，分析在不同的侧连接模板下对比度的变化与响应结果之间的关系.我们利用明暗两根不同对比度的杆子作为刺激，其暗杆子的对比度为亮杆子对比度的20%，自适应侧连接的参数设置为A=0.15，B=0.8，C=0.4，实验结果如图4所示.

从实验结果可以看出，自适应侧连接对低对比度运动检测的效果与未加侧连接的结果相比有十分明显的提升，而与非自适应侧连接对于低对比度运动检测效果相比也有很大的改善.产生这种效果的主要原因是，非自适应侧连接对于所有神经元都加入了兴奋(或抑制)电导，所以无论是对比度如何都得到了同样的提升(或抑制)，这样就使得低对比度运动检测没有得到明显的提升；而自适应侧连接对于低对比度运动检测由于增大了侧连接影响的范围，其效果受神经元更多同属性质激励的影响，所以自适应侧连接对于低对比度运动部分检测效果明显.

为了定性地、定量地分析自适应侧连接对不同对比度运动的检测，采用具有不同对比度的运动对象作为刺激，根据所提出的自适应侧连接的方法获取神经元的膜电压值，如图4所示.讨论分析所获数据，验证所提理论方法，其中自适应侧连接的参数设置为A=0.15，B=0.8，C=0.4 .

图4 不同对比度运动对象的运动检测Fig.4 Motion detection in different contrast

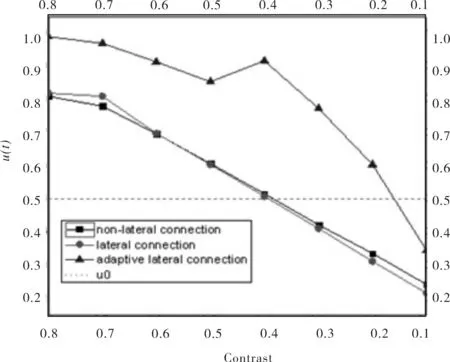
图5 不同对比度运动检测的数据分析曲线Fig.5 Data analysis curve of motion detection in different contrast

从图4的实验结果可见，采用自适应侧连接的方法可以较大程度地提升对于低对比度运动对象的检测.从定量的角度，图5给出了不同方法对不同对比度运动对象的检测结果.由此发现，当对比度逐渐下降，神经元膜电压值下降，但不同方法下降的程度不同.在给定膜电位阈值的情况下(图5中阈值为0.5)，自适应侧连接方法在较低对比度刺激情况下所获神经元膜电压值仍比阈值高，神经元仍能产生发放，因此保证了低对比度运动对象的检测.

2.2 不同噪声环境下的运动检测

为了验证侧连接对不同噪声环境下运动检测的作用，采用一组人工合成视频进行试验，如图6所示.柱状刺激物以4pps的速度沿水平方向运动，且视频序列中加入了大量的高斯噪声.为了描述高斯噪声程度，采用其方差作为噪声因子，其中图6序列中的噪声因子为0.15.自适应侧连接的参数设置为A=0.3，B=0.8，C=0.4 .

图6 噪声环境下的运动检测Fig.6 Motion detection in noise environments

从图6第3～5行细胞响应能量图可以发现，加入侧连接之后对于噪声的抑制效果较好，增强了对运动信息的检测.为了定量地分析侧连接对于噪声抑制的效果，通过计算不包括刺激对象的所有区域中噪声响应和来评估其性能.实验分别对不同噪声因子的视频序列进行操作，其方法采用不同的侧连接模式进行操作.由于序列中噪声为随机高斯噪声，为了减少实验结果的随机性，采用多帧图像噪声响应的平均值进行计算，本实验采用15帧噪声响应总和平均，实验结果如图7所示.

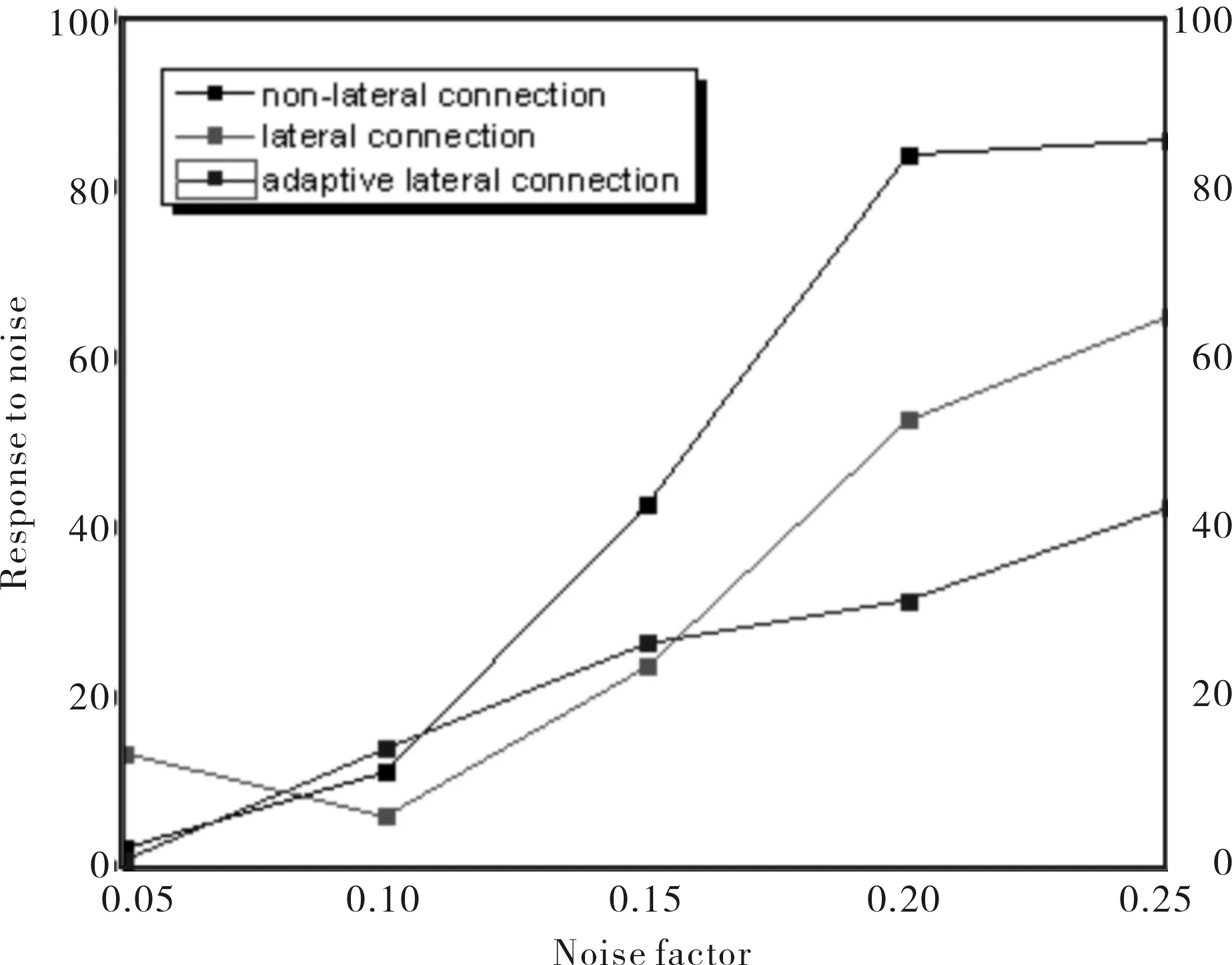
图7 不同侧连接方法对噪声抑制的效果Fig.7 Noise suppression effect of different lateral connect

从图7可以看出，在噪声因子为0.1之前，侧连接的加入对噪声的抑制效果影响不大，这主要是由于噪声强度不大，在运动能量提取过程中局部中心环绕抑制对噪声的抑制已有较好的效果，加入侧连接反而可能将剩余噪声放大；当噪声因子大于0.1时，由于局部中心环绕抑制不能很好地抑制高强度的噪声，加入侧连接扩大抑制范围，从而很好的抑制了噪声；从实验结果还可以看到自适应侧连接对于噪声的抑制效果在高噪声情况下为最优的.

2.3 视频运动检测

为了检验自适应侧连接方法对实际运动对象的运动检测效果，选择了公开的KTH视频数据库进行实验.实验结果如图8所示.

图8(a)给出运动对象与背景之间的对比度比较明显，由于产生的环绕抑制运动能量较强，加入侧连接方法对神经元膜电位图所产生的变化不大.图8(b)给出了运动物体与背景之间对比度比较低，产生的环绕抑制运动能量也比较弱，而且在背景部分还产生了一些噪声.从环绕抑制运动能量图可发现在背景中有明显噪声点；而当采用侧连接方法时，神经元的膜电位图中由噪声点所引起的响应较少，但对于低对比度的运动检测不明显；但采用自适应侧连接方法时，神经元的膜电位图能观察到由噪声所引起的响应进一步减少，且更稀疏，几乎都被去掉了，且对对比度较低的运动检测更明显.由此可以得出这样的结论，侧连接方法对于背景噪声的去除、对低对比度运动检测效果十分明显.

3 结语

侧连接是视觉皮层神经网络的基本机制，基于该机制，本文提出了自适应侧连接的运动检测方法.该方法根据刺激强度的不同，神经元相互作用也随之变化，从而建立了神经元自适应侧连接方法.通过实验发现自适应侧连接方法对于噪声抑制效果优于其它方法.这主要是因为自适应侧连接相互作用的范围是随刺激强度的变化而变化的，即对于较强的刺激其相互作用的范围较小，而对于强度较弱的刺激其相互作用的范围较大，这不仅符合了神经元相互作用的生理实验数据，而且对噪声抑制有较好的效果，而且对不同对比度的运动刺激的检测有较好的性能.然而本文提出的方法将刺激强度只作了初步的划分，划分的级数并不多，且划分值主要是采用经验值，而不同的序列、同一序列中不同图像的对比度、噪声强度是不同的，如何使本文建议的方法具有更强的自适应能力，有待进一步研究.

参 考 文 献

[1] Escobar M J, Masson G S, Vieville T, et al. Action recognition using a bio-inspired feedforward spiking network[J]. International Journal of Computer Vision, 2009, 82(3): 284-301.

[2] 寿天德.视觉信息处理的脑机制[M].合肥：中国科学技术大学出版社,1997：12.

[3] 黄丽鸿, 谌先敢, 刘海华. 模拟初级视皮层脉冲神经元的动作识别系统[J]. 自动化学报, 2012, 38(012): 1975-1984.

[4] Simoncelli E P, Heeger D J. A model of neuronal responses in visual area MT[J]. Vision Research, 1998, 38(5): 743-761.

[5] Escobar M J, Masson G S, Vieville T, et al. Action recognition using a bio-inspired feedforward spiking network[J]. International Journal of Computer Vision, 2009, 82(3): 284-301.

[6] Gilbert C D, Wiesel T N. Clustered intrinsic connections in cat visual cortex[J]. The Journal of Neuroscience, 1983, 3(5): 1116-1133.

[7] Van Hooser S D, Heimel J A, Chung S, et al. Lack of patchy horizontal connectivity in primary visual cortex of a mammal without orientation maps[J]. The Journal of Neuroscience, 2006, 26(29): 7680-7692.

[8] McLaughlin D, Shapley R, Shelley M, et al. A neuronal network model of macaque primary visual cortex (V1): Orientation selectivity and dynamics in the input layer 4Cα[J]. Proceedings of the National Academy of Sciences, 2000, 97(14): 8087-8092.

[9] Buzás P, Kovács K, Ferecskó A S, et al. Model‐based analysis of excitatory lateral connections in the visual cortex[J]. Journal of Comparative Neurology, 2006, 499(6): 861-881.

[10] Hunt J J, Bosking W H, Goodhill G J. Statistical structure of lateral connections in the primary visual cortex[J]. Neural Systems and Circuits, 2011, 1(1): 3.

[11] Arkachar P, Wagh M D. Criticality of lateral inhibition for edge enhancement in neural systems[J]. Neurocomputing, 2007, 70(4): 991-999.

[12] Wielaard D J, Shelley M, McLaughlin D, et al. How simple cells are made in a nonlinear network model of the visual cortex[J]. The Journal of Neuroscience, 2001, 21(14): 5203-5211.

[13] Petkov N, Subramanian E. Motion detection, noise reduction, texture suppression, and contour enhancement by spatiotemporal Gabor filters with surround inhibition[J]. Biological Cybernetics, 2007, 97(5-6): 423-439.

[14] Stettler D D, Das A, Bennett J, et al. Lateral connectivity and contextual interactions in macaque primary visual cortex[J]. Neuron, 2002, 36(4): 739-750.

[15] Levitt J B, Lund J S. Contrast dependence of contextual effects in primate visual cortex[J]. Nature, 1997, 387(6628): 73-76.

[16] Shapley R, Enroth-Cugell C. Visual adaptation and retinal gain controls[J]. Progress in Retinal Research, 1984, 3: 263-346.