遗传算法支持下土地利用空间分形特征尺度域的识别
2014-08-04史文中陈晓玲付东杰
吴 浩,李 岩,史文中,陈晓玲,付东杰
(1.武汉理工大学资源与环境工程学院,武汉430070;2.香港理工大学土地测量与地理资讯学系,香港999077;3.武汉大学测绘遥感信息工程国家重点实验室,武汉430079;4.中国科学院地理科学与资源研究所,北京100101)
土地利用研究是生态学与地理学交叉研究的热点问题之一,也是当前全球变化研究的重要组成部分[1]。深入准确了解土地利用空间结构特征,有助于全面掌握土地利用格局,达到科学合理地配置有限土地资源目的[2]。分形几何理论主要用于描述空间对象的不规则自相似特征,在定量表达复杂的空间格局方面具有一定优势,近20多年来它已经成为国内外学者研究土地利用的重要方法之一[3-8]。但是,土地利用的空间自相似分形特征只存在于特定的空间尺度范围内,超出某个范围来讨论分形维数没有意义,这个范围就是分形维数的无标度区间,对于土地利用空间特征来说就是分形特征存在的尺度域[9]。因此,准确识别分形特征的尺度域是应用分形理论来研究土地利用空间分形格局的前提条件。
无标度区间的求解一直以来都是分形几何理论研究的重要方向。传统的人工判断法和三折线法,以空间离散点分布趋势作为出发点,凭经验来判断分形无标度区间上下界或者有效的中间段,缺乏明确客观的理论依据,存在着主观性较强和误差较大的缺点。此后,Yokoya等以线性回归理论为基础,提出了相关系数法和强化系数法,但是上限的选取对计算的结果影响较为敏感,在应用中存在一定的局限性[10]。党建武等采用遗传编程方法,给出了一种关联维算法来用于识别分形无标度区间的范围,较适用于无标度区较窄的情况,需要一定的人工干预[9]。苟学强等提出利用小波变换的多尺度微分特性,通过对系统性弯曲的多尺度识别来计算出无标度区间范围。但是缺乏对搜索检验标准进行明确的讨论,包括相关系数显著性的检验、拟合标准差和剔除异常点等问题[11]。蔡金华等根据Richardson曲线的“反S”特征形成规律,提出采用基于反S的数学模型的无标度区自动确定方法,用于地图目标分形无标度区间的识别,因其要求观测尺度必须具有足够宽的取值范围才能进行识别运算,所以不具备较强的广泛应用性[12]。由此可见,无标度区间的求解方法很多,且因领域不同也存在差异性。对于遗传算法来说,其用于无标度区解算的相关研究也取得了积极的进展。陈遵德依据自动确定无标度区原则,采用多段折线最优逼近方法找到标度不变区,并引入遗传算法找到全局(或近似)最优解,从而提高了确定无标度区的计算速度[13];费斌等提出了一种基于遗传算法截取无标度区间的方法,并将此方法应用于磨削表面的分形研究,证明在获得同等精度的计算结果条件下,大大缩短了无标度区间计算时间[14];巫兆聪在系统分析上述两类无标度区间识别方法的缺点后,提出基于标准偏差的自适应无标度区确定方法,并初步引入遗传算法进行对比分析,以验证其有效性;但是遗传算法随机产生的种子可能存在负值,结果缺乏稳定性[15]。范玉红利用分形插值理论模拟了塌陷区的分形地形生成,并引入遗传算法进行无标度区间最优解和分形特征参数的求解[16]。虽然上述无标度区间识别方法主要是针对一些特定领域来展开算法设计,但已经证明遗传算法在识别无标度区间上具有一定的潜力,然而对于土地利用这一类空间尺度特征尤为显著的问题来说,需要引入能够适应遥感影像的大尺度范围的分析策略[15],并根据土地利用空间格局实际分析的需要,对适应度函数和遗传算子开展针对性设计,才能确保无标度区间的快速精确寻优。
本文以武汉市武昌区水域半径维数的计算为例,应用遗传算法来计算分形维数的无标度区间范围,并同传统的方法进行对比,验证其识别土地利用空间分形特征尺度域的优势,有助于客观地理解城市土地利用空间格局,进而指导土地利用规划的修编,辅助城市土地利用规划以达到用地合理配置目的。
1 研究区与数据
1.1 研究区域概况
本文所选择的研究区域是武汉市武昌区(图1),地处武汉市城区东南部,位于长江南岸,与汉口、汉阳隔江相望,北至余家头罗家港与青山区毗邻;东、南与洪山区洪山乡、青菱乡交错接壤,西临长江。全区面积82.4 km2,户籍人口达100.34万,是武汉市人口最为稠密的行政区。其辖区除长江外,还有中国最大的城中湖东湖和大型濒江湖泊沙湖,水域是其最重要的土地利用类型。这些水域不仅能够丰富城市景观格局,还可在防涝减灾、减缓城市热岛效应和保护生物多样性等方面发挥重要的作用[17]。但是,自20个世纪90年代以来,人为活动对武昌区水域的空间分布影响较大,水域空间格局特征的快速变化和生态功能的严重退化,已经得到2009年第13届世界湖泊大会等国内外学术组织机构的广泛关注。
1.2 数据来源与预处理
本文选取武汉市武昌区2012年3月27日获取的无云Quickbird多光谱遥感影像,其多光谱空间分辨率为2.4 m。根据遥感图像的可识别度及武昌区地域性等基本原则,参照中东部地区生态环境现状遥感调查土地利用/土地覆被分类系统[18],采用决策树方法结合监督分类方法对影像进行分类,结合由影像提取出的植被指数和监督分类的初步结果,将武昌区的土地划分为未利用地、林地、农业用地、水域、草地和建设用地六种地类(图2)。其分类结果经精度验证,该影像分类的总体精度为87.5%,能够满足后续土地利用分形维数的计算精度。
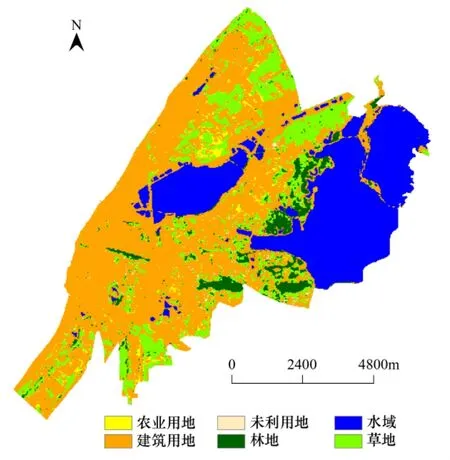
图2 武昌区土地利用分类结果Fig.2 Land use classification results of Wuchang district
在上述处理基础上,以武昌区几何中心为圆心,利用ArcGIS软件以等间隔逐渐递增的尺度为半径建立分级同心圆,从而形成缓冲区来切割土地利用分类图,以提取水域用地在不同半径范围内的面积数据,作为分形维数计算的基础。
2 研究方法
遗传算法是借鉴生物界自然选择和自然遗传机制的优化随机搜索算法,它采纳了自然进化过程中的选择、交叉、变异、迁移等模型[19],通过在搜索过程中自动获取和积累有关搜索空间的知识,控制自适应搜索过程,得到最优解或准最优解,具有简单、通用以及鲁棒性强等特点[20]。
2.1 流程思路
利用遗传算法来识别土地利用空间分形特征尺度域,其主要思路是:首先利用遥感影像提取土地利用分类信息,并统计出不同尺度内各类用地的面积;然后建立不同尺度范围下的水域半径r-面积s的双对数散点映射关系;接着通过设计合理的适应度函数和有效的遗传算子,运用遗传算法来计算水域分形特征的尺度域;最后利用位于该尺度域范围内的离散点,计算出半径维数。
遗传算法的设计是求取水域用地空间分形特征尺度域的关键所在(图3),其核心内容包括参数编码、初始群体的设定、适应度函数的设计、遗传算子设计4个方面[20]。对不同尺度下的水域参数进行二进制编码,依据随机产生的初始种群,计算各个体的适应度,并判断是否符合优化标准。若符合,则输出最佳个体及其代表的最优解,并结束计算;否则,根据适应度选择再生个体,此时适应度较高的个体被选中的概率较高,而适应度低的个体则有可能被淘汰[21]。其中,新生成的个体是根据土地利用分形维数计算的需要,设计其交叉和变异的概率数值大小及优化方法,以便产生新一代的种群,然后返回计算适应度,如此循环直到输出最优个体为止。
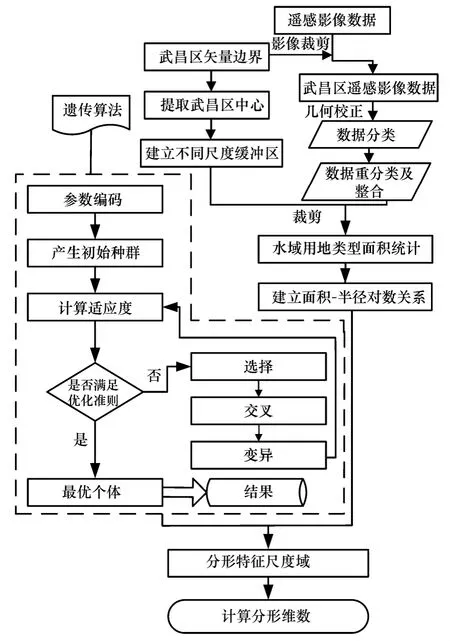
图3 整体流程图Fig.3 The overall flow chart
2.2 适应度函数
适应度函数的设计对运用遗传算法来识别土地利用空间分形特征尺度域至关重要,它是进行遗传操作中选择算子的前提。适应度越大表示离散点连续区间越好,也表示分形维数的存在是有意义的;反之适应度越小,则对应的离散点连续区间越差,其分形维数存在的意义不大。所以,根据适应度的大小对离散点对应的连续区间来进行选择,才能保证适应性能较好的连续区间有更多的机会进行循环,从而计算出正确的无标度区间,即分形特征的尺度域。
本文是以无标度区间离散点拟合的离差平方和平均值最小作为目标函数,原则是其目标值越小所对应的适配值越大,此时该个体就优越。由于适应度函数的设计通常求取最大值,而此时目标函数的离差平方和平均值为最小,故设计如下适应度函数:

式中,G是位于某一连续区间内离散点的实测值和拟合值之间离差平方和的平均值,其表达式为:
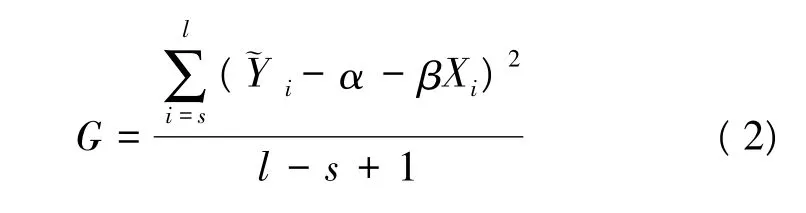
式中,α、β为离散点拟合直线方程Y=α+βX的系数,离散点i的观测点坐标记为(Xi,˜Yi),对应拟合直线上的坐标为(Xi,Yi),i=1,2,3,…,s…,l…,n(Xs,Ys)是第S个点,是拟合直线连续区间的起点;(Xl,Yl)是第l个点,是拟合直线连续区间的终点,且满足1≤s≤l≤n。当G具有最小目标值时,适应度值f即为最大值,此时所对应的连续区间[s,l] 就是无标度区间,即存在土地利用空间分形特征的尺度域。为了避免局部最优的假象出现,必须要求无标度区间是由一定数量的连续离散点组成;此时根据样本的个数,可以加入连续区间[s,l] 不小于某个固定常数作为约束条件,当搜索空间中某些点不符合上述约束条件时,则将其淘汰。
2.3 遗传算子设计
遗传算子包括选择、交叉和变异3种基本形式。在适应度函数的基础上进行选择算子的设计,本文采用轮盘赌模型,计算出连续区间内各个离散点所对应的适应度值,并求和得到该区间内全部点的适应度总值,此时适应度总值即为整个轮盘,最后依据离散点所占区间的比例来决定其被选择进入到下一代离散点连续区间群体中的概率[22]。对于交叉算子的设计,本文采用单断点交叉法,随机选择一个断点,交换双亲离散点区间中断点的右端,生成新的连续区间。应用该方法,交叉概率越大,代表交换的基因数越多,其值变化就越快,故迭代解算过程的收敛速度就越快。变异算子的设计则通过改变某些基因,使子代保持一定的遗传,又具有一定的进化,本文采用高斯变异算子进行变异,可以改善遗传算法的局部搜索能力,维持群体的多样性,并可防止出现早熟现象,特别适合土地利用在空间尺度采样上具有离散的特点。综合运用3种算子,通过返回适应度函数进行计算来判断是否满足优化标准,如此循环直到输出最优个体为止,即求得土地利用空间分形特征的尺度域。
2.4 半径维数
半径维数最初由Frankhauser等在1991年提出的,直到1993年White和Engelen才开始将其用于城市土地利用空间格局的分析中。当前,主要体现在用它来表达城市活动强度[23],本文选用半径维数来描述水域用地空间密度由城市中心到四周郊区的分布变化规律。
对于城市的某一类用地,假设以城市中心作为圆心,半径r范围内的该类型用地的面积为S(r),则S(r)的关系满足:

式中,η为常数,D为半径维数。半径维数D反映了该类用地的密度从城市中心向四周变化规律。由于该维数是根据“面积-半径”关系来定义的,所以它被称为半径维数[24-25]。
对公式(4)两边取自然对数,则将其化简为:
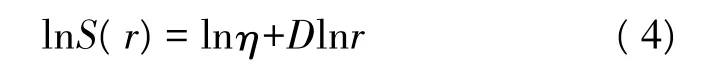
根据上述回归模型,只要测量出不同半径r范围的该类土地斑块的面积S(r),就可以利用最小二乘方法来求出半径维数D。本文以水域的半径维数计算为例,采用公式(4)来开展土地利用空间分形特征尺度域的识别研究。当D<2时,表示水体的空间分布从中心向四周逐渐衰减,呈非线性、不均匀变化,越往四周衰减速度越快;当D=2时,表示水体从中心向四周是均匀变化的;当D>2时,表明水体空间分布从中心向四周非线性逐渐增大。
3 结果与讨论
3.1 武昌区水域用地空间信息
以武昌区的边界重心作为几何中心、半径步长r为300 m来建立圆形缓冲区,利用ArcGIS的叠置分析来分割土地利用分类图,从中提取不同半径范围r中的水域面积S(r)。为了计算水域半径维数D,分别对半径和面积取自然对数,得到其双对数lnr和lnS(r),作为利用遗传算法求解土地利用空间分形特征尺度域的直接实验数据,见表1。当不考虑无标度区间存在时,可以根据表1中的数据和公式(4)计算水域的半径维数为3.006,测定系数为0.946,标准差为0.21。
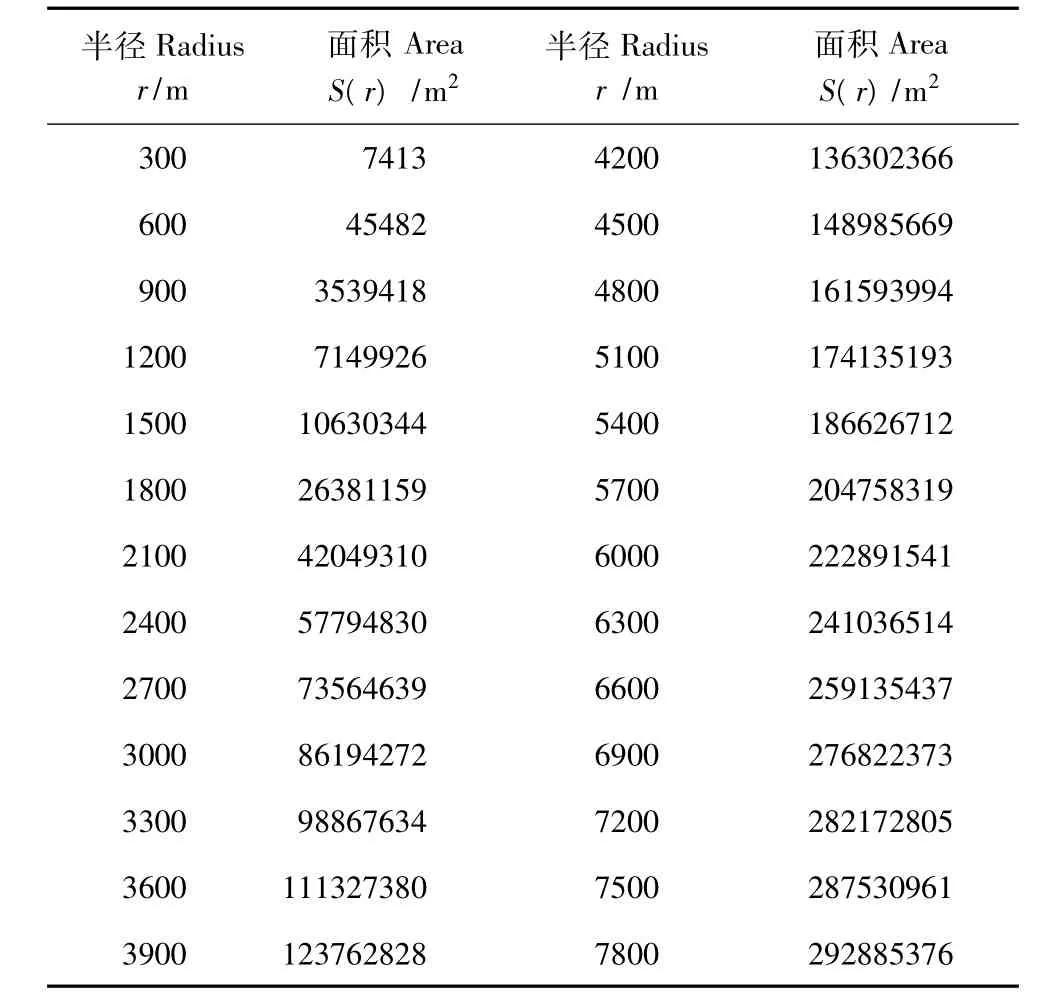
表1 武昌区不同半径r对应的水域用地面积S(r)Table1 The corresponding water areas r within different radiuses S(r)of Wuchang district
3.2 分形特征尺度域识别结果
在运用遗传算法识别水域半径维数的过程中,利用MATLAB7.0软件的遗传算法工具箱,选择尺度域约束条件为l-s≥5,变量个数设置为2,种群大小为26,初始范围设为[1,26] ,选择算子为轮盘赌算法,复制参数/交叉概率设为0.9,交叉算子设为单点交叉类型,变异算子选择高斯模型。根据公式(1)和(2)编制相应的适应度函数,加载表1中数据后,利用遗传算法工具箱对其进行调用,得到水域半径维数空间尺度的最优解,即为无标度区间。为了验证遗传算法识别土地利用空间分形特征尺度域的效果,本文选择人工判断法、相关系数法、强化系数法3种传统方法同遗传算法进行对比。4种方法识别尺度域的结果如表2所示。
3.3 结果分析与精度评定
针对4种方法识别分形特征尺度域的范围,本文采用最小二乘法对位于该范围内部的离散点进行线性拟合,计算得到水域的半径维数依次为1.375、2.118、1.310和1.285,如图4所示。它们同不考虑无标度区间所计算出来的半径维数(3.006)相比,在反映分形特征上均有较大的差别,甚至是截然相反的趋势。例如,图4中人工判断法、强化系数法及遗传算法计算得到的结果均小于2,说明武昌区水域空间分形特征从中心向四周都是非线性的减弱趋势,这同图2遥感影像解译出的水域空间分布信息是十分吻合的:武昌区的水域空间分布主要集中在中部的沙湖和东北部的东湖,从中心向四周发散的其它大部分方向都是减弱趋势的。但是,当没有考虑无标度区间存在情况下,如果直接利用其计算出来的半径维数去解释武昌区的水体空间分布格局,其趋势应该是从中心向四周其密度不断增大,这完全同水域实际空间分布相背离。因此,分形维数的计算应该要充分考虑无标度区间的存在,这对土地利用空间分形特征的研究十分必要。

表2 分形特征尺度域识别结果Table2 The results of scale domain recognition for fractal feature
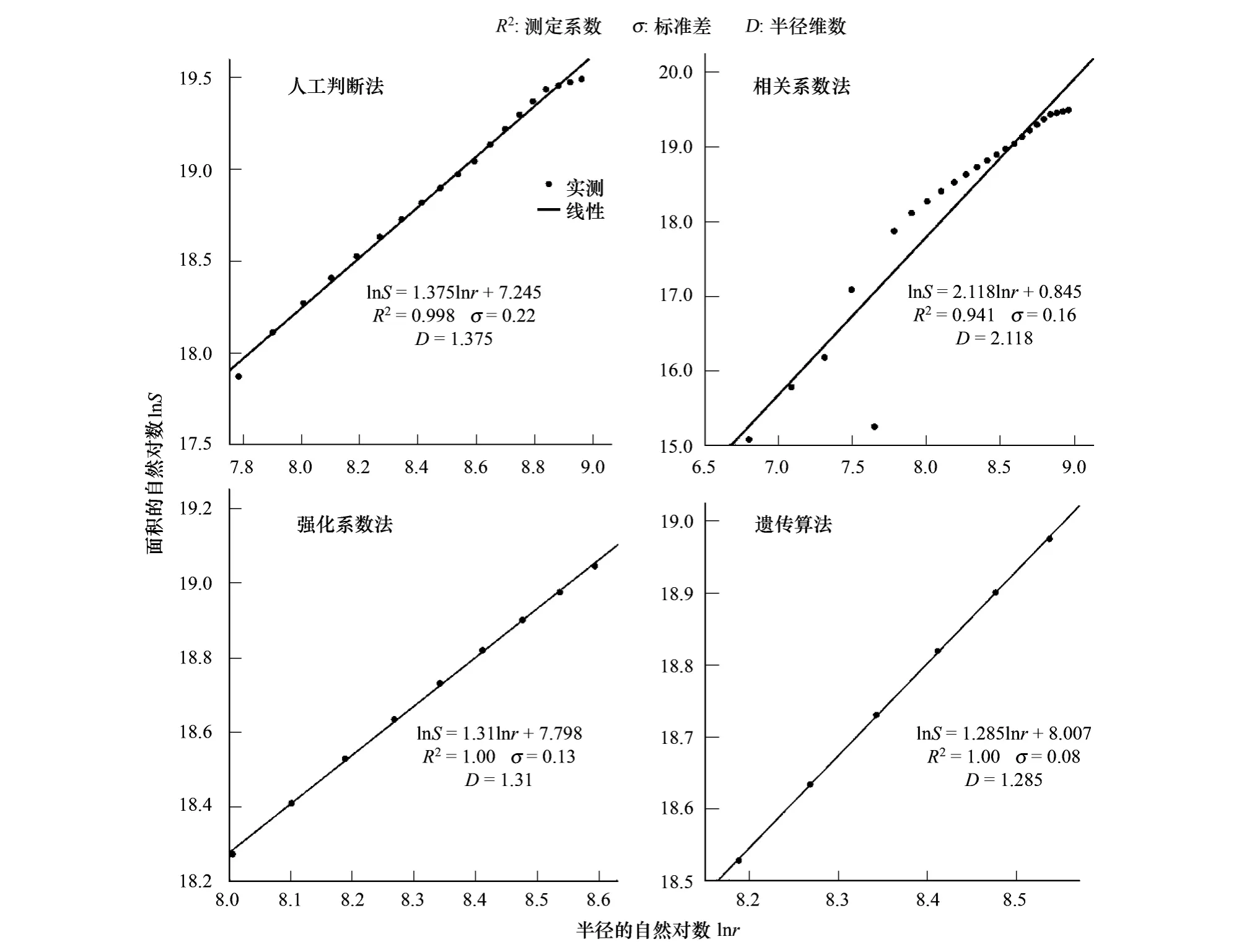
图4 四种方法无标度区间分形拟合结果Fig.4 The fitting results of scale-free region based on four methods
当然,采用不同方法去识别分形无标度区间范围也存在一定的差异,其对应分形维数拟合计算的结果也不尽相同,导致利用它们来评价水体空间密度的变化趋势也有较大出入。由表2和图4可以看出,相关系数法所得到的半径维数为2.118,相对于不考虑无标度区间所计算得到结果而言,二者的值都大于2;从半径维数的意义来看,它们表明武昌区的水域空间分布特征从中心向四周是非线性增加趋势,但这与实际情况是不相符合的,是错误的结果。另一方面,虽然人工判断法、强化系数法和遗传算法计算得到的结果均小于2,反映水域空间分布的趋势同实际情况相符合,但是其准确性也有一定差别。
为了进一步验证遗传算法相对于传统方法在分形无标度区间识别上的优势,根据测定系数和标准差等拟合指标来展开对比分析。从图4可以看出,遗传算法相对于其它3种算法来说,具有更好的分形无标度区间识别效果。其中,人工判断法较为简便而直观,在整体上比较准确,但局部精度不够。相关系数法在选择无标度区间上较人工判断法更为客观;但该方法是将双对数点图上所有可能的点对的组合(一般不小于3个点)进行线性相关系数检验,以置信度最高或线性范围最宽为标准来确定无标度区间。然而,采用取置信度最高为标准通常难以使其标准合理化,因为在数学上点数较少的组合在很大程度上对应着置信度最高的区间范围,这也就导致该方法常常会陷入局部最优的假象。在本文的对比实验中,采用一定置信度条件下线性区间范围最宽作为计算准则,其识别结果为[900,7800] ,基本上就等于整个实验区分析范围,得到的检验结果过于宽松,不能准确反映出分形无标度特征,这在识别离散点分布的弯曲性方面尤为明显;同时,该方法由于属于穷举法,存在着计算量过大和速度较慢的缺点。强化系数法相比于前面两种方法,其无标度区间较为准确,拟合效果好,结果也更客观。虽然它在一定程度上改进了相关系数检验法,可以有效解决无标度区间范围过宽的问题,但本质上仍是一种经验性方法,理论上不够严密,对离散点弯曲的分布(如Poisson分布)的识别能力仍不高。遗传算法在求取无标度区间时得到的标准差最小,拟合度的测定系数也最高,反映出遗传算法在精度上较其它方法具有优势。此外,由于采用非线性搜索策略,从而具有更高的效率,一般迭代在30次以内就可以达到最佳拟合度。因此,在土地利用空间分形特征的研究过程中,不仅要考虑到无标度区间的存在,而且要能够准确地识别其范围,才能确保土地利用空间分形特征研究的有效性。
4 结论与展望
本文以土地利用空间分形特征尺度域为研究对象,针对研究区水域这一典型土地利用类型,采用无标度区内离散点拟合的离差平方和平均值最小作为目标函数来设计适应度函数,提出了一种基于遗传算法的土地利用空间分形特征尺度域的识别方法,并将其结果同传统识别无标度区间方法的计算结果进行对比分析,主要得到以下结论:(1)当忽略无标度区间的存在,直接进行分形维数的计算时,所得到的分形维数并不能真实反映土地利用空间分形特征,此时分形维数将失去意义。因此,无标度区间的识别是计算分形维数的前提,它的存在对于开展土地利用空间分形特征的研究至关重要。(2)采用不同的方法所识别出的无标度区间不同,其所反映的分形特征也具有差异性。只有选择合适有效的方法才能精确地识别出无标度区间范围,有利于根据分形维数来合理解释土地利用空间格局的分形特征。(3)相对于传统人工判断法、相关系数法和强化系数法来说,遗传算法在识别分形尺度域上具有较大的优势。基于该算法识别出的无标度区间标准差最小、拟合度最高,所反映出来的分形特征与实际空间分布最吻合。
然而,分形维数的计算结果不仅同无标度区间大小有关,而且也与研究区域的范围有关[24],因此在今后的研究中需要进一步探讨多种因素对分形计算的影响。此外,采用不同遗传选择算子(随机遍历抽样法、期望值选择方法和锦标赛选择法等)来识别土地利用空间分形特征的尺度域,其效果也值得进行深入对比分析。
[1] Cheng L,Li F,Deng H F.Dynamics of land use and its ecosystem services in China's megacities.Acta Ecologica Sinica,2011,31(20):6194-6203.
[2] Zhu X H,Cai Y L.Fractal analysis of land use in China.Scientia Geographica Sinica,2005,25(6):671-677.
[3] White R,Engelen G.Cellular automata and fractal urban form:a cellular modelling approach to the evolution of urban land-use patterns.EnvironmentandPlanningA,1993,25(8):1175-1199.
[4] Batty M.Fractals-geometry between dimensions.New Scientist,1985,105(1405):31-35.
[5] Lam N S N.Description and measurement of Landsat TM images using fractals.Photogrammetric Engineering and Remote Sensing,1990,56(2):187-195.
[6] Torbick N M,Qi J G,Roloff G J,Stevenson R J.Investigating impacts of land-use and cover change on Wetlands in the Muskegon River Watershed,Michigan,USA.Wetlands,2006,26(4):1103-1113.
[7] Chen Y G,Luo J.A tentative theoretical interpretation of the fractal dimension of urban form.Urban Studies,2006,13(5):35-40.
[8] Deng L,Wu M,Ding S L.The research on land use types in Jinxi town by using fractal theory.Energy Environmental Protection,2012,26(6):14-16.
[9] Dang J W,Shi Y,Huang J G.The identification of fractal scaleless band in the study of fractal with computers.Computer Engineering and Applications,2003,39(12):25-27.
[10] Yokoya N,Yamamoto K,Funakubo N.Fractal-based analysis and interpolation of 3D natural surface shapes and their application to terrainmodeling.ComputerVision,Graphics,andImage Processing,1989,46(3):284-302.
[11] Gou X Q,Zhang Y J.The novel method of identifying the fractal scaleless range based on wavelet transform modulus maxima.Journal of Northwest Normal University:Natural Science,2005,41(5):28-30.
[12] Cai J H,Long Y,Wu H H,Chen D.Automatic determination of fractal non-scale interval of map objects based on inverse‘S’mathematical model.Geomatics and Information Science of Wuhan University,2004,29(3):249-253.
[13] Chen ZD.Theapplicayionofgeneticalgorithmtothe determination of fractal scale invariant region.Journal of Numerical Methods and Computer Applications,1996,(4):279-283.
[14] Fei B,Jiang Z D,Wang H R.Genetic algorithm for determining scale independent fractals associated with grinding surface.Journal of Xi'an Jiaotong Unvirsity,1998,32(7):72-75,84-84.
[15] Wu Z C.Determination of fractal scaleless range.Acta Geodaetica Et Cartographica Sinica,2002,31(3):240-244.
[16] Fan Y H.Fractal Terra in Generation and Fractal Dimension Evolution Analysis of Subsidence[D] .Qingdao:Shandong University of Science and Technology,2005.
[17] Zheng H M.On function to the city from urban lake.Journal of Nanping Teachers College,2007,26(2):132-135.
[18] SEPA(State Environmental Protection Administration).The Notification About the Present Situation Survey of the Ecological Environment in Central and Eastern Regions.(2002-04-11)[2013-11-13] .http://www.zhb.gov.cn/gkml/zj/wj/200910/t20091022_172095.htm.
[19] Wang X P,Cao L M.Application and Software Implementation of Genetic Algorithm.Xi'an:Xi'an Jiaotong University Press,2002:7-14.
[20] Chen G L,Wang X F,Zhuang Z Q,Wang D S.Genetic AlgorithmandItsApplication.Beijing:Posts&Telecommunications Press,1996:3-12.
[21] Michalewicz Z.Genetic Algorithm+Data Structures=Evolution Programs.New York:Springer,1992:5-30.
[22] Guo J,Chen Q W,Zhang X Q,Li W F.Optimization of lake model salmo based on real-coded genetic algorithm.Acta Ecologica Sinica,2012,32(24):7940-7947.
[23] Chen Y G,Huang K.The fractal dimension of urban form:theoretical approach and practical significance.Journal of Xinyang Teachers College:Natural Science Edition,2002,15(1):62-67.
[24] Jiang S G,Zhou Y X.The fractal urban form of Beijing and its practical significance.Geographical Research,2006,25(2):204-212.
[25] Bai X P.Spatial pattern change research of land use based on fractal dimensions in Tianjin new coastal area.Journal of Anhui AgriculturalSciences,2011,39(24):14728-14730,14808-14808.
参考文献:
[1] 程琳,李锋,邓华锋.中国超大城市土地利用状况及其生态系统服务动态演变.生态学报,2011,31(20):6194-6203.
[2] 朱晓华,蔡运龙.中国土地利用空间分形结构及其机制.地理科学,2005,25(6):671-677.
[7] 陈彦光,罗静.城市形态的分维变化特征及其对城市规划的启示.城市发展研究,2006,13(5):35-40.
[8] 邓林,吴敏,丁桑岚.基于分形理论的土地利用空间格局分析——以金溪镇为例.能源环境保护,2012,26(6):14-16.
[9] 党建武,施怡,黄建国.分形研究中无标度区的计算机识别.计算机工程与应用,2003,39(12):25-27.
[11] 苟学强,张义军.分形无标度区的小波变换模极大识别.西北师范大学学报:自然科学版,2005,41(5):28-30.
[12] 蔡金华,龙毅,毋河海,陈丹.基于反S数学模型的地图目标分形无标度区自动确定.武汉大学学报:信息科学版,2004,29(3):249-253.
[13] 陈遵德.遗传算法在自动确定分形标度不变区中的应用.数值计算与计算机应用,1996(4):279-283.
[14] 费斌,蒋庄德,王海容.基于遗传算法求解分形无标度区的方法.西安交通大学学报,1998,32(7):72-75,84-84.
[15] 巫兆聪.分形分析中的无标度区确定问题.测绘学报,2002(31):240-244.
[16] 范玉红.塌陷区分形地形生成和分维演变分析[D] .青岛:山东科技大学,2005.
[17] 郑华敏.论城市湖泊对城市的作用.南平师专学报,2007(26):132-135.
[18] 国家环境保护总局.关于开展中东部地区生态环境现状调查的通知.(2002-04-11)[2013-11-13] .http://www.zhb.gov.cn/gkml/zj/wj/200910/t20091022_172095.htm.
[19] 王小平,曹立明.遗传算法——理论、应用与软件实现.西安:西安交通大学出版社,2002:7-14.
[20] 陈国良,王煦法,庄镇泉,王东生.遗传算法及其应用.人民邮电出版社,1996:3-12.
[22] 郭静,陈求稳,张晓晴,李伟峰.基于实码遗传算法的湖泊水质模型参数优化.生态学报,2012(32):7940-7947.
[23] 陈彦光,黄昆.城市形态的分形维数:理论探讨与实践教益.信阳师范学院学报:自然科学版,2002,15(1):62-67.
[24] 姜世国,周一星.北京城市形态的分形集聚特征及其实践意义.地理研究,2006,25(2):204-212.
[25] 白新萍.基于分形理论的滨海新区土地利用空间格局变化研究.安徽农业科学,2011,39(24):14728-14730,14808-14808.
