基于FPGA的IIR数字滤波器的设计及测试分析

2014-08-03魏运锋谈卿瑕赵晓丹

化工自动化及仪表 2014年7期

韩建魏运锋谈卿瑕赵晓丹

(1.东北石油大学电子科学学院，黑龙江大庆 163318；2.大庆油田公司，黑龙江大庆 163318)

数字滤波器主要有无限冲激响应数字滤波器(Infinite Impulse Response Digital Filter，IIR数字滤波器)和有限冲激响应数字滤波器(Finite Impulse Response Digital Filter，FIR数字滤波器)[1]。与FIR数字滤波器相比，要实现同样的衰减特性，IIR数字滤波器的阶数比FIR滤波器要低，通常也消耗较少的硬件资源，对于不要求线性相位的场合，IIR滤波器则更为适合[2]。

笔者采用FPGA技术，应用硬件描述语言实现IIR数字滤波器的设计。基于其串联网络结构的特点，先实现低阶数字滤波器，再串联实现高阶数字滤波器。根据设计的数字滤波器系数，结合研究算法，在Quartus II软件环境下，对程序进行了仿真，仿真结果初步说明了算法程序的有效性。

1 IIR滤波器的算法实现①

实现高阶的IIR数字滤波器，可通过实现低阶的IIR数字滤波器，然后串联得到高阶IIR数字滤波器的方法。笔者设计是六阶IIR数字滤波器，要实现该滤波器，可根据系数先实现二阶IIR数字滤波器[3]。一个二阶的IIR滤波器的系统函数如下：

为了编程方便，把a0化为1，并且采用二阶IIR滤波器的转置网络结构，如图1所示。

图1 二阶IIR滤波器的转置网络结构

1.1 数制的规定

笔者实现IIR数字滤波器采用定点数制。为了避免计算中数据溢出和数据截短造成的计算错误，对数据的表示和处理进行了如下规定。

输入和输出数据用17位定点数表示，最高位为符号位，最后4位为小数部分，中间的12位为整数部分[4]。

系数用14位定点数来表示，由于最小量化单位为1/4096，定点数的格式是最高位为符号位，接下来一位为整数位，剩下的12位为小数位，该格式可以表示的数的范围是-2～2。

运算过程中需要将系数和数据相乘，两个不同格式定点数相乘会发生小数点移位。因此运算过程中的数据用30位定点数表示，格式为最高位为符号位，接下来的13位为整数位，剩下16位为小数位。

反馈数据与输入、输出数据格式相同。反馈数据是通过运算过程中的数据截短而来的，反馈数据取运算中间数据的符号位和第28位到13位组成[5]。如需实现其他指标的数字滤波器，数量表示可以灵活调整。

1.2 滤波器的电路结构

IIR滤波器由有符号乘法器、延时器和加法器组成，其电路结构如图2所示。

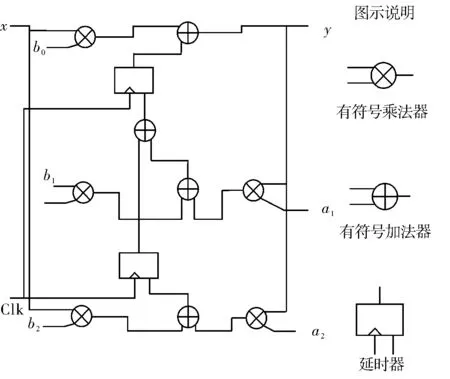
图2 IIR滤波器的硬件结构

有符号乘法器。有符号乘法器乘数必须为原码，且由3个部分组成。首先是无符号的乘法器，用于计算输入乘数除开符号位的部分的乘积。第二部分是将两个乘数的符号位异或，得到输出数的符号位。最后一个部分是把前两部分的输出合

并转换为补码[6]。根据数制规定，图中的5个乘法器输入数据分别为述的17位和14位定点数，输出为30位定点数。

有符号加法器。有符号加法器的两个加数都为补码。这些加法器的输入、输出均为30位。

延时器。延时器是30位的上升沿D触发器。

2 六阶IIR数字滤波器的实现

实现六阶IIR数字滤波器，可将3个二阶滤波器串联在一起。但是两个二阶滤波器之间要接一个转换器。文中模拟信号量化数据均为8位，所以在处理前，先把这些数据转换为规定的17位定点数。由于二阶IIR滤波器的输入、输出均为17位定点数补码，而有符号乘法器要对源码进行运算，因此两个二阶滤波器用一转换器连接，其作用是将补码转换为源码，以便下个滤波器的乘法器使用。另外一方面，处理结束后，送入D/A的数据只能有8位，所以在最后一个二阶滤波器的输出数据须转换为8位[7]。六阶IIR滤波器的实现如图3所示。

图3 六阶IIR滤波器的实现框图

3 IIR滤波器的测试分析

根据FDAtool所设计的IIR数字滤波器系数，用Verilog HDL结合算法编写数字滤波器IIR程序。以下是对实现的IIR滤波器的仿真，输入是正弦信号，频率分别100、200、2 000、4 000、5 000Hz。IIR滤波器指标为六阶Butterworth带通滤波器，采样频率为44 100Hz，下截止频率为200Hz，上截止频率为4 000Hz。仿真结果如图4所示。

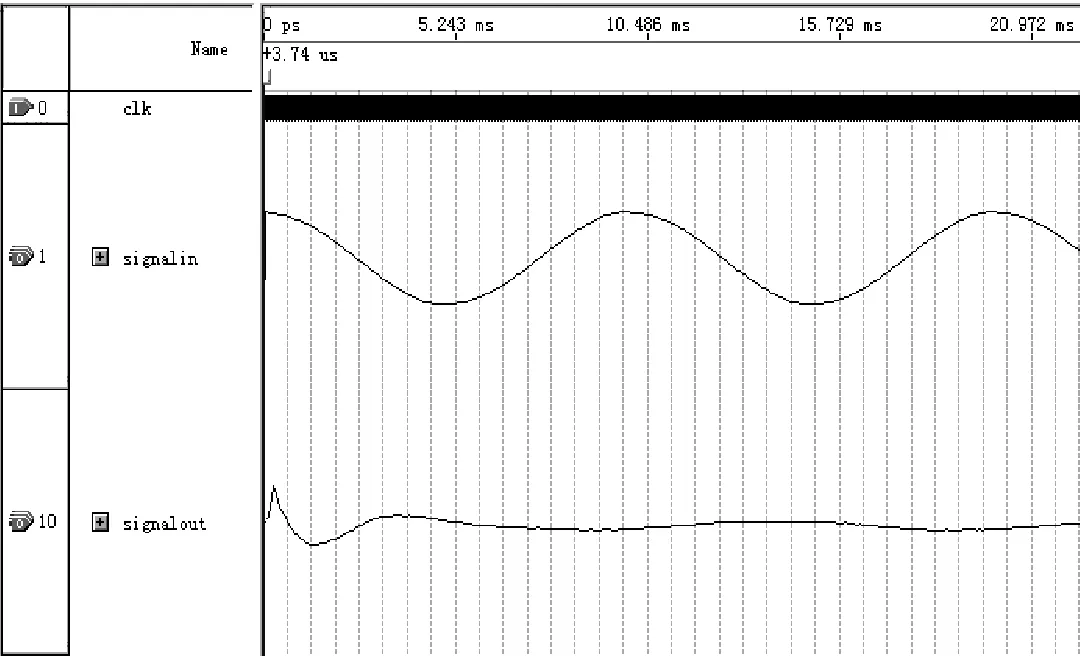
a. f=100Hz

b. f=200Hz

c. f=2000Hz

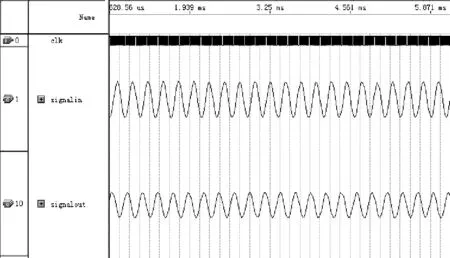
d. f=4000Hz

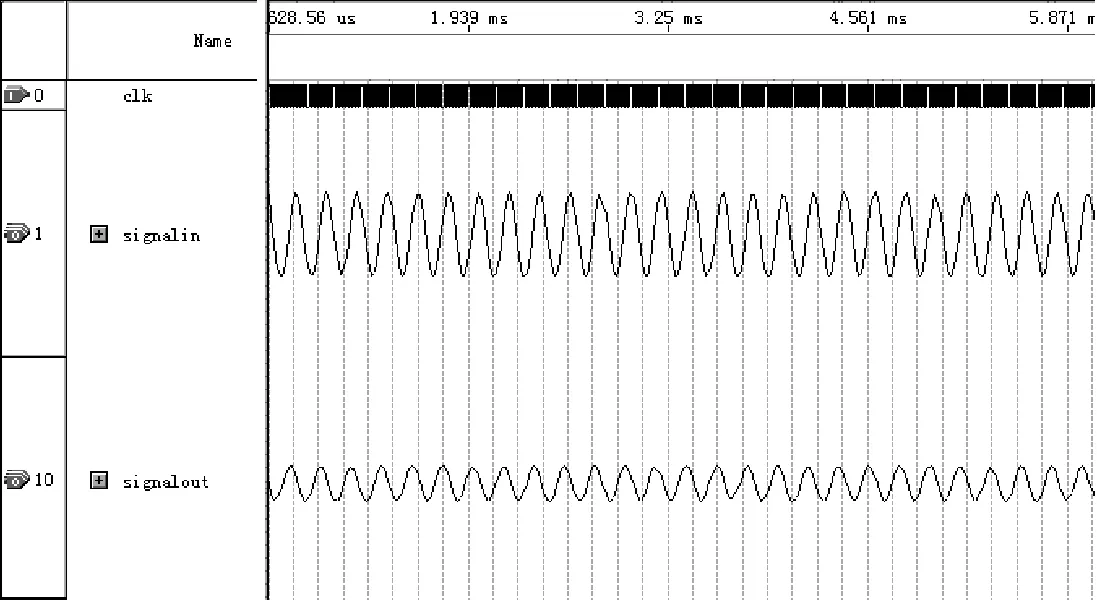
e. f=5000Hz

图4中，输入和输出波形均符合正弦函数。输入正弦频率为100Hz和5 000Hz时，输出波形均有明显的衰减，输入正弦频率为200Hz和4 000Hz时，输出波形有轻微衰减，输入正弦频率为2 000Hz时基本无衰减，这说明滤波器已经显现出了带通特性。表1列出了滤波器输入、输出波形的幅度和衰减与FDAtool所设计出的理论值的比较。