各向异性木材的热传导

林 铭, 饶久平, 谢拥群, 杨庆贤, 廖益强

(福建农林大学材料工程学院，福建 福州 350002)

各向异性木材的热传导

林 铭, 饶久平, 谢拥群, 杨庆贤, 廖益强

(福建农林大学材料工程学院，福建 福州 350002)

在对空间变量进行变换的基础上，引入木材等效导热系数及其与弦向、径向、顺纹3个主导热系数之间的数量关系，简化了各向异性木材中热传导的非稳态偏微分方程;再应用数学物理方法求解各向异性木材传热过程中温度场时空分布的解析解.

木材; 各向异性; 热传导; 温度场; 解析解

木材是一种典型的天然多孔性材料.多孔性材料一般具有非均匀性和各向异性的物理特征，而这2种物理特征使得木材热传导问题的研究复杂而困难[1-4].木材是一种非晶体的各向异性物质.各向异性物质的导热系数一般包含9个分量，是一个二阶张量.因此，不能简单地应用傅里叶(Fourier)热传导定律来描述木材中的热流密度.木材热传导偏微分方程中出现空间变量的交叉导数使得分析各向异性木材中的热传导变得极其复杂.目前这方面的研究主要有应用有限元法计算木材中温度场的数值解[5-7]，以及给出温度场的一个形式解[8-10].

在木材的干燥、防腐、改性等各种热处理加工及各种实际应用中，若能给出各向异性木材热传导的温度场分布及其随时间变化的解析函数，则可准确计算木材内部各点的温度梯度及其随时间的变化，有助于定量分析木材受热时内部各点的热应力、应变情况.有关各向异性木材中热传导的非稳态偏微分方程解析解的研究尚未见报道.本文应用数学物理方法求解各向异性木材中热传导的非稳态偏微分方程的解析解.

1 各向异性木材中的热流密度

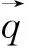
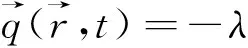
(1)

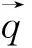
(2)

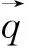
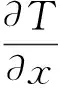
(3)

但是，在诸如木材这样的各向异性介质中，导热系数不是一个恒量，而是一个二阶张量

(4)

即导热系数包含9个分量λij,i,j=1,2,3.于是热流密度在直角坐标系中沿3个坐标轴的分量是沿3个坐标轴方向的温度梯度的线性组合，即

(5)

根据不可逆过程热力学的昂赛格(Onsager)原理，式(5)中的唯象系数服从互易关系，即

λij=λjii,j=1,2,3

(6)

而且系数λij(i≠j)存在下列关系

(7)

2 各向异性木材中热传导的偏微分方程

根据能量守恒定律，在单位时间内通过木材中任一闭合曲面S流进的净热量等于该闭合曲面S所围的体积V内能量的增量，即

(8)

式中负号表示取曲面的外法线方向为正，ρ和c分别为木材的密度和比热.

按照高斯定理，对于空间的任意区域V(S为区域V的界面)有

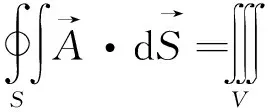
(9)

(10)

把式(5)代入式(10)，整理后得

(11)

根据昂赛格互易关系，式(11)中的系数存在如下关系：

λ12=λ21λ13=λ31λ23=λ32

(12)

由于各向异性木材的非稳态偏微分方程(式(11))中包含有空间变量的交叉导数，使得求解该微分方程变得十分复杂.利用木材的各向异性所具有的正交性，可简化该微分方程.取木材3个相互垂直的径向、弦向和顺纹方向作为主轴，相应的主导热系数分别记作λr、λt、λa.以这3个主轴建立正交坐标系，则可把式(11)简化为

(13)

作空间变量变换，令

(14)

式中λeqv称为等效导热系数.

把式(14)代入式(13)，则

(15)

根据式(14)，原空间的体积元dxdydz可变换成

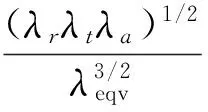
(16)

为了使式(16)中与空间有关的物理量在空间变换前后具有相同的空间意义，须令

(17)

根据式(17)，可得等效导热系数与木材3个主导热系数间的关系

λeqv=(λrλtλa)1/3

(18)

3 各向异性木材中温度场时空分布函数

设热处理的木材长度L远大于其半径R，初始(时间t=0)温度为T0，热处理温度为T1.考虑到热处理木材的界面是圆柱面，坐标系的选择应以木材中心轴为z轴，建立柱坐标系(r, Ø,z).

在柱坐标系中，偏微分方程(式(15))表示为

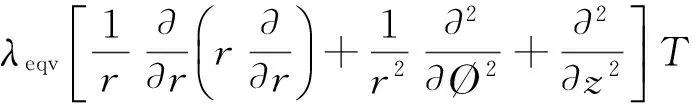
(19)

由于木材内部的温度场是对z轴对称分布的，因此温度T与变量Ø和z无关，仅是r和t的函数.这时式(19)可简化为

(20)

式(20)的边界条件和初始条件分别为

(21)

(22)

对非齐次的边界条件式(21)进行齐次化处理，令

T(r,t)=A(r,t)+T1

(23)

把式(23)分别代入式(20)-(22)，得到微分方程的定解：

(24)

设变量A可分离成以下形式

A(r,t)=B(r)H(t)

(25)

把式(25)代入式(24)中的第1式，得到关于B(r)和H(t)的2个常微分方程

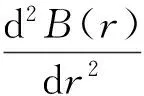
(26)

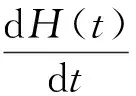
(27)

式中k2是分离变量常数.

方程(26)是零阶贝塞尔(Bessel)方程，在r=0处的有界解是

B(r)=J0(kr)

(28)

要使这个解满足式(24)中的第2式，则

B(R)=J0(kR)=0

(29)

则kR必须等于零阶贝塞尔函数J0的零点μn，n=1,2,….其本征值

kn=μn/R

(30)

相应的本征函数为

Bn(r)=J0(μnr/R)

(31)

式中0<μ1<μ2<….

把式(30)代入式(27)，易得该含t常微分方程的解为

(32)

把式(31)、(32)同时代入式(25)，得到A(r,t)解的一般形式

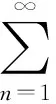
(33)

将式(33)代入式(24)中的第3式，得

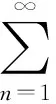
(34)

把式(34)右边的T0-T1在[0,r]区间上展开为傅里叶-贝塞尔(零阶)级数，即

(35)

(36)

通过比较式(34)和式(35)，可得Cn=Cm，对式(36)中分子进行积分，对其分母进行微分后，得

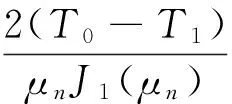
(37)

由式(23)、(33)和(37)得到各向异性木材中温度场时空分布函数T(r,t).

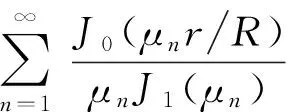
(38)

式中J0和J1分别是零阶和一阶贝塞尔函数，μn是零阶贝塞尔函数的第n个根，其数值均可以从相关数学手册中查到.当木材的径向导热系数λr、弦向导热系数λt、顺纹导热系数λa以及木材的横截面半径R、初始温度T0、干燥室温度T1为已知时，可以从式(38)和式(18)求出木材干燥过程任一时刻t、木材中任一点r的温度.

4 小结

(1)各向同性介质中，热流密度矢量方向与温度梯度方向一致，垂直于等温面.而诸如木材等各向异性介质中，热流密度矢量方向不一定垂直于通过考察点的等温面.

(2)各向异性木材中的热传导问题远比各向同性材料复杂.本文在对空间进行变换的基础上，引入等效导热系数，简化了木材中热传导偏微分方程.

(3)当木材热处理温度T1、木材初温T0以及木材半径R一经确定，便可通过式(38)计算出热处理过程中木材内部任一点的温度值及其随时间的变化趋势.

[1] 林铭,饶久平,谢拥群,等.木材径向导温系数数学模型[J].福建农林大学学报:自然科学版,2012,41(3):320-322.

[2] 杨庆贤.木材干燥过程中热质迁移交互作用的研究[J].福建林学院学报,1999,19(2):101-104.

[3] 杨庆贤,杨武,潘玉英,等.不可逆热力学研究木材干燥规律[J].山东科技大学学报,2003,22(2):105-106.

[4] 谢拥群,陈瑞英,杨庆贤，等.木材干燥过程的热质迁移及其耦合关系[J].林业科学,2004,40(1):148-153.

[5] 蔡力平,刘一星,尙德库.用有限元法分析木材中的温度分布[J].林业科学,1992,28(1):90-93.

[6] 郑世强,曹军.基于有限元理论木材温度场的数值仿真[J].森林工程,2007,23(1):11-14.

[7] 李文深,戴澄月,高瑞堂,等.木材热传导问题的研究[J].东北林业大学学报,1987,15(4):56-65.

[8] 高瑞堂,刘一星,李文深,等.木材热学性质与温度关系的研究[J] 东北林业大学学报,1985,13(4):22-26.

[9] [美]杰姆斯.传热学(上册)[M].俞佑平，译.北京:人民教育出版社,1980:44.

[10] [德]卡姆克.常微分方程[M].张鸿林，译.北京:科学出版社,1977:475.

(责任编辑:叶济蓉)

Heat transfer in anisotropic wood

LIN Ming, RAO Jiu-ping, XIE Yong-qun, YANG Qing-xian, LIAO Yi-qiang

(College of Material Engineering, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002, China)

The time-dependent partial differential equation of the heat transfer in anisotropic wood was simplified when a equivalent thermal conductivity of wood was introduced and the quantity relation between equivalent thermal conductivity and three principal conductivity of anisotropic wood was set up on the basis of space variable transformations. The analytic function of the temperature field from heat transfer in anisotropic wood was solved by means of the methods of mathematical physics.

wood; anisotropy; heat conduction; temperature field; analytic solution

2013-12-02

2014-05-21

国家自然科学基金资助项目(30271057).

林铭(1963-)，男，副教授，博士研究生.研究方向：木材科学与技术.通讯作者谢拥群(1960-)，男，教授，博士生导师.研究方向：植物纤维缓冲材料的性能.Email:fjxieyq@hotmail.com.

S781.37

A

1671-5470(2014)06-0657-04