基于数理统计的高精度CO2传感器校正方法

侯 明 张天仪 王 洁 张 健

(北京信息科技大学 a.自动化学院；b.理学院；c.经管学院，北京 100192)

CO2排放监测对于控制和改善全球温室气体效应有重要意义。在研究一种火电厂CO2排放计量系统时，需要检测一个内径较大气道内的CO2浓度，以计算其排放量。在气道内安置了多个采样吸嘴构成阵列以提高计量精度。单个传感器的浓度测量值是基本测量数据，其精度直接影响计量准确度。本项目中应用了一种新型超低功耗CO2传感器，需要对传感器进行实证测试，验证其精度，并进行校准。在大量的传感器校准过程中，希望能够根据较少的采样点得出理想的曲线[1]，以节省时间、提高效率。笔者就插值节点的选取进行了研究，为了获得更高的精度，尝试使用Kalman滤波与统计分布相结合的方法，并通过实验验证了该方法的有效性。

1 CO2浓度采样装置和数据采集方法①

在气体混合检测系统(图1)中通入不同流速比的空气与CO2，可得出不同的CO2体积百分比，用标准仪测量气缸中的百分比浓度。将数字传感器节点置于气缸中，通过串口将数据传至PC机的Matlab监控端，并把读取的数据进行存储与分析。在检测范围内(0%～100%)按增量方式调节流量计为15种开度，其精确浓度由校准仪表测得。气缸内CO2浓度稳定后，传感器节点采样2 000个点进行后续分析。

采样浓度因手动流量计的精度所限，不能保证等间隔，每次设定都存在一定的随机性，表1列出一次实验中的浓度值，并以此做校正。

图1 气体混合检测系统

表1 一次实验采集的CO2浓度 %

当标准仪表稳定在50.3%时以Z作为一组数据，通过对Z进行卡尔曼滤波处理得到另外一组数据[2]。在后续的曲线拟合中会对两种方式取得的采样值分别进行拟合，以对比拟合效果，同时说明期望值作为插值节点更能逼近理想曲线。

当气体浓度稳定时，把气缸看成一个系统，构建Kalman滤波方程：

X(k|k-1)=AX(k-1|k-1)+BU(k)

(1)

P(k|k-1)=AP(k-1|k-1)A′+Q

(2)

X(k|k)=X(k|k-1)+Kg(k)[Z(k)-HX(k|k-

1)]

(3)

Kg(k)=P(k|k-1)H′/[HP(k|k-1)H′+R]

(4)

P(k|k)=[I-Kg(k)H]P(k|k-1)

(5)

由于稳态过程中V%|k1=V%|k2，状态变量只有一个，所以选取状态系数A=1。由于气缸内没有气体交换，所以U(k)=0。由于协方差的初始值会影响系统的收敛性，这里P(0|0)=5。由于传感器的输出即浓度，所以状态方程的参数H=1。Q与R矩阵要依据具体的实验环境来测量获得。由于在数据采集时为气体的稳态值，环境相对稳定，没有诸如突然增加或减少气体浓度的情况，这里用方差较小的随机数替代。通过对采集的数据进行处理，得到的数据融合结果如图2所示。通过分析两组数据的概率分布特征和平滑效果可以看出，经过卡尔曼滤波后的数据效果更好。

图2 卡尔曼滤波前、后稳态数据曲线

2 求取插值节点

采样过程中的各种干扰、误差是不可避免的。如何从含有随机误差的实验数据中确定出最可靠的测量结果，并用概率分布描述测量和误差，在近代物理实验中显得非常重要。工程上常用的方法是多次采样求取平均值。平均值是统计学中最常用的统计量，为集中趋势最常用的测度值，目的是确定一组数据的均衡点。但是平均数也有不足之处，正是因为它利用了所有数据的信息，平均数容易受极端数据的影响，所以有时这种方式是不尽科学的，给数据的可靠性带来问题[3]。

在概率论和统计学中，期望值是随机变量的数字特征之一。一个离散性随机变量的期望值是实验中每次可能结果的概率乘以其结果的总和，定义如下：

f(υk)=P(X=υk)，k=0,1,2,…
E(X)≡∑kυkf(υk)

(6)

期望值是随机实验在同样的机会下重复多次的结果计算出的等同“期望”的平均值。可见，用期望值去近似采样时刻的真实值更为科学[4]。

鉴于数学期望更优的统计特性，在本实验中，以30.7%、50.3%浓度下采集的数据为例进行统计分析，样本记为X1、X2，其分布如图3所示。

图3 两个样本的稳态值分布

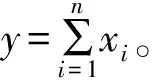
p(B)=1.43e-4

对于样本X1,数学期望和均值分别为：

E(X1)=n·p=28.59%

对于样本X2,同理求得数学期望和均值：

E(X2)=52.21%

现分别以数学期望和均值进行插值处理与精度验证。

3 插值拟合

插值拟合是数值分析领域的重要环节。工程中常用的拟合方法有理论直线法、端点直线法、最佳直线法和最小二乘法。而近代拟合曲线的方法常用的有模拟退火算法、遗传算法及蚁群优化算法等[6]。综合考虑算法的复杂度与操作的方便性，3次样条插值具有良好的收敛性与稳定性，实际应用中选用该方法进行插值[7]。由于传感器的分辨率为0.01，笔者选择插值步长为0.005。共对传感器采集了15个稳态值，由于传感器数据帧的特点，浓度值为100%的数据参考价值不大。但是根据算法要求，拟合时仍用了15个数据。分别对14个稳态值进行概率分布与求解期望值的处理，得出各个稳态值的期望。进行3次样条插值后的结果如图4所示。

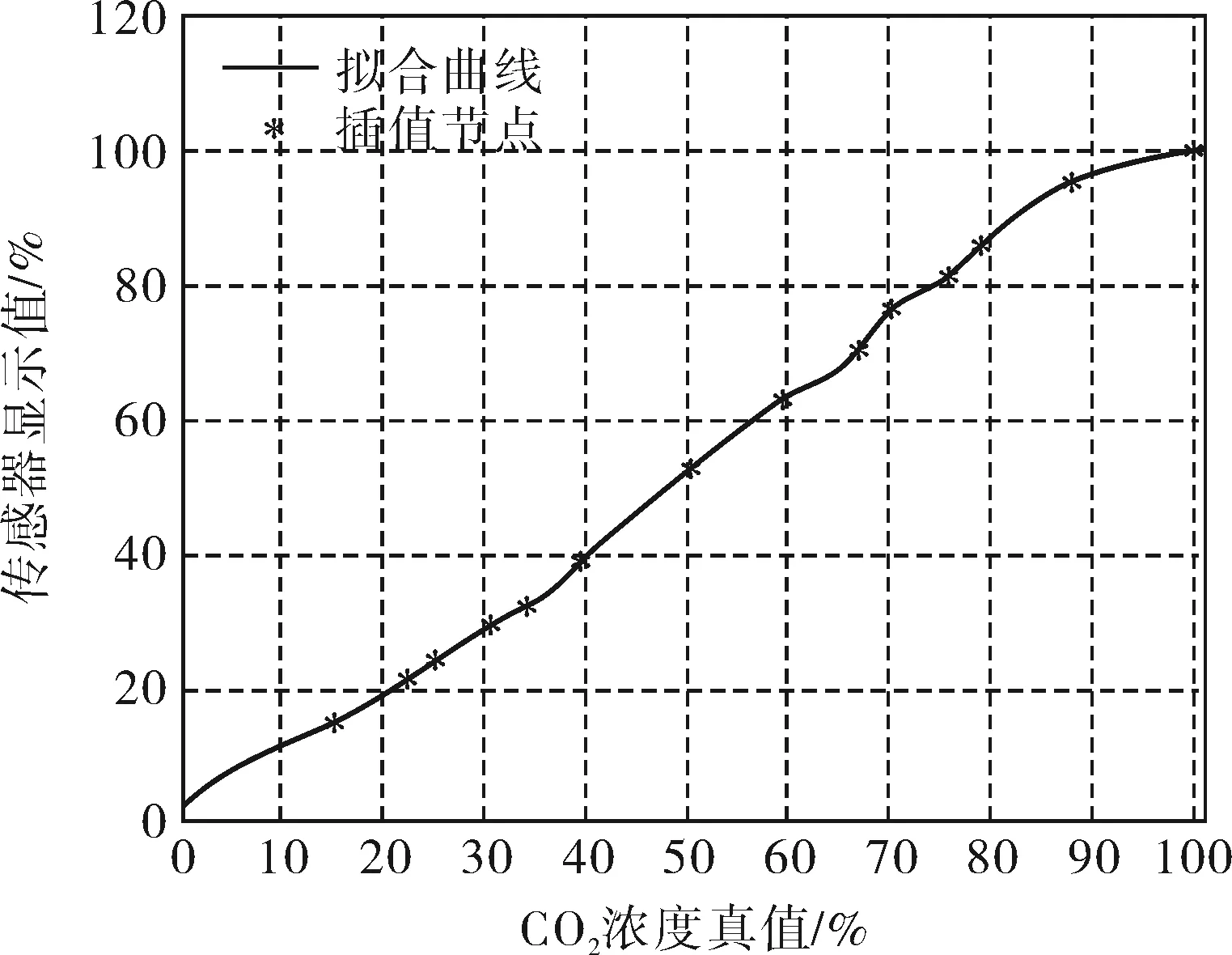
图4 3次样条拟合结果

4 验证分析

由于气体浓度受气温及气压等因素的影响，为了排除这些因素的影响，在分析验证时采用了这样一种方法：如果条件A={A1,A2,A3,A4,A5}是构成事件S的充分必要条件，条件A又受条件B(t)={B1(t),B2(t),B3(t),B4(t)}影响。现在构造一种条件A到S的映射关系f(x)，为了检验f(x)的可靠性，在较短时间内得到条件A，利用条件A与其中任一个条件Ak的差集通过f(x)构造出新的事件S′，利用f(x)求出类Ak的条件Ak′；通过比较S与S′的相似度或者条件Ak′与Ak的相似度来判定f(x)的可靠性。

本项目采取后者，具体来说就是把15个点的一个值xk抽掉，剩下的14个点进行插值拟合，选用Δxk=|xk-xsplinek|值的大小作为相似度的评判依据。通过分析Δx的特点，判定该方法的可行性，即求期望值作为插值节点的方法能否更好地计算出插值节点进而得到逼近实际的曲线。分别抽取了xk1=22.7和xk2=70.2，拟合效果如图5、6所示。

图5 浓度为22.7%时拟合结果对比

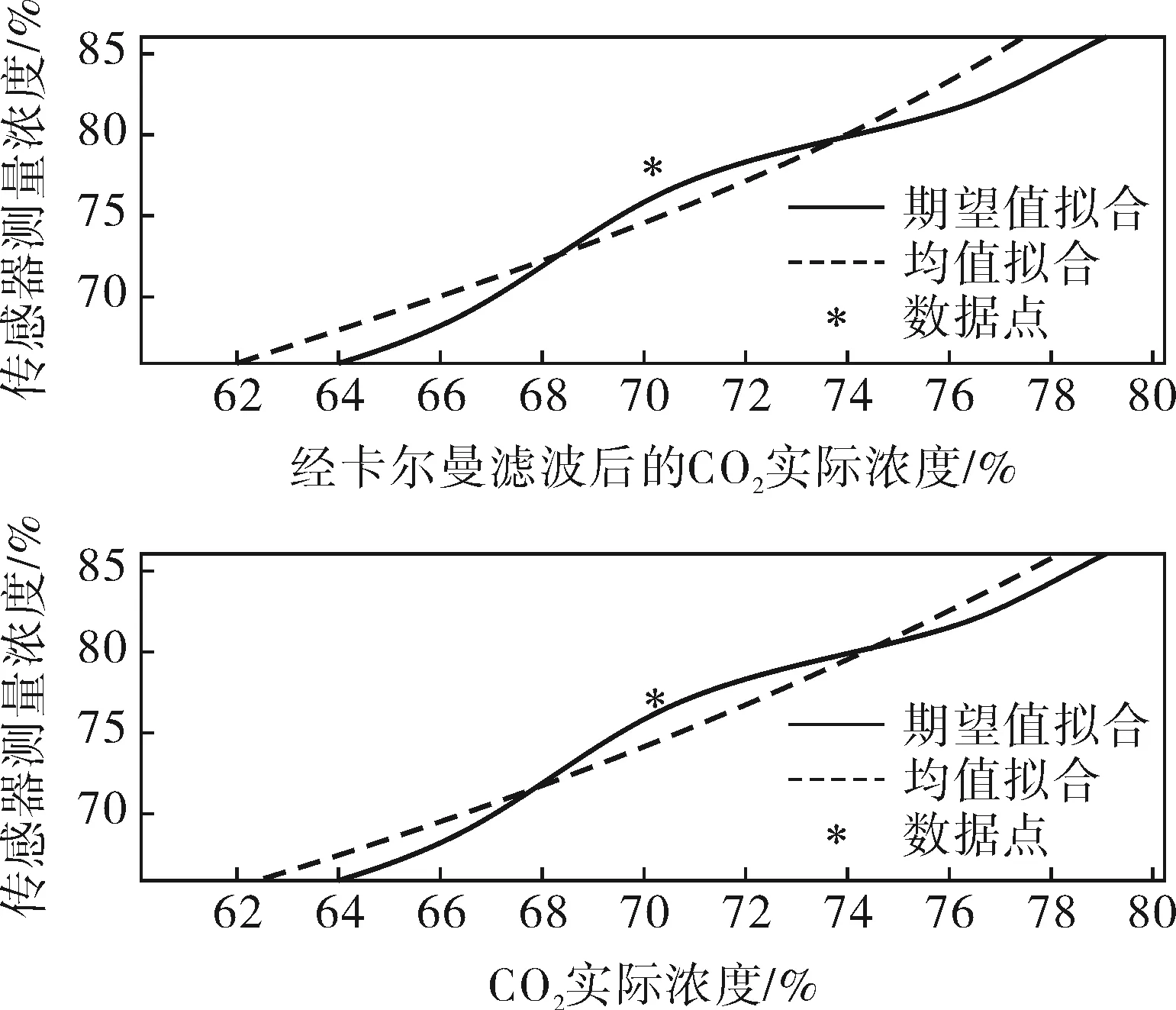
图6 浓度为70.2%时拟合结果对比

Δxk|k1经过滤波前、后的值分别为x1k1=0.78、x2k1=0.78。Δxk|k2经过滤波前、后的值分别为x1k2=0.66、x2k2=0.56。另外，为了研究采样间距对拟合效果的影响，选择D=|xk+1-xk-1|分别对14个值逐个抽取，得到的结果汇总于表2。

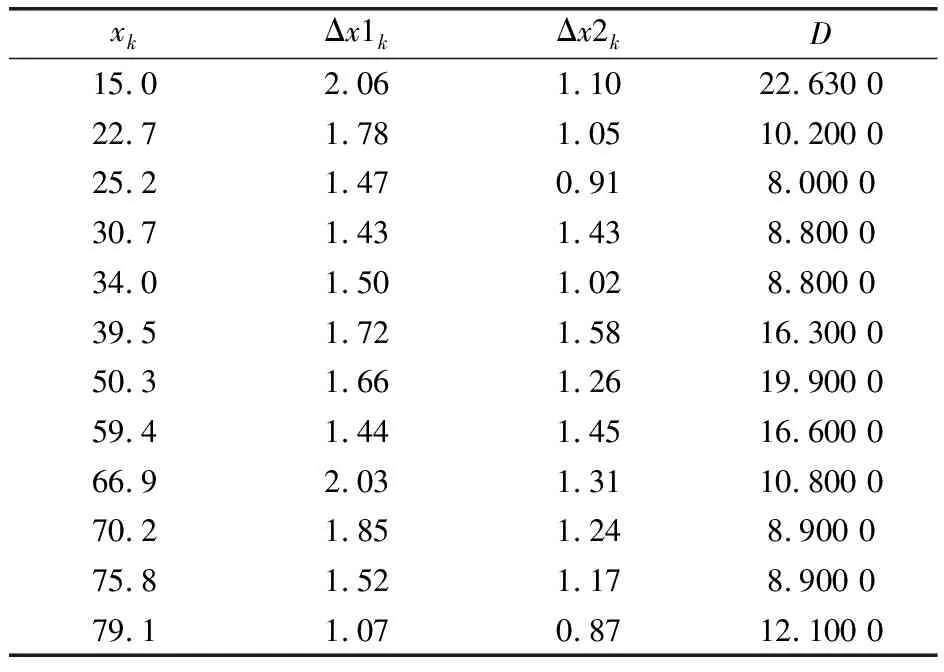
表2 误差分析

图7给出了均值拟合和期望拟合的误差。

图7 两种方式拟合误差结果

比较分析表2和图7得到以下结论：通过求采样点的数学期望可以更精确地得出传感器的插值结果。同比情况下经过卡尔曼滤波的采样数据能更好地得出拟合曲线；实践中获得的误差平均减小了13%。

5 结束语

在高精度校准曲线绘制要求的情况下，以概率分析稳态采样点的数据规律，能更好地估计出传感器的可信输出，进而计算出可靠的插值节点，从而获得更接近真实值的传感器特性曲线。笔者结合Kalman滤波和概率论统计的方法，对工程应用中的新型传感器进行校正，实践结果表明：使用该方法可较大幅度提高传感器获得真值的能力，提高CO2排放计量的准确度。