基于快速正交搜索算法的非线性预测控制

张 燕 申 森

(河北工业大学控制科学与工程学院，天津 300130)

快速正交搜索(Fast Orthogonal Search，FOS)算法能够最大限度地减小估算量相对于目标数据的均方误差[1]。与神经网络相比，FOS算法不是依靠耗时的迭代实现最小化，而是直接在一次迭代中就选择出合适的候选函数，并且计算出相应的系数。该算法的实现是在所有的候选函数中选择基础函数，能够使均方误差的减小量最大的候选函数被确定为合适的基础函数，并从候选函数中移除；在剩余的候选函数中重复上述选择过程，直到相应的停止条件满足时结束选择[2]。与普通的最小二乘法相比，FOS算法的优势是能够用更少的模型项建立一个精确的模型，模型项减少的同时也减小了噪声的干扰，从而使系统估算更为准确。目前，FOS算法已经有了很多的实际应用，包括递归滤波去除图像中的高斯噪声和脉冲噪声，语音信号的压缩，磁共振成像和正电子发射断层扫描，以及非线性系统的控制和基因的识别及其对治疗的反应的预测等[3]。

笔者从非线性预测控制的角度出发，利用FOS算法对非线性系统进行辨识，利用辨识模型建立预测控制器，实现基于FOS算法的预测控制。

1 FOS算法和系统辨识①

一个非线性系统可以表示为：

y(k)=F[y(k-1),…,y(k-N),u(k-1),…,

u(k-L)]+e(k)

(1)

式中e(k)——系统误差，数据记录的时间长度n=0,…,N；

F[·]——形式未知的连续非线性函数；

N、L——输入和输出的阶次；

y(k)——系统的输出。

在FOS算法中，式(1)可以进一步改写为：

Pm(k)=y(k-n1),…,y(k-ni),u(k-l1),…,

u(k-lj)

(2)

i≥0,1≤n1≤N,…,1≤ni≤N

j≥0,1≤l1≤L,…,1≤li≤L

式中am——Pm(k)的权值系数。

此时，系统的均方误差mse可以表示为：

上式上方的短横线表示数据记录在时间长度的平均值，该算法在所有的候选函数Pm(k)中进行搜索，选择对均方误差贡献最大的候选函数作为模型项，添加到构建的辨识模型当中。

为了实现这一搜索过程，首先要得到未知结构的非线性系统模型，利用格拉姆·施密特正交方法[4]，可以将式(2)改写为：

其中gm是wm(k)的权值，e(k)为误差，wm(k)是利用格拉姆·施密特正交方法将非正交函数Pm(k)正交化后得到的两两正交的函数序列。其计算过程具体如下：

(3)

其中正交系数：

(4)

此时系统的均方误差可以改写为：

(5)

正交函数的权值系数gm可以表示成：

这种正交方法的好处是它不需要输入上有自动校正功能，在数据记录的时间内没有引入任何误差。然而,正交函数的计算非常耗费时间，而且需要内存有相当大的数据存储空间[5]。

为了避免上述问题，FOS算法采用隐式正交法，不用单独计算出每一个正交函数wm(k)，只需计算出正交系数αmr。

因此，不用计算基础正交函数wr(k)就能得出式(4)的分子，类比式(3)可得：

(6)

同样，式(4)的分母可以表示成：

(7)

这样，αmr的值就可以通过式(6)、(7)计算出来。同理，式(5)的分子、分母也可以改写为如下形式：

(8)

(9)

从而gm就可以由式(8)、(9)计算出来。

根据式(5)可知，在增加第m个函数wm(k)后，均方误差mse的减小量可以表示为：

因此增加一个模型项后，剩余的均方误差mse可以表示成：

msem=msem-1-Qm

这就使得每一个非正交候选函数Pm(k)对系统均方误差的影响清楚地展现出来。在所有候选函数中，对应产生减小量Qm最大的一个被选为模型项，并从候选函数中去除。接下来算法继续在剩余的候选函数中重复上述搜索过程，直到停止搜索的条件满足时结束搜索。

停止的条件主要有：当系统的剩余误差达到足够小；一定数量的模型项已经被选出；剩余的候选函数不能使系统的误差产生足够的减小量[6]。

当搜索完成时，利用αmr和gm可以计算出被选出的模型项Pm(k)的系数am，即：

2 FOS算法步骤

通过上面的讨论，FOS算法将会不断搜索适合的候选函数直到一些预定义的停止条件得到满足为止。FOS算法的步骤为：

a. 将非正交候选函数序列Pm(k)经过隐式正交化后得到正交函数序列wm(k)；

b. 计算正交函数wm(k)的权值系数gm，计算每一个候选函数相对于均方误差的减小量Qm，选择Qm最大的候选函数作为模型项；

c. 重复步骤a、b，直到任何一个终止条件得到满足为止；

d. 由得出的gm和αmr递归计算am，完成对非线性系统辨识模型的构建。

3 基于FOS算法的预测控制

一个非线性系统可以表示为：

y(k)=F[y(k-1),…,y(k-N),u(k-1),…,u(k-L)]

式中F[·]——连续非线性函数[7]；

N、L——输入和输出的阶次。

函数模型通常是未知的，经过FOS算法进行辨识，可以得到一个新模型：

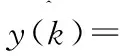
…+blu(k-l)

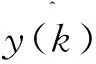
y(k+1)=a1y(k)+…+any(k-n+1)+b1u(k)+…+blu(k-l+1)

用yr(k+1)代替y(k+1)，yr(k+1)为设定值的柔化序列，以期望辨识系统的输出逼近设定值，则上式可以改写成：

yr(k+1)=a1y(k)+…+any(k-n+1)+b1u(k)+…+blu(k-l+1)

可以得出：

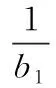
引入性能指标[9]为：

其中λ为控制加权因子。对性能指标进行滚动优化[10]，每次优化计算出u(k)，并将u(k)作为控制信号输入，计算出实际的输出y(k+1)。

4 仿真实例

选取非线性系统模型：

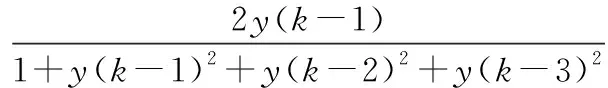
0.6u(k-1)+0.5u(k-2)

采用FOS算法进行训练时，模型项数量M=5，设定的输出序列为方波信号，柔化因子α=0.4。辨识结果如图1所示。

图1 系统辨识效果

利用上述辨识模型建立预测控制器，对非线性系统进行预测控制，同时与广义预测控制效果进行对比，结果如图2所示。

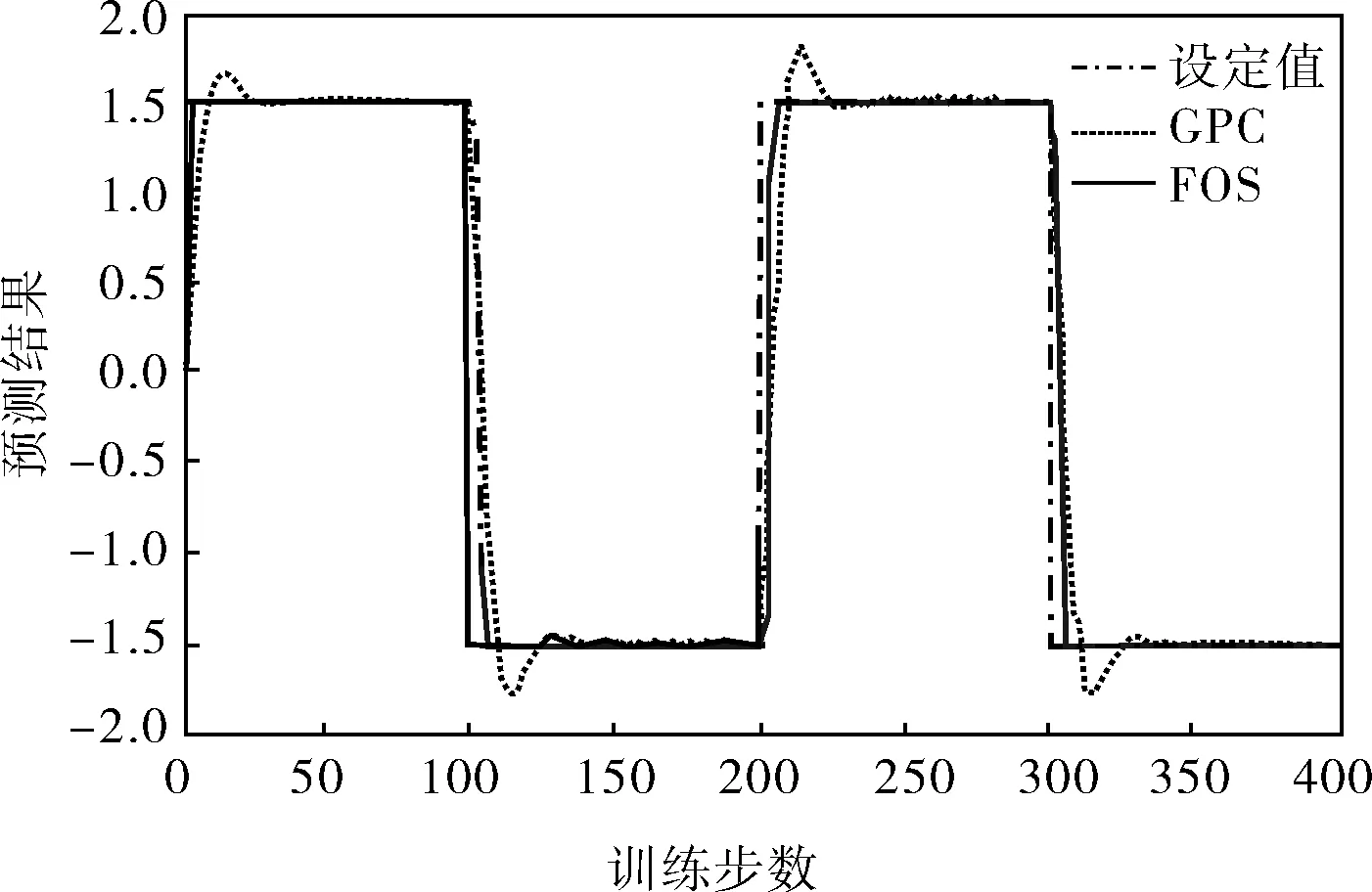
图2 预测效果

5 结束语

采用FOS算法对非线性系统进行辨识，从辨识的结果可以看出，FOS算法得出的估算模型对非线性系统有良好的跟随效果。利用估算模型建立预测模型，对系统进行闭环优化控制。通过对实际的非线性模型进行仿真实验，验证了所提方法的可行性和有效性。