怀来、延庆及其周边地区地壳介质各向异性研究*
2014-08-02邵媛媛郑需要
邵媛媛 郑需要
(中国北京100081中国地震局地球物理研究所)
怀来、延庆及其周边地区地壳介质各向异性研究*

(中国北京100081中国地震局地球物理研究所)
提出了利用人工爆破P波走时反演地壳介质方位各向异性参数的方法. 在假定介质是弱各向异性介质的情况下,使用扰动理论得到了线性化的反演公式,其中待反演的弱各向异性参数是P波走时的线性函数. 如果在反演公式中参考走时取相同震中距接收点的P波平均走时,那么所获得的弱各向异性参数与参考介质速度的选取无关. 反演得到的弱各向异性参数可以看作是不同震中距和不同深度范围内介质的等效弱各向异性参数. 等效弱各向异性参数在一定程度上反映了不同深度范围内水平方向相速度随方位的变化. 这种变化可能是不同时期构造应力作用的结果. 2007年中国地震局在首都圈怀来地区实施了一次大吨位人工爆破实验, 以爆破点为中心,布设了高密度的地震观测台网和台阵. 台站相对于爆破点具有360°的全方位覆盖,所得到的地震记录数据为研究怀来、 延庆地区地壳介质P波方位各向异性提供了必要条件. 我们通过走时反演获得了与水平方位相关的弱各向异性参数,并对弱各向异性参数进行坐标变换,得到了能够直观描述岩石弱各向异性的具有水平对称轴的横向各向同性介质,给出了对应的3个独立弱各向异性参数及其对称轴方位,讨论了介质各向异性与构造应力场的关系. 结果表明该地区地壳介质存在明显的方位各向异性,其最大值约为4.6%.
地壳介质 各向异性 地震射线 走时 反演
引言
地震各向异性广泛存在于地壳和上地幔(Crampin,1981; Babuska,Cara,1991; Helbig,1993). 沉积过程中形成的交互薄层结构会造成一种称为横向各向同性的各向异性(Thomsen,1986). 在构造应力场作用下,地壳中存在大量裂隙形成的定向优势排列,使地壳介质变成方位各向异性介质. 软流圈或地幔的对流或流动会引起由晶格定向排列形成的各向异性. 地壳及上地幔介质各向异性包含着大量关于构造运动的信息,为判断岩性、 应力状态和推断构造演化历史等提供了宝贵的资料. 地壳与上地幔各向异性研究关系到地震活动、 板块运动、 地球动力学和深部结构等众多地球物理基本问题. 因此地震各向异性的观测和研究已经成为人们探测地球内部信息的重要工具.
早在20世纪60年代,Hess(1964)在太平洋地区发现垂直于洋中脊的Pn波传播速度较其平行于洋中脊方向上的传播速度快. 为了解释这一现象,Backus (1965) 首次推导出了在任意弱各向异性介质中P波相速度的近似方程. Dziewonski和Anderson (1981,1984) 在建立全球地球模型(PREM)时引入各向异性,结果表明在上地幔220 km深度范围内存在2%—4% 的偏振各向异性.许多学者在欧洲、 美洲和亚洲等的许多国家都普遍观测到了地壳介质各向异性和剪切波分裂现象(Crampin,1978; Crampin,Evans,1985).

从20世纪70年代开始,在首都圈地区广泛开展了地震监测和探测研究工作. 该地区布设着我国最先进、 最密集的区域数字地震台网. 许忠淮等(1979)根据1960—1977年京津唐张地区地震的P波初动方向资料求出平均节面,给出本区域构造应力场最大主压应力轴方向为NE65°—75°. 许向彤等(1997,2001)利用怀来数字地震台网的记录资料,根据P波初动数据得到怀来ML4.1地震的震源机制断层面解,确定主压应力轴的方位角为236°,倾角为48°,与华北构造应力场一致. 戴维·布思和王培德(1997)在延庆—怀来盆地进行地震学合作研究,确认了横波分裂和介质各向异性现象的存在,分裂的横波快波的偏振取向为NE60°,与区域构造应力场方向一致. 金安蜀等(1980)利用当时北京地区台网远震P波到时数据,用ACH方法(Akietal,1977)反演了北京地区地壳和上地幔三维P波速度结构, 揭示了北京地区地壳和上地幔三维P波速度结构存在明显的横向不均匀性. 孙若昧和刘福田(1995)及孙若昧等(1996)利用京津唐地区1984—1991年地震P波到时资料和1986—1993年地震S波到时资料,分别对该地区的P波速度结构和S波速度结构进行层析成像反演,发现这一地区的历史地震震中在上地壳的投影大多分布在高速块体内或高速与低速块体的相交地带,且偏高速体的一侧. Huang和Zhao(2004) 采用地震层析成像方法反演得到研究区内详细的三维P波地壳速度结构模型.他们发现华北平原、 太行山和燕山隆起区内速度结构变化特征明显不同. 齐诚等(2006)选用华北地震遥测台网和首都圈数字化地震遥测台网1993—2005年记录的2866个地震事件的P波和S波到时资料,在充分考虑人工地震研究成果(嘉世旭等,2005)的基础上,计算得到了水平分辨率为25—50 km的首都圈地区地壳三维P波和S波速度结构,并获得了泊松比分布. 在上述这些成果中,研究人员主要是研究首都圈地区地壳和上地幔各向同性介质中的P波或S波速度结构,很少涉及介质的各向异性问题. 在研究首都圈地区的地壳各向异性问题时,许多研究人员都是通过对S波分裂的研究获得该地区地壳介质的各向异性(高原等,1995; 赖院根等,2006; 吴晶等,2007).
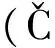

图1 怀来、 延庆地区地震台站及P波走时插值点分布图
1 方法
一般情况下,地壳介质是弱各向异性介质(Thomsen,1986).如果取各向同性介质作为参考介质,那么弱各向异性介质可以用密度归一化弹性参数aijkl描述如下:
(1)
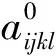

(2)
其中
(3)
如果波的传播方向定义为n=(cosφsinθ, sinφsinθ, cosθ),其中,φ是方位角,θ是波传播方向与z轴的夹角(0≤φ≤2π, 0≤θ≤π),则
(4)
(5)

(6)
(7)

对于qP波,m=3,方程(5)中被积分函数可以表示为
(8)
式中
(9)

考虑均匀弱各向异性介质,在这种情况下,将式(8)带入式(5)可以得到均匀介质中qP波的反演公式(Zheng,2004):
(10)

如果仅仅研究介质的方位各向异性,可令θ=90°,这时n=(cosφ, sinφ, 0),则式(9)变为
(11)
式(10)变为
(12)
从式(12)可以看出,介质的P波方位各向异性完全由5个各向异性参数决定,待反演的介质各向异性参数是P波走时的线性函数,而且与参考介质无关. 应该指出,这里的方位各向异性并不是HTI介质的方位各向异性,而且对称轴也不一定在水平面内. 因为式(12)中包含了比HTI更多的两个各向异性参数ε16和ε26. 为了获得最接近于HTI介质的3个各向异性参数(εx,εy,δz)及其对称轴的方位,我们使用Zheng(2007)所提出的方法.
假设HTI介质所在的坐标系为(x′,y′,z′),相应的弱各向异性参数为(ε′x,ε′y,δ′z),一般的方位各向异性介质所在的坐标系(x,y,z)中,z′与z轴重合. 将HTI介质通过绕z轴旋转某一角度φ,可以得到一般介质的弱各向异性参数(εx,εy,δz,ε16,ε26)(Zheng, 2007) :
(13)
方程(13)左边为一般介质的弱各向异性参数(已知量),求解式(13)便可以得到最接近的HTI介质参数ε′x,ε′y,δ′z及对称轴所在方位φ.
2 数据处理
考虑到地震台站相对于炮点的分布密度及其均匀程度随震中距的增大而减小,我们仅仅对以炮点为中心,某一半径范围内的地震台站记录进行分析和处理,共获得169个初至清晰的P波走时数据(其中震中距Δ<160 km的有82个台站,160<Δ<170 km的有8个台站,170<Δ<400 km的有71个台站,其它台站Δ>400 km). 由于大部分台站布设在山区,仅有少数台站位于平原,台站高程数据差别大,而且空间分布不均匀,所以我们使用怀来—延庆地区三维速度模型(嘉世旭等, 2005)对P波走时数据进行了高程校正,然后使用Delaunay三角网插值(Aurenhammer,1991; Okabeetal,2000)得到了几组以炮点为中心的不同震中距同心圆上的多方位P波走时数据(图1中红色十字). 图1中蓝色三角形代表具有清晰P波初至的台站,红色圆点为炮点. 在以炮点为中心,半径为170 km的区域内,根据原始台站的密度分布,得到了8个同心圆,其半径依次为40,50,60,80,100,120,140和150 km(图1). 每个同心圆上的插值个数为30,相邻插值点的方位角间隔为12°. 首先从研究区域的三维模型中对相同深度的不同节点速度进行平均,得到相应深度的速度. 根据不同深度的速度建立一个一维速度模型. 利用ANRAY标准射线追踪程序计算射线终点落在每一个同心圆上的射线路径,射线穿透的最大深度依次约为4,5,6,7,8,9,13和15 km(图2),其射线追踪积分步长为0.1 s. 对于每一个相同震中距的同心圆,使用一维速度模型中的射线路径及其沿路径的P波速度计算相应路径的P波平均速度. 在后面计算相速度随方位的变化时,P波平均速度将被用作参考各向同性速度.

图2 射线路径垂直剖面投影图
我们仅仅研究介质的方位各向异性. 由于射线路径与震中距密切相关,不同震中距的射线路径,特别是射线穿透深度有较大的差异. 为了研究不同震中距和射线穿透深度对介质各向异性的影响,我们需要对每一同心圆上P波走时分别进行分析和处理. 尽管我们已经进行了P波走时的高程校正,但是地壳浅部的横向非均匀性还会对方位各向异性造成一定的影响. 为了降低横向非均匀性对方位各向异性的影响,将研究地区以炮点为中心全方位360°平分为相等的两个区域,对这两个区域的每一个同心圆上的走时数据分别按两个区域进行反演,并计算观测值和反演值的总误差. 然后,以10°为步长转动平分线,重复同样的计算,获得误差随方位的变化. 通过误差分析,发现沿-10°和170°的平分线所得误差最小,所以,后面所有计算都是针对这一平分线分开的两个区域进行的. 其中-10°—170°(沿顺时针方位)的区域被称为W1区,170°—350°(沿顺时针方位)的区域被称为W2区.
如果介质是横向均匀的,那么就没有必要将研究区域划分为两个分区. 在这种情况下,由于其具有对称性,使用单一区域或者联合使用两个区域的走时数据进行反演所得结果是相同的. 反演公式(12)除了弱各向异性条件的假设外,对研究区域的每一点都成立. 然而在本研究中,反演所得介质方位各向异性参数仅具有平均意义. 这是由于所使用数据的空间覆盖不完备性造成的. 所以使用这种单一炮点的数据集,想获得研究区域各点介质的各向异性是不可能的. 从图1,2 可以看出,终点在同一同心圆的射线从炮点出发,沿弯曲路径到达某一最深点,然后继续沿几乎对称的路径到达接收点,所以反演得到的各向异性参数可以看作同心圆柱体内介质的平均(或等效)各向异性参数.
3 各向异性参数反演

根据反演得到的各向异性参数,我们计算了对应不同震中距范围,不同区域的P波等效相速度曲线. 在计算中使用了同心圆对应最大穿透深度以上的P波平均速度作为参考各向同性速度. 图3a--h分别给出了W1区(-10°,170°)内震中距为40, 50, 60, 80, 100,120, 140和150km时的等效介质P波相速度曲线; 图4a--h分别给出了W2区(170°,350°)内震中距为40,50,60,80,100,120,140和150 km时的等效介质相速度曲线. 从图3,4 中可以看出,大部分相速度曲线具有两个极大值,极大值对应的方位角随射线穿透深度的增加而变化. 由于P波相速度的极大值通常对应于最大主压应力方向,所以主压应力最大值的方向也随着射线穿透深度的变化而变化. 相速度的两个不同极大值可能代表不同构造时期主压应力的方向.W1区(-10°,170°)相速度极大值主要分布在65°或130°左右,W2区(170°,350°)相速度极大值主要分布在180°或210°左右. 总体来说此结果与华北区域的构造应力场的NE,EW方向大体一致.

表1 W1区域(-10°, 170°)内弱各向异性参数反演值

表2 W2区域(170°, 350°)内弱各向异性参数反演值

表3 整个区域内的反演的弱各向异性参数
通过反演,我们得到了与x-y平面(水平面)相联系的5个WA参数,它们代表了一般的弱各向异性介质. 为了获得与一般各向异性介质最接近的HTI介质,我们根据式(13)得到了HTI介质参数ε′x,ε′y,δ′z及其对称轴所在方位φ.
为了解反演结果的精度,图5和图6分别给出了W1区和W2区P波“观测”走时(“+”)和反演理论走时(实线). 走时的平均误差分别为0.134 s和0.104 s,最大误差分别为0.208 s和0.158 s. 产生误差的原因很多,其中最重要的误差来自地壳介质的横向非均匀性,另一种误差可能是由于拾取震相的不准确造成的. 根据所使用的地震仪器的采样率(100 sps), 这种误差可能为几十毫秒,所引起的各向异性参数的误差大约为千分之几.

图3 W1区(-10°,170°)内与震中距40 km (a)、 50 km (b)、 60 km (c)、 80 km (d)、 100 km (e)、 120 km (f)、 140 km (g)和150 km (h)相对应深度内的等效介质相速度曲线 实线表示通过反演得到的一般弱各向异性介质的相速度; “+”表示由“观测”走时计算得到的相速度; 虚线表示由坐标变换和最小二乘算出的相应的相速度; 红色直线代表P波相速度的参考各向同性速度

图4 W2区(170°,350°)内与震中距为40 km (a)、 50 km (b)、 60 km (c)、 80 km (d)、 100 km (e)、 120 km (f)、 140 km (g)和150 km (h)相对应深度内的等效介质相速度曲线 实线表示通过反演得到的一般弱各向异性介质的相速度; “+”表示由“观测”走时计算得到的相速度; 虚线表示由坐标变换和最小二乘算出的相应的相速度; 红色直线代表P波相速度的参考各向同性速度
4 讨论与结论


图5 W1区(-10°,170°)走时拟合图. 实线 表示反演值,“+”表示“观测值”
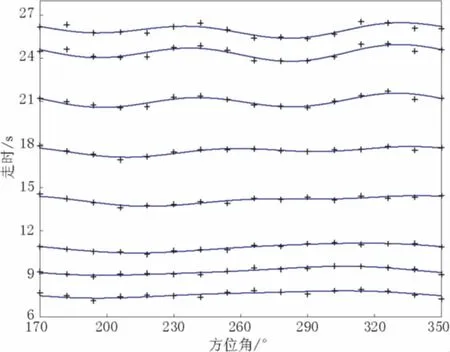
图6 W2区(170°,350°)走时拟合图. 实线 表示反演值,“+”表示“观测值”
戴维·布思,王培德. 1997. 延庆-怀来盆地地震预测研究[J]. 国际地震动态,(3): 1--12.
Booth D C,Wang P D. 1997. Earthquake predictions studies in the Yanqing--Huailai basin[J].RecentDevelopmentsinWorldSeismology,(3): 1--12 (in Chinese).
高原,郑斯华,孙勇. 1995. 唐山地区地壳裂隙各向异性[J].ActaSeismologicaSinica,17(3): 283--293.
Gao Y,Zheng S H,Sun Y. 1995. Anisotropy of crust cracks in Tangshan area[J].ActaSeismologicaSinica,17(3): 283--293 (in Chinese).
嘉世旭,齐诚,王夫运,陈棋福,张先康,陈颙. 2005. 首都圈地壳网格化三维结构[J]. 地球物理学报,48(6): 1316--1324.
Jia S X,Qi C,Wang F Y,Chen Q F,Zhang X K,Chen Y. 2005. Three-dimensional crustal gridded structure of the Capital area[J].ChineseJournalofGeophysics,48(6): 1316--1324 (in Chinese).
金安蜀,刘福田,孙永智. 1980. 北京地区地壳和上地幔的三维P波速度结构[J]. 地球物理学报,23(2): 172--182.
Jin A S,Liu F T,Sun Y Z. 1980. Three-dimensional P velocity structure of the crust and upper mantle under Beijing region[J] .ChineseJournalofGeophysics, 23(2): 172--182 (in Chinese).
赖院根,刘启元,陈九辉,刘洁,李顺成,郭飙,黄志斌,2006. 首都圈地区横波分裂与地壳应力场特征[J]. 地球物理学报,49(1): 189--196.
Lai Y G,Liu Q Y,Chen J H,Liu J,Li S C,Guo B,Huang Z B. 2006. Shear wave splitting and the features of the crustal stress field in the Capital Circle[J].ChineseJournalofGeophysics,49(1): 189--196 (in Chinese).
齐诚,赵大鹏,陈颙,陈棋福,王宝善. 2006. 首都圈地区地壳P波和S波三维速度结构及其与大地震的关系[J]. 地球物理学报,49(3): 805--815.
Qi C,Zhao D P,Chen Y,Chen Q F,Wang B S. 2006. 3-D P and S wave velocity structures and their relationship to strong earthquakes in the Chinese capital region[J].ChineseJournalofGeophysics,49(3): 805--815 (in Chinese).
孙若昧,刘福田. 1995. 京津唐地区地壳结构与强震的发生: Ⅰ. P波速度结构[J]. 地球物理学报,38(5): 599--607.
Sun R M,Liu F T. 1995. Crust structure and strong earthquake in Beijing,Tianjin,Tangshan area: Ⅰ. P wave velocity structure[J].ChineseJournalofGeophysics,38(5): 599--607 (in Chinese).
孙若昧,赵燕来,吴丹. 1996. 京津唐地区地壳结构与强震的发生: Ⅱ. S波速度结构[J]. 地球物理学报,39(3): 347--355.
Sun R M,Zhao Y L,Wu D. 1996. Crust structures and strong earthquakes in the Beijing,Tianjin,Tangshan area: Ⅱ. S wave velocity structure[J].ChineseJournalofGeophysics,39(3): 347--355 (in Chinese).
吴晶,高原,陈运泰,黄金莉. 2007. 首都圈西北部地区地壳介质地震各向异性特征初步研究[J]. 地球物理学报,50(1): 209--220.
Wu J,Gao Y,Chen Y T,Huang J L. 2007. Seismic anisotropy in the crust in northwestern capital area of China[J].ChineseJournalofGeophysics,50(1): 209--220 (in Chinese).
许向彤,陈运泰,王培德. 1997. 怀来盆地的构造应力场[J]. 地震地磁观测与研究,18(1): 1--8.
Xu X T,Chen Y T,Wang P D. 1997. Tectonic stress field in Huailai Basin[J].SeismologicalandGeomagneticObservationandResearch,18(1): 1--8 (in Chinese).
许向彤,陈运泰,王培德. 2001. 1995年7月20日怀来盆地ML4.1地震序列震源参数的精确测定[J]. 地震学报,23(3): 225--238.
Xu X T,Chen Y T,Wang P D. 2001. Precise determination of focal parameters for July 20,1995ML=4.1 earthquake sequence in the Huailai Basin[J].ActaSeismologicaSinica,23(3): 225--238 (in Chinese).
许忠淮,刘玉芬,张郢珍.1979. 京、 津、 唐、 张地区地震应力场的方向特征[J]. 地震学报,1(2): 121--132.
Xu Z H,Liu Y F,Zhang Y Z. 1979. On the characteristic of direction of the earthquake stress field around the Beijing area[J].ActaSeismologicaSinica,1(2): 121--132 (in Chinese).
Aki K,Christoffersson A,Husebye E S. 1977. Determination of the three-dimensional seismic structures of lithosphere[J].JGeophysRes,82(2): 277--296.
Aurenhammer F. 1991. Voronoi diagrams: A survey of a fundamental geometric data structures[J].ACMComputingSurveys,23(3): 345--405.
Babuska V,Cara M. 1991.SeismicAnisotropyintheEarth[M]. Dordrecht: Kluwer Academic Publishers: 1--3.
Backus G E. 1965. Possible form of seismic anisotropy of the upper-most mantle under oceans[J].JGeophysRes,70(14): 3429--3439.
Crampin S. 1978. Seismic-wave propagation through a cracked solid: Polarization as a possible dilatancy diagnostic[J].GeophysJRastrSoc,53(3): 467--496.
Crampin S. 1981. A review of wave motion in an isotropic and cracked elastic-media[J].WaveMotion,33(4): 43--91.
Crampin S,Evans R. 1985. Analysis of records of local earthquakes: The Turkish Dilatancy Projects (TDP1 and TDP2)[J].GeophysJRastrSoc,83(1): 1--16.
Dziewonski A M,Anderson D L. 1981. Preliminary reference Earth mode1[J].PhysEarthPlanetInter,25(4): 297--356.
Dziewonski A M,Anderson D L. 1984. Seismic tomography of the Earth’s interior[J].AmericaScientist,72(5): 483--494.
Helbig K. 1993. Simultaneous observation of seismic waves of different polarization indicates subsurface anisotropy and might help to unravel its cause[J].JApplGeophys,30(1/2): 1--24.
Hess H H. 1964. Seismic anisotropy of the upper mantle under oceans[J].Nature,203: 629--631.
Huang J,Zhao D. 2004. Crustal heterogeneity and seismotectonics of the region around Beijing,China[J].Tectonophysics,385(1/2/3/4): 159--180.
Mensch T,Rasolofosaon P. 1997. Elastic wave velocities in anisotropic media of arbitrary anisotropy: Generalization of Thomsen’s parameters,ε,δandγ[J].GeophysJInt,128(1): 43--64.
Okabe A,Boots B,Sugihara K,Chiu S N,Kendall D G. 2000.SpatialTessellations:ConceptandApplicationsofVoronoiDiagrams[M]. Chichester: John Wiley & Sons,Inc.,1--671.
Thomsen L. 1986. Weak elastic anisotropy[J].Geophysics,51(10): 1954--1966.
Zheng X. 2004. Inversion for elastic parameters in weakly anisotropic media[J].GeophysJInt,159(3): 1077--1089.
Zheng X. 2007. Identification of symmetry planes in weakly anisotropic elastic media[J].GeophysJInt,170(1): 468--478.
Crustal anisotropy of Huailai--Yanqing region in North China

(InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China)
A method for inversion of seismic anisotropy in crustal medium is presented by using the P-wave travel times from an explosive source. Perturbation theory is used to derive the linear inversion formulae when the medium is taken as a weakly anisotropic (WA) medium. The WA parameters in the formulae are a linear function of the P-wave travel time. The WA parameters are independent of the reference velocity when the reference travel time takes an average of P-wave travel times. The WA parameters from inversion can be considered as effective anisotropic parameters concerning the medium within different source-distances and different depths,which reflect the variation of phase velocity with azimuth. The azimuthal variation of phase velocity was probably caused by the tectonic force in different history periods. A large exploration was carried out in Huailai--Yanqing region near Beijing by China Earthquake Administration in 2007. A high density seismic network was deployed around the explosive point with azimuthal coverage of 360°,which provides an abundant data set for studying P wave seismic anisotropy of crustal medium. Travel time tomography in weakly anisotropic medium was used to calculate WA parameters. In order to get a comprehensive understanding of the studied medium,the inverted WA parameters were transformed to a new coordinate system related to a HTI (transverse isotropy with a horizontal axis of symmetry) medium. Three WA parameters and the orientation of symmetry axis of the medium were obtained. The relation of the WA parameters to tectonic stress field was discussed. The result shows that there exists an obviously azimuthal anisotropy (maximum 4.6%) in the crust of studied region.
crust medium; anisotropy; seismic ray; travel time; inversion
10.3969/j.issn.0253-3782.2014.03.005.
国家自然科学基金重大项目(41090292)和面上项目(40974050)资助.
2013-04-11收到初稿,2013-06-06决定采用修改稿.
e-mail: xuyaozheng@aliyun.com
10.3969/j.issn.0253-3782.2014.03.005
P315.3+1
A
邵媛媛,郑需要. 2014. 怀来、 延庆及其周边地区地壳介质各向异性研究. 地震学报, 36(3): 390--402.
Shao Y Y, Zheng X Y. 2014. Crustal anisotropy of Huailai--Yanqing region in North China.ActaSeismologicaSinica, 36(3): 390--402. doi:10.3969/j.issn.0253-3782.2014.03.005.
