基于数学形态学的正序基波谐波检测方法

李向新,张颖,刘美容

(1.湖南省电力公司邵阳电业局，湖南 邵阳 422000；2.长沙理工大学电气信息与工程学院,湖南 长沙 410114;3.湖南师范大学物理与信息科学学院,湖南 长沙 410081)

基于数学形态学的正序基波谐波检测方法

李向新1，2,张颖2,刘美容3

(1.湖南省电力公司邵阳电业局，湖南 邵阳 422000；2.长沙理工大学电气信息与工程学院,湖南 长沙 410114;3.湖南师范大学物理与信息科学学院,湖南 长沙 410081)

在非线性负荷特性及电力系统电压突变情况下，提出一种新的谐波检测方法，即基于数学形态学的正序基波谐波检测方法。该方法在数学形态学基础上，通过选取合理的扁平结构元素的结构及长度，运用形态学的膨胀和腐蚀运算对电力系统的谐波进行运算处理。在电力系统信号存在高斯噪声干扰条件下，该方法能快速、准确地检测出电力系统中的谐波频域分量和较好地滤除电力系统信号中的高斯噪声，有较好的谐波检测效果。在Matlab/simulink仿真平台上，通过实例验证了该方法是有效的。

数学形态学；正序基波检测；滤波；谐波检测；形态滤波器；

1 引言

近年来，随国家“十二五计划”重大战略部署，国家能源及电力行业大力发展新能源分布式发电、环保生物质发电及发展节能型超高压柔性技术输电等，引进了许多大功率电力电子元器件及非线性开关器件。当电力系统运行和控制、铁路电气化、工厂生产及家庭电器的使用，产生大量的谐波，加剧了电能质量受到严重污染，引起电网中的功率不平衡及谐波等严重问题，给电网的稳定安全、经济运行带来了巨大的隐患，同时也给电力电子技术的发展带来了巨大的障碍。既然给电力系统运行带来安全隐患，也不利于节省能源，研究可靠的滤波器和解决电能质量污染源问题是国家根据现代电网战略发展和智能电网发展的要求。

在许多的谐波智能检测方法中，每种方法都有自己的优点和缺点。如瞬时无功谐波检测方法的优点是电路简单易懂、受频率扰动小、电路原理极易实现，实时性佳，延时性小，应用的范围和前景比较广，在设计滤波器中，瞬时无功功率检测方法存在检测存在相位延时性，控制运算算法复杂，检测精度不高，在电压或者负载存在不平衡的条件下会出现下，会出现谐波检测不精确，不能很好的去除噪声。当前，主要有如下几种谐波检测方法：基于小波分析的谐波检测方法[1]，由于小波分析算法计算的时候具有计算量大，很大的冗余度，运算速度慢等缺点；基于傅里叶变换的谐波检测方法[2]，傅里叶在频率变换的时候存在局部性差，检测的精度不高，不灵敏等特点，极易给检测带来很大的误差，导致可靠性不高；人工神经网络的谐波检测方法[3]，人工神经网络算法的网络结构复杂，占有运算空间复杂及运算量大等缺点，且神经网络算法研究的不够成熟；基于遗传算法的谐波检测方法[4]，遗传算法存在较差的计算稳定性，同时运算量大，具有只能局部处理信号波形的缺点；基于瞬时无功功率理论的谐波检测方法[5]，在文献[5]中，谐波检测方法原理简单易懂，在电网三相不平衡的前提下，或者电压收到扰动和突变时，不能准确的检测电网中的谐波分量，同时在对电压波形携带噪声检测的效果也分成差；基于自适应的谐波检测方法[6]，该算法不能精确检测谐波分量，存在检测不稳定性。为此，本文提出了一种基于数学形态学的正序基波谐波检测方法，准确地检测出电力系统中的谐波分量。

2 数学形态学滤波基本原理

2.1 基本概念

在处理数学图像及信号中，其中有一种有效的方法—数学形态学，它是数学领域的一种拓扑分支。它是以集合和几何领域的一门基础学科，提出一种名为“刺探”的结构元素，其作用是对电网实时数据进行光滑和缝合信号的局部特征，修正处理采集信号，使电网运行更加稳定。针对采集的信号，加以类比处理，提出合理及优越的信号特性，近几年中，数学形态学主要应用在图像处理、继电保护、电能质量及扰动监测中，利用数学形态学的拓扑结构元素去处理电力系统采集信号，并加以数学运算，滤除噪声，提出优质及有用的信号。

设计滤波的结构元素，利用数学形态学的拓扑结构进行运算，如腐蚀、膨胀、开运算及闭运算[7]，假设从电网提取的信号为一维离散信号函数，利用数学形态学对信号进行分析和处理，滤波优化电力系统信号。

2.2 腐蚀和膨胀运算

从电力系统实时采集信号，假定从电网系统采集的信号f(n)为一维离散函数信号，g(n)为对电网信号处理运算而设的拓扑结构元素。f(n)信号函数针对结构元素g(n)的膨胀运算和腐蚀运算[8]分别定义为:

(f⊕g)(n)=max[f(n+m)+g(n)]

(1)

(fΘg)(n)=min[f(n+m)-g(n)]

(2)

n=0,1,2,…,k-L;m=0,1,2,…,L-1，且k≥L，腐蚀及膨胀运算中参数k、L为结构元素的长度。数学形态学的腐蚀运算是对电网信号进行扩张变换，而腐蚀运算则是对电网信号进行收缩转换，腐蚀和膨胀运算是数学形态学的两种基本运算。

2.3 开运算和闭运算

数学形态学有两种不同而且不可逆运算方式：闭运算和开运算[9]。开运算是对采集的信号进行先腐蚀后膨胀，其处理光滑信号，锐化毛刺和孤立点；然而闭运算则是先膨胀后腐蚀，缝合信号上小洞和裂缝，在结构元素g(n)条件下，针对电网采集的信号f(n)，数学形态学的开、闭运算分别定义为:

(f∘g)(n)=(fΘg⊕g)(n)

(3)

(f•g)(n)=(f⊕gΘg)(n)

(4)

2.4 数学形态滤波算法

因为数学形态学运算是不可逆的，将数学形态学的开、闭运算和膨胀、腐蚀运算相结合，分别对信号函数进行不同方式的处理，产生不同的处理效果，由此可以设计出效果不同的形态滤波器。为了得到不同效果的波形图，可以将数学形态学的膨胀、腐蚀、开和闭运算算法[10]进行采取不同的联级处理，就会使电网的信号更加光滑平稳，出去毛刺，缝合信号的漏洞。其滤波结构如下面三种方式，其中电网采集信号为f(n)，结构元素为g(n)，经过形态滤波后的输出用yn表示，其运算如下：

(1)交替滤波器：

oc(f(n))=(f∘g•g)(n)

(5)

co(f(n))=(f•g∘g)(n)

(6)

(2)混合滤波器

[(f)mix(g)](n)=(f•g∘g)(n)/2

(7)

(3)交替混合滤波器

Yn=[oc(f(n))+co(f(n))]/2

(8)

当电网信号受到干扰时，处于暂态突变和扰动时或者三相不平衡时，采用联级交替混合滤波器，多次采取数学形态处理信号，提高检测精度。

2.5 结构元素的选择

对信号进行处理时，选取合理的结构元素，能使滤除谐波的效果达到最佳状态，其关键是对结构函数的形态和长度进行研究。在对电网信号处理时，电网中的三次和五次谐波对检测的干扰很大，同时也影响动态响应和速度。结构元素形状和长度的选取对数学形态运算量有很大影响，结构越复杂，其运算量也越大。一般选取圆、扁平结构、三角函数等作为结构元素。本文结构元素为半圆，其半径取值在幅值的1/50～1/10之间，其滤波的效果达到最优，利用开闭运算的同时，根据前后两个采样信号的差值来适当调整结构元素的长度和宽度，半圆的半径越小，则检测的精度越高。同时数学形态学对信号进行处理，使其波形更加的光滑。

3 正序基波谐波电流检测方法

3.1 正序基波提取器的原理

针对电力系统中的电压突变及电力系统非线性负荷特性，提出基于数学形态的正序基波谐波检测方法，能精确地谐波的频域分量和较好的滤除波形图中的噪声源。正序基波原理是将电力系统中负载的ua，ub，uc投影到新的αβ坐标系下，获得理想的电压向量uα和uβ。设uα为正弦函数信号为e(t)=Asin(ω1t+φ)，运用幅值积分变换将uα转换为信号函数y(t)=Asin(ω1t+φ)t。再将正弦信号函数uα经过延时90°运算后，可以获得辅助信号函数x(t)=Asin(ωt+φ)。运用拉普拉斯变换将三个信号函数进行处理运算，提取系统中的正序基波电压信号[11]。该运算转换具有较好的选频特性，其α-β坐标转换过程如图1所示。

图1 α-β坐标系下实现原理图

在图1中的α-β轴上，将拉普拉斯变换后的信号函数进行整合，构建新的空间结构，信号函数的表达式分别为ya(t)=Asin(ω1t+φ)t和yβ(t)=Asin(ω1t+φ)t。其正序基波提取器的结构和原理如图2所示，K为比例放大系数，其作用是调整输出信号函数的幅值大小。

根据电力系统中的电压突变情况及非线性负荷特性，提取正序基波电压。这个运算方式存在对电力系统的基频存在偏差时不敏感，但是能准确地提取基波信号等优点。

图2 正序基波提取器原理图

3.2 锁相环PLL电路原理

锁相电路具体作用是来实时跟踪电力系统中的幅频特性参数，并锁定电力系统中电压与电力的空间相角。在电力系统电压突变或电力系统波形图严重畸变情况下，设计合理的结构，不会对电力系统中检测谐波运算响应有延时，同时也提高了电力系统谐波检测的精度和运算处理速度。提取电力系统中的基波电压和电流之间的相位角结构原理图如3所示，其控制电路过程如图3所示。

图3 锁相环PLL的原理

在电力系统非线性不平衡负荷及电压波形突变情况下，合理地设计锁相环PLL电路结构，实时追踪电网的电压基波波形的频率和相角，能提高运算处理的速度和响应。其数学转换表达式为：

p3φ=uaia+ubib+ucic=uabia+ucbic

(9)

3.3 正序基波谐波检测原理

在电力系统非线性负荷特性及电压突变情况下，构建新的空间提取正序基波电压，能精确地提取电力系统中的信号。正序基波电压的谐波检测原理是在对偶p-q理论和瞬时无功功率理论上发展而来的。其实质是将电力系统中的电压向量ua、ub、uc转换为新空间αβ坐标系中的uα和uβ向量，与电力系统中的PLL采集的实时电流向量iα和iβ相乘积，获得理想的辅助功率p和q。利用空间的逆运算，通过cpq-abc获得电力系统中理想的三相电压输出为ua，ub，uc。基于数学形态学的正序基波谐波检测原理框图如图4所示。

图4 正序基波谐波检测原理图

在图4中的cαβ-pq的转换过程中，其数学转换表达式为下:

(10)

在图4中的cpq-αβ转换过程中，提取系统中的得到正序电压，其数学转换表达式为下：

(11)

在图4中的cαβ-abc逆变换过程中，获得理想的三相电压。其数学转换表达式为：

(12)

4 仿真分析

在仿真软件matlab/simulink的平台上塔建谐波检测模型，对谐波检测法进行仿真，设电网仿真参数为：电力系统中非线性负载三相相电压un=1V，电网基波频频ω=50Hz，采样周期为fs=10000Hz，采样周期为八个周期，即采样点数为1600点。则假设电力系统中的谐波表达式为：ih(t)=0.41cos(3ωt+30°)+0.17cos(5ωt+60°)+0.14cos(7ωt+45°)+0.15cos(11ωt+90°)+0.11cos(13ωt+60°)，加入2%的噪声源，其具体的仿真电路检测图如图5所示。

图5 正序基波谐波检测仿真图

在图5中，ub、ub、uc为电网三相电压源，iah，ibh，ich分别所注入电网谐波分量参数，电力系统中的电阻及电感参数分别为Rs=1Ω，Ls=1e-3H。

根据电力系统谐波的频率域幅值特性，选取瞬时无功功率谐波检测方法和自适应滤波谐波检测方法分别与基于数学形态学的正序基波谐波检测方法相比较。

图6 电网三相基波电压图

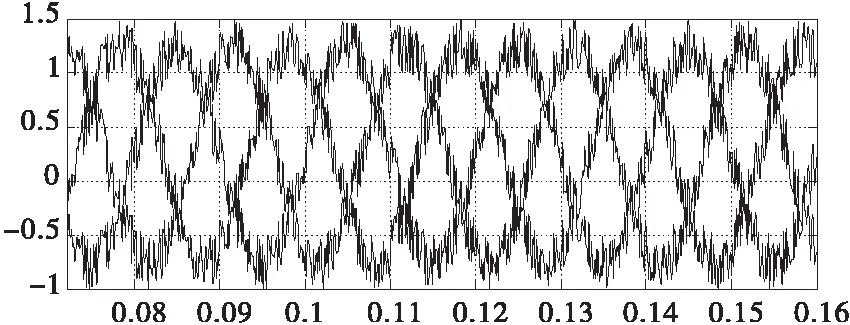
图7 电网含有谐波波形图

图8 瞬时无功功率检测方法仿真

图9 LMS算法检测仿真

图10 基于数学形态学的正序基波方法仿真

图7为含有谐波a相电流波形图，图8为瞬时无功检测谐波仿真，在0.06s时波形图才达到理想的波形图，且三相电流的幅值大小不同及波形图中还含有噪声分量。图9为LMS算法谐波检测的仿真，在0.04s时波形图达到光滑，且波形图中含有噪声分量。图10为基于数学形态学的正序基波谐波检测的仿真，在0.04s时波形图达到光滑，且三相波形对称及很好地滤除波形图中的噪声分量。通过分析和比较三种算法的仿真，验证了基于数学形态学的正序基波谐波检测的滤波效果较好。

图11 瞬时无功功率的FFT分析

图12 LMS算法检测的FFT分析

图13 基于数学形态学的正序基波检测的FFT分析

图11为瞬时无功功率谐波检测FFT分析图，该方法只能检测出谐波中的三次谐波分量，且三次谐波的幅值只有0.2左右，与所设值的误差较大。图12为LMS算法谐波检测的FFT分析图，该方法只能检测出谐波中的三次、五次和七次谐波分量，且幅值的大小分别为0.2、0.09和0.05，与所设值的误差也较大。图13为基于数学形态学的正序基波谐波检测的FFT分析图，该方法不仅能检测出三、五、七次谐波分量，也能检测出十一和十三次谐波分量，且对谐波幅值检测的误差较小，谐波幅值的大小分别为0.39、0.21、0.14、0.1和0.07。通过三种算法的FFT分析，验证了基于形态学正序基波谐波检测方法能精确地检测谐波频率和幅值。

5 结论

在电力在电力系统非线性负荷特性及电压突变情况下，针对一些算法不能很好地对电力系统中的谐波分量进行检测及补偿，提出基于数学形态学的正序基波谐波检测方法。该方法通过构建新的坐标空间，提取电力系统中的正序电压量，通过设计合理的结构元素和PLL的结构原理，采用数学形态学滤波器运算处理。在Matlab/simulink平台上进行实例仿真，验证了该方法能很好地滤波分量，也能精确地检测出电力系统中的谐波频域分量及对谐波的运算处理速度响应也快。

[1] 杜天军,雷勇,等.基于混叠补偿小波变换的电力系统谐波检测方法[J].中国电机工程学报,2005,25(3):54-60.

[2] 刘开培,张俊敏.基于DFT的瞬时谐波检测方法[J].电力自动化设备,2005,23(3):23-27.

[3] 汤胜清,程小华，等.一种基于多层前向神经网络的谐波检测方法[J].中国电机工程学报,2006,26(18):90-94.

[4] 张俊敏,田微，等.基于瞬时无功功率理论谐波检测方法的研究[J].电力系统保护与控制,2008,36(18):33-36.

[5] 盘宏斌，罗安，等.一种改进的基于最小二乘法的自适应谐波检测方法[J].中国电机工程学报,2008,28(13):144-151.

[6] 崔屹.图象处理与分析-数学形态学方法及应用[M]科学出版社.

[7] 曾纪勇,丁洪发，等.基于数学形态学的谐波检测与电能质量扰动定位方法[J].中国电机工程学报,2005,25(21):21-27.

[8] 孙浩云,牟龙华，等.自适应形态学滤波器在HAPF中的应用研究[J].电力系统保护与控制,2011,39(3):41-44.

[9] OU Yang-hua,Bu Le-ping.“Voltage sag detection based on Dq transform and mathematical morphology filter”[J].Procedia Engineering,2011,volume,23:775-779.

[10] 郝晓弘,田江博，等.基于信息熵和数学形态学的电压跌落持续时间检测方法[J].电力系统保护与控制,2012,40(11):30-35.

[11] 张桂斌,徐政，等.基于空间矢量的基波正序、负序分量及谐波分量的实时检测方法[J].中国电机工程学报,2001,21(10):1-5.

[12] 袁川,杨洪耕.三相电压畸变且不对称时电流基波正序有功分量的改进瞬时检测方法研究[J].继电器,2005,33(14):57-60.

Positive Sequence Harmonic Detection Method Based on Mathematical Morphology

LIXiang-xin1,2，ZHANGYing2，LIUMei-rong3

(1.Shaoyang Electric Power Bureau ,Electric Power Co. of Hunan Province,Shaoyang 422000,China;2.College of Electrical and Information Engineering,Changsha University of Science & Technology,Changsha 410014,China;3.College of Physics and Information Science,Hunan Normal University,Changsha 410081,China)

In view of the nonlinear load characteristic and power system voltage mutation,this paper puts forward a new method of harmonic detection,a positive sequence fundamental harmonic detection method based on mathematical morphology.Based on mathematical morphology,this mehod chooses reasonable structure and flat structure elements of length,uses the expansion and corrosion of the morphology to process the harmonic in power system.Under the condition that power system signal is disturbed by gaussian noise,the method can quickly and accurately detect the harmonic frequency component in the electric power system and better filter gaussian noise signals in power system,which presents good effect in harmonic detection.In Matlab/simulink simulation platform,the examples prove the effectiveness of this method.

mathematical morphology；positive sequence fundamental wave detection；filter；harmonic detection；morphological filter

1004-289X(2014)02-0020-05

TM71

B

2013-05-07