微波处理中木材内温度分布模型的热源反演1)

刘 畅 王行建 曹 军

(东北林业大学，哈尔滨，150040)

微波处理中木材内温度分布模型的热源反演1)

刘 畅 王行建 曹 军

(东北林业大学，哈尔滨，150040)

从微波处理木材中木材内部温度分布的热传导模型出发，将单向微波照射与双向微波照射时的模型划归为一类模型来求解。利用求解一维波动方程的方法并定义新算子反演微波处理中木材内部温度分布模型的热源表达式。研究结果表明：单向微波与双向微波处理中木材内部温度分布的模型所反演的热源可以相应地由定义的自伴算子的特征根和特征向量统一表示。

热源反演；木材；温度分布

According to the heat conduction model of temperature profiles in wood during microwave heating, the models of unilateral microwave heating and bilateral microwave heating should be classified as a model to solve by solving the wave equation and defining new operator inverting the model of temperature profiles in wood during microwave heating. The heat source of unilateral microwave heating and bilateral microwave heating should be expressed by eigenvector and characteristic root of the operator. The heat source identification of heat conduction equation which is similar to the model of temperature profiles in wood during microwave heating can be solved by using our method to invert the expression of heat source.

在木材加工生产过程中尤其是人造板工艺过程中，存在着大量热交换的过程，热交换对于工艺过程影响很大，直接决定了产品的质量，随着对木材加工工艺过程热传递机理的不断研究，生产中传热现象逐渐被刻画称为数学模型进行定性分析。热传递过程主要来自外部作用和内部作用两个方面，微波处理也已经成为先进的热处理技术，同时在工艺过程中存在复杂的物理化学变化，释放大量热，这些热源也影响着木材处理和产品质量，热源影响的分析成为进一步研究木材处理的方法。

微波处理木材中木材内部温度分布与微波辐射的方式直接相关，利用伯朗定律建立了单向微波与双向微波处理时木材内部温度迁移的模型，揭示微波处理中木材内部温度分布的规律，即当采用单向微波辐射与双向微波辐射时，木材内部温度分布的模型可由一类一维热传导方程表示，由热传导方程进一步认为沿微波入射方向，单向微波照射时，木材内部温度逐渐降低；双向微波辐射时，木材内部的温度分布梯度是外低内高的。对于此类一维热传导方程的热源识别问题，不同的学者提出了不同的解答方法，如有限差分法、迭代法等。对于以上的方法，学者得出了含有只依赖于时间变量热源的一维热传导问题的热源识别方法，而对于微波处理木材时木材内部温度分布模型一类的一维热传导方程，其热源是只依赖于空间变量的，对其进行热源识别就与含有只依赖与时间变量的热传导方程的热源识别有很大的区别。本研究揭示了处理含有仅依赖于空间变量的热源的一维热传导方程热源识别问题的方法与规律，以期为此类热源识别问题的解答提供理论依据。

1 模型处理及热源反演

微波处理木材时，假设木材为均质材料，研究表明，单向微波辐射时，木材内部温度分布梯度是沿着微波入射方向先增加后急剧降低的，设微波入射方向为x方向，木材微波入射表面为y方向，且木材在x方向所处区间为[0,d]，若设室温为T0，得到木材内部温度分布随时间变化的热传导方程：

式中：c为单位体积木材的热容量；λ为木材导热系数；T为T(x,t)，即木材中的温度分布；t为时间；q0为单位体积木材吸收的功率，可通过微波发生装置进行调节；x为微波入射木材的深度；b为木材对微波的吸收系数，一般为常数。

采用上述两种不同方式处理木材时，方程的表达形式是一致的，仅仅是边界条件不同。划归统一的热传导方程为：

T(x，0)=T0。

(1)

式中：Tt为温度分度对时间的一阶偏导；Txx为温度分布对深度的二阶偏导；f(x)为所要反演的只依赖于空间变量x的热源。

两种方程只有边界条件不同，故下面以单向微波辐射时木材内部温度分布模型的边界条件为例：

α(T(0，t)-T0)=λTx|x=0；

α(T(d，t)-T0)=-λTx|x=d。

(2)

式中：α为空气的对流传热系数；Tx为温度分布对深度的一阶导数。

1.1 模型处理

微波处理木材中，木材内部温度的分布与微波加热的方式直接相关[1]。采用单向微波辐射时，沿着微波的入射方向，木材内温度先增加后急剧下降，均匀性较差，采用双向微波辐射时，木材内的温度先增加后减小，均匀性较好。根据上述热传导规律，建立以上微波加热木材中木材内部温度分布的模型，要实现此类模型的热源识别，先对其进行处理[2]，关于T(x,t)的混合边界条件不是齐次的，那么选取一个与T(x,t)具有相同边界条件的辅助函数w(x,t)和一个新的未知函数V(x,t)，将T(x,t)表示为：

T(x，t)=V(x，t)+w(x，t)。

因为w(x,t)与T(x,t)具有相同的边界条件，所以新未知函数V(x,t)的边界条件就已经是齐次的了。将泛定方程(1)转化为V(x,t)的泛定方程：

(3)

初始条件：

V(x，0)=0。

(4)

边界条件：

(5)

(6)

将主函数V(x,t)由(6)表示为：

(7)

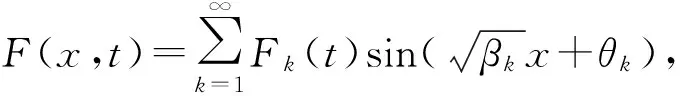
(8)

构建以下拉普拉斯变换：

LFk(t)=F(x)。

代入方程(8)中解得：

式中：dτ为积分微元。

研究模型中的主函数可以表示为：

1.2 热源反演

模型中给出的条件是特殊的，为了揭示此类一维热传导方程热源反演的规律，给出一般的初始条件：

T(x，0)=φ(x)。

则有：

定义新的算子Q[4]，则对任意φ∈L2(0，t)，记Φ(x)=φ(x)-T0，将算子Q作用在Φ(x)上，有：

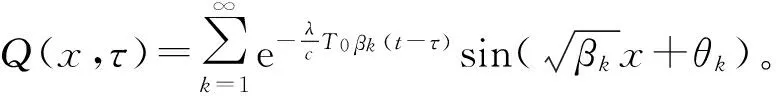
Q为L2(0，t)到L2(0，t)的线性紧自伴算子，其特征根可以表示为：

与特征根对应的特征向量为：

则热源反演问题转化为求解以下算子方程：

Qf(x)=φ(x)。

(9)

由皮卡定理得：

2 结论

研究了微波加热木材时木材内部温度分布模型的热源识别问题。在已有建立微波加热木材时的模型的基础上，对模型进行处理，将单向光照射和双向光照射时的模型划归为一类模型来求解。采用了波动方程求解时的方法，将一维波动方程的解法运用到了热传导方程上，求解出函数Xk(x)。再利用拉普拉斯变换和拉普拉斯逆变换求出主函数，最后通过定义新的算子，反演出热源函数。从而通过求解统一模型来求得未知热源。本研究揭示了处理含有仅依赖于空间变量的热源的一维热传导方程热源识别问题的方法与规律，给出了研究此类热源反演问题的一种方法并为此类问题的研究提供理论依据。

[1] 李贤军,张璧光,李文军，等.微波真空干燥过程中木材内部的温度分布[J].北京林业大学学报,2006,28(6):128-131.

[2] 陆立柱.第一二三类非齐次线性边界条件的齐次化[J].山西师范大学学报：自然科学版,2001,15(4):17-20.

[3] 张云生.数学物理方程中的分离变量法[J].工科数学,1993,9(1):8-9.

[4]KirschA.AnIntroductiontotheMathematicalTheoryofInverseProblems(AppliedMathematicalSciences)[M].北京:世界图书出版公司北京公司,1999.

Heat Source Inversion of Temperature Profile Model in Wood during Microwave Heating/

Liu Chang, Wang Xingjian, Cao Jun

(Northeast Forestry University, Harbin 150040, P. R. China)//Journal of Northeast Forestry University.-2014,42(8).-131～132,156

Heat source inversion; Wood; Temperature distribution

刘畅，女，1990年8月生，东北林业大学理学院，硕士研究生。

王行建，东北林业大学计算机科学与技术学院，工程师。E-mail：jianxingwang@126.com。

2013年10月14日。

S781.7

1) 中央高校基本科研业务费专项资金项目(DL13AB01)。

责任编辑：戴芳天。