Hilbert空间中的g-Riesz基序列

黄喜娇,杨永燕

(安阳师范学院人文管理学院 建筑工程学院，河南 安阳 455000)

自1952年Hilbert空间中的框架概念被提出后，框架理论至今已经取得了丰硕的成果[1-2].由于框架的定义和Riesz基序列的定义之间联系密切，一些学者对Riesz基序列的性质进行了研究.2002年，P.G.Casazza和O.Christensen等[3]对Hilbert空间中的Riesz基序列的性质进行了研究.之后，李登峰、董立华等[4-5]对Hilbert空间中的Riesz基序列做了进一步的研究.2006年，孙文昌[6]首次引入了g-框架概念，随后g-Riesz基、g-Riesz框架、g-框架序列、g-Riesz-Fischer序列、g-Besselian框架等陆续被学者研究，并且取得了一系列重要的成果[6-11]，但是对Hilbert空间中的Riesz基序列的研究较少.本文引入g-Riesz基序列的概念，对g-Riesz基序列的性质进行了研究，并利用g-Riesz基序列的性质证明了g-Riesz基的稳定性.

1 预备知识

定义4[6]设Λj∈L(U,Vj),j∈J, 则称序列{Λj}j∈J为U关于{Vj}j∈J的g-Riesz基.如果序列{Λj}j∈J满足以下两个条件：

①{Λj}j∈J是g-完备的，即{f∈U:Λjf=0,j∈J}={0};

②存在正数A,B>0, 使得对任意有限子集J1⊂J和gj∈Vj,j∈J, 有

则称A,B为g-Riesz基的上、下界.

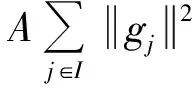
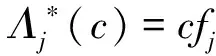
2 主要结果及证明

定理1序列{Λj}j∈J为U关于{Vj}j∈J的g-Riesz基序列，界为A,B当且仅当可定义有界线性算子

(1)

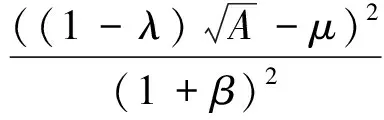
证明设序列{Λj:Λj∈L(U,Vj)}j∈J为U关于{Vj}j∈J的g-Riesz基序列，界为A,B，则对任意有限子集I⊂J，gj∈Vj，有

(2)

由(1) 和(2)式得

有关g-框架的稳定性，孙文昌在文献[7]中已经做了讨论，本文将利用下面的引理1及引理2，用不同的方法证明g-Riesz基的稳定性.

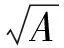
则{Γj}j∈J为U关于{Vj}j∈J的g-框架,且框架界为

(3)

引理2[8]令Λj∈L(U,Vj),j∈J，则下列两个条件等价：

①序列{Λj}j∈J是U关于{Vj}j∈J的g-Riesz基，界为A,B;

文献[11]中有如下结果：

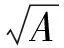
本文给出推论1的另一个证明方法：

证明由引理1和引理2,可以得到{Γj}j∈J为U关于{Vj}j∈J的g-框架，其界由(3)式给出.由g-框架的左边不等式可以得到

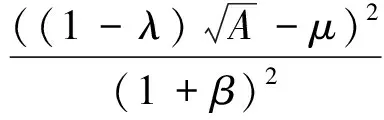
参考文献：

[1] Christensen O. An Introduction to Frames and Riesz Bases[M]. Boston:Birkhǎuser, 2003.

[2] Casazza P G. The art of frame theory[J]. Taiwanese J of Math, 2000,4(2):129-201.

[3] Casazza P G, Christensen O, Linder A. Riesz-Fischer sequences and lower frame bounds[J]. Z Anal Anwend, 2002,21(2):305-314.

[4] 李登峰，薛明志.Banach空间上的基和框架[M].北京:科学出版社,2007:68-71.

[5] 董立华,姜曰华,张玉坤.关于Riesz-Fischer序列[J].烟台师范学院学报：自然科学版,2003,19(1):10-13.

[6] Sun W. G-frames and g-Riesz bases[J]. Math Anal Appl, 2006,322(1):437-452.

[7] Sun W. Stability of g-frames[J]. Math Anal Appl, 2006,326(2):858-868.

[8] Ding M L, Zhu Y C. G-Besselian frames in Hilbert spaces[J]. Acta Mathematica Sinica：English Series, 2010,26(11):2117-2130.

[9] 李建振,朱玉灿.Hilbert空间中的g-Riesz框架[J].中国科学:数学,2011,41(1):53-68.

[10] 黄喜娇,朱玉灿.Hilbert空间中的g-Riesz-Fischer序列的扰动[J].三明学院学报：自然科学版,2012,29(4):12-16.

[11] Zhu Y C. Characterizations of g-frames and g-Riesz bases in Hilbert spaces[J]. Acta Mathematica Sinica：English Series, 2008,24(10):1727-1736.