多学科优化中的近似模型及其在艇体结构优化中的应用

许 辉, 周 奇

(中国舰船研究设计中心，湖北 武汉 430064)

多学科优化中的近似模型及其在艇体结构优化中的应用

许 辉, 周 奇

(中国舰船研究设计中心，湖北 武汉 430064)

近似技术是多学科设计优化关键技术之一。系统介绍多学科设计优化中常用的3种近似模型：响应面模型(Response Surface Methodology，RSM)、Kriging模型、径向基函数(Radical Basis Function，RBF)模型。对比分析3类近似模型在典型数学函数不同维度下的拟合性能。结果表明，Kriging模型的综合拟合性能最优，RBF模型次之，RSM拟合性能不佳。在此基础上，通过拉丁超立方试验设计选取样本点，基于Kriging模型构造潜艇平行舯体某舱段耐压壳体结构响应的近似模型，应用粒子群优化算法完成了耐压壳体结构轻量化设计。最优化设计方案质量较初始方案减少了11.99%。

近似模型；拟合性能；粒子群优化；潜艇壳体；拉丁超立方试验

0 引 言

目前，在舰船研制领域各学科相继引进了各类先进的设计分析工具，如结构学科的Ansys，Abaqus，Nastran等；快速性学科的Fluent，Cfx、Shipflow等；耐波性学科的HYDROSTAR等；操纵性学科的Shipma，Napa等。这些设计分析工具的使用极大提高了设计效率和分析精度。然而，在进行多学科设计优化过程中，通常需要很多次迭代才能得到最优结果。数值仿真软件在进行学科计算时，需要花费巨大的时间成本，这种基于数值仿真模型的多学科优化求解，其计算耗时往往是设计者无法接受的。

自20世纪80年代Kleijnen提出近似模型概念以来，构建近似模型成为解决以上问题的有效途径。Hefazi等[1]为快速性子学科构造响应面近似模型完成了三体船总体概念多学科优化设计；Lam等[2]将Kriging模型应用于机翼气动/结构多学科设计优化问题中，有效地验证了近似模型在实际工程中的应用价值；宋保维等[3]在鱼雷外形优化设计中采用基于试验设计的响应面方法构造阻力系数比的二次响应面近似模型，设计出符合工程实际的鱼雷外形；孙凯军等[4]采用拉丁超立方抽样试验设计方法得到样本点，并建立Kriging模型替代费时的流动模拟，进行高超声速舵面平面形状优化设计；容江磊等[5]基于Kriging模型建立跑车尾翼断面数学模型，在近似模型上进行全局寻优，较大改善了跑车的空气动力学性能。

耐压壳作为潜艇核心设备的保护体，一旦耐压壳出现结构破损，耐压舱室进水，将引发各电子仪器、电池的短路失控，甚至发生电机击穿导致整个电控系统毁灭以致潜艇失事的恶性事故，同时壳体重量、壳体结构尺寸对潜艇运行的平稳性、快速性都起重要作用[8]。因此，研究合理的耐压壳结构是潜艇总体设计中的结构学科专家所关心的重要问题。

本文介绍多学科设计优化中常用的3种近似模型：响应面近似模型(ResponseSurface Methodology，RSM)、Kriging模型及径向基函数(Radical Basis Function，RBF) 模型，对比分析3种近似模型对数学测试函数不同维数的拟合性能。然后，基于Kriging模型进行潜艇平行舯体某舱段耐压壳体结构响应的近似模型：输入变量的选取；以拉丁超立方试验设计生成样本点；基于ABAQUS进行的有限元建模与仿真分析；应力响应的提取及近似模型的全局与局部误差检验。最后，应用粒子群优化算法完成了耐压壳体结构轻量化设计。

1 多学科近似模型

近似方法是通过插值或者拟合来构造近似模型，利用已知样本数据来预测未知响应的数学方法。其构建过程主要如下：

1)筛选合适的设计变量

选定对输出响应影响较大的输入参数x=[x1,x2…xn]，并确定参数的上下限[xlow,xup]。

2)通过试验设计方法选取样本点

常用的试验设计方法有全因子试验(Full Factorial Design，FFD)、中心组合试验(Central Composite Design，CCD)、正交数组试验(Orthogonal Arrays Design，OAD)、拉丁超立方试验设计(Latin Hypercube Design，LHD)等。

3)近似模型的构建与精度检验

在试验设计选定的样本点下，通过数学解析或仿真等获取样本点下的响应值，选取合适的近似模型，构建近似模型并进行精度分析。

目前，多学科设计优化领域常用的近似模型主要包括RSM模型、Kriging模型和RBF模型。

1.1 响应面近似模型

响应面近似技术是数学方法和统计方法结合的产物，他通过多项式回归表达式，依托最小二乘法来建立输入变量与响应之间的函数表达式，是目前多学科设计优化中常用的近似方法。

多项式响应面模型的基本形式如下：

(1)

式中：d为响应面的最高阶数；β0，βi，βij…βii…i为逼近系数，通过最小二乘法求得。将样本点的值代入响应面模型中，使得响应的预测值与真实值之间的误差平方和最小。

β=[XTX]-1XTY。

(2)

式中：X=[X1…Xn]T；Xi为样本点xi的分量与β次序对应构成的行向量；Y为由样本点的响应值组成的列向量。

1.2 Kriging近似模型

Kriging模型是一种估计方差最小的无偏估计模型，它通过相关函数的作用，具有局部估计的特点。最早由南非地质学家Krige于1951年提出，并用于矿产资源的分布预测。后经由sack等引入工程应用领域。

Kriging模型一般表示为[6]：

(3)

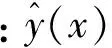
Cov[z(xi),z(xj)]=σ2R[R(xi,xj)]。

(4)

式中：R(xi,xj)为样本点xi,xj之间的相关函数；R为对称相关矩阵。相关函数有不同的形式，实际工程应用中，以Guassian函数最为常见：

(5)

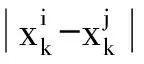
(6)

式中：Y为由样本点的响应值组成的列向量；F为n维列向量，当式中的g(x)简化为常数时，F为单位列向量；rT(x)为n维列向量，代表预测点与样本点之间的相关性，即：

rT(x)=[R(x,x1),R(x,x2),…R(x,xn)]T。

(7)

(8)

(9)

式(9)中描述的未知参数θk可通过极大似然估计方法求得，即：

(10)

通过上述无约束优化问题的求解，可得到最优拟合的Kriging模型。

1.3 径向基函数近似模型

径向基函数是一类以待测点与样本点之间的欧氏距离为自变量的函数，其基本形式为[7]：

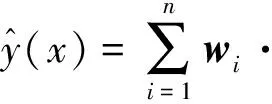
(11)

式中：w(x)=[w1,w2…,wn]T为权重系数；φ=[φ(r1),φ(r2),…，φ(rn)]T；ri=‖x-xi‖描述样本点与待测点之间的欧氏距离。常用的径向函数有多二次函数、逆多二次函数、薄板是径向函数，样条函数和高斯函数等。本文选用高斯函数，其数学表达式为：

(12)

式中δ为高斯函数的宽度。

待测点权系数使在满足插值条件f(xj)=yj(j=1,2…n)下，通过转换式求得：

w=φ-1·Y。

(13)

式中：

φ=[φij]=[φ(‖xi-xj‖)],Y=(y1,y2…yn)T。

2 三类近似模型的评价分析

2.1 评价指标

为了合理评价多学科设计优化中的3种近似模型的全局和局部拟合性能，本文引入复相关系数和最大误差作为评价指标。

1)复相关系数R2

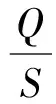
(14)

2)最大误差δME

(15)

δME反应近似模型局部拟合精度。其值越小，表明近似模型局部拟合性能越好。

2.2 典型函数不同维数下三类近似模型拟合精度

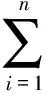
(16)

设计变量范围为-1≤xi≤1。

当n=1时，采用拉丁超立方设计试验方法在设计空间选取12个样本点，分别运用RSM模型、Kriging模型、RBF模型对f(x)进行设计空间内的拟合，同时，在[-1,1]区间内随机产生24个检验点对3种模型进行精度检验。图1所示为n=1时3种近似模型拟合效果。

图1 n=1时三类近似模型对测试函数拟合效果Fig.1 Three approximate model fitting results for n=1

由图1可看出，与函数解析值相比较，RBF模型与Kriging模型拟合效果较好，RSM模型拟合程度稍微欠缺，但偏差度不大。

为探讨三类近似模型对不同复杂度函数的拟合能力及发展趋势，对比了维数n=1至n=5时，等样本情况下三类近似模型拟合的拟合精度。图2和图3分别为三类近似模型的最大误差δME和复相关系数R2。

图2 三类近似模型对测试函数不同维数下拟合最大误差Fig.2 Maximum error of three approximate models

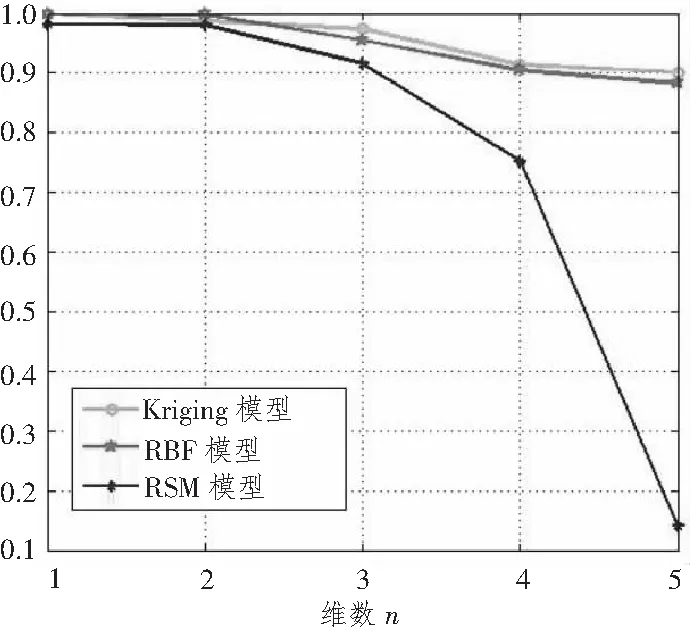
图3 三类近似模型对测试函数不同维数下拟合复相关系数Fig.3 Multiple correlation coefficient of three approximate models

由图2和图3可看出：

1)随着维数的增加，三类近似模型的拟合精度均不同程度的降低。其中，随非线性程度的增加，RSM模型拟合精度下降最明显，当n=5时RSM模型拟合最大误差达到60.518%，复相关系数降低至0.141，可认为拟合失败。RBF模型与Kriging模型稳定性比较接近。

2)相同维数下，Kriging模型的全局拟合能力和局部拟合能力略优于RBF模型，RSM模型拟合性能最差。

3 近似模型在潜艇耐压壳结构优化中的应用

3.1 潜艇耐压舱壳体结构优化模型

潜艇壳体结构设计的目的是在使壳体的强度和稳定性都满足要求的条件下，尽量节约材料，减少整个壳体的重量。本文讨论一型具有T型肋骨的水滴型核动力潜艇平行舯体某舱段壳体结构。已知壳体外径R=5.05 m，总长L=110.3 m，潜艇极限下潜深度h=530 m，耐压体采用HY-80高强度钢，其屈服极限σs=548.8 MPa，杨氏模量E=2.9×105MPa，泊松比u=0.3，密度ρ=7 750 kg/m3。设计变量为壳体厚度60 mm≤t≤80 mm，肋骨间距1 m≤l≤1.2 m。优化模型为：

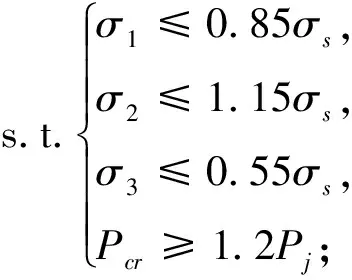
(17)

式中：σ1≤0.85σs和σ2≤1.15σs分别为壳体强度约束；σ3≤0.55σs为肋骨强度约束；Pcr≥1.2Pj为总体稳定性约束；Pj为壳体工作外载荷；σ1为肋骨跨距中点处壳板最大周向应力；σ2为肋骨处壳板横截面上的相当应力；σ3为肋骨应力；Pcr为壳板整体失稳时的实际临界压力。

3.2 潜艇耐压壳体结构Kriging近似模型构造

若在上述优化模型中，结构响应采用基于有限元的分析方法，在优化迭代过程中需反复求解新的分析方程，并计算每次结构参数修改后的性态响应，计算成本过大。由上节典型数学函数不同维数下的对比分析可知，Kriging模型的拟合性能在三类近似模型中最优，故选用Kriging模型训练和构建耐压壳体在均匀静水压力下各应力成分的近似模型。

通过LHD选取32个试验样本的，利用ABAQUS软件参数化建模，获取试验样本点下的响应值，建立输入变量与性态响应之间的近似关系。

为验证近似模型的拟合精度是否达标，在设计空间内随机选取一组样本点，综合Kriging模型给出的预测值和有限元方法获取真实响应值，求取Kriging模型的精度，整个过程如图4所示。表1给出了LHD(32)下各响应值的拟合精度结果。

表1 精度分析结果

由表1可知，基于Kriging近似模型给出的预测

图4 潜艇耐压壳体结构输出响应的近似模型构建与精度分析流程Fig.4 The flow chart of approximate models for shell hull of submarine

结果与有限元给出的预测结果一致性较好。潜艇耐压壳体各项性态响应值的复相关系数均接近1，精度能满足工程要求，可以用来优化设计。图5为肋骨跨距中点处壳板最大周向应力σ1与壳体厚度t，肋骨间距l形成的Kriging近似模型。

图5 σ1与t，l间的Kriging近似模型Fig.5 The approximate models betweenσ1，t，l

3.3 优化结果讨论

为了获取设计结果的全局最优解，采用粒子群优化算法(Particle Swarm Optimization，PSO)作为寻优策略。PSO通过模仿自然界中鸟类和鱼类群体觅食迁徙中，个体与群体协调一致的机理，通过群体最优方向、个体最优方向和惯性方向的协调来求解优化问题。优化参数设定为：粒子数目为20，最大迭代次数100次，加速因子c1和c2均取2，惯性权值w=0.9。优化结果与初始结果对比如表2所示。

由表2可看出，优化设计质量比初始设计质量降低11.99%。将优化结果带入有限元分析程序，验证了结构应力响应值满足强度与稳定性要求。表明优化设计方案有效可靠。

表2 优化结果

4 结 语

近似模型技术是解决复杂系统工程结构多学科设计优化的必要方法。其常用于优化迭代过程中替代高精度有限元仿真模型，获取优化设计的最优解。对三类常用的多学科近似模型进行拟合性能研究，对比分析其对典型函数不同维数的拟合精度，结果表明，Kriging模型的综合拟合性能最优、RBF模型次之，RSM拟合性能不佳。以粒子群优化算法完成潜艇耐压壳体结构优化设计，获得了满意的设计方案，为潜艇总体性能多学科优化奠定了一定的基础。

[1] HEFAZI H,MIZINE I,SCHMITZ A,et al.Multidisciplinary synthesis optimization process in multihull ship design[J].Naval Engineers Journal,2010,122(3):29-47.

[2] LAM X B,KIM Y S,HOANG A D,et al.Coupled aerostructural design optimization using the kriging model and integrated multiobjective optimization algorithm[J].Journal of Optimization Theory and Applications,2009,142(3):533-556.

[3] 宋保维,温庆国,毛昭勇,等.基于均匀试验响应面法在鱼雷外形设计中的应用[J].鱼雷技术,2009,17(6):19-23.

SONG Bao-wei,WEN Qing-guo,MAO Zhao-yong,et al.Application of response surface methodology based on uniform test to shape optimization design of torpedo[J].Torpedo Technology,2009,17(6):19-23.

[4] 孙凯军,宋文萍,韩忠华.基于Kriging模型的高超声速舵面优化设计[J].航空计算技术,2012,42(2):9-12.

SUN Kai-jun,SONG Wen-ping,HAN Zhong-hua.Optimization design of hypersonic control surface based on kriging model [J].Aeronautical Computing Technique,2012,42(2):9-12.

[5] 容江磊,谷正气,杨易,等.基于Kriging模型的跑车尾翼断面形状的气动优化[J].中国机械工程,2011,22(2):243-247.

RONG Jiang-lei,GU Zheng-qi,YANG Yi,et al.Aerodynamics optimization of cross sectional shape for a sports car′s rear wing based on kriging surrogate model[J].China Mechanical Engineering,2011,22(2):243-247.

[6] CHEN X,ANKENMAN B E,NELSON B L.Enhancing stochastic kriging metamodels with gradient estimators[J].Operations Research,2013,61(2):512-528.

[7] LI H,ZHONG M C,ZHANG C L,et al.Study on RBF network adaptive control for robot loading based on uncertainty compensation[J].Advanced Materials Research,2013,706:1042-1046.

[8] 邵开文，马运义.舰船技术与设计概论[M].北京：国防工业出版社,2005.

Approximation methods of multidisciplinary design optimization and their application in shell hull of submarine

XU Hui, ZHOU Qi

(China Ship Development and Design Center,Wuhan 430064,China)

Approximation method is one of the key technologies for multidisciplinary design optimization of vessels. In this paper,three commonly approximation methods,including response surface method,Kriging,radical basis function are introduced concise. A comparison of three approximation for their fitting performance is conducted through a typical mathematical functions with different dimensions.The results shows that Kriging,with its optimum comprehensive performance,is best suitable for replacing finite element model,the radical basis function is in the middle position,while the approximation performance of response surface is poor.Then, Sample points selected by latin hypercube experimental design method,and a Kriging medols are constructed for shell struct of submarine. Error analysis showed that the models can meet the engineering application requirements.Finally, The structural lightweight design results are proposed base on the particle swarm optimization.Optimized design program quality decrease 11.99% compared to the weight of the initial design scheme.

approximation models;fitting performance;particle swarm optimization;shell structure of submarine;latin hypercube design experimental

2013-12-02;

2014-05-15

国防基础科研重点资助项目

许辉(1980-)，女，工程师，从事舰船总体优化研究。

U661

A

1672-7649(2014)12-0006-05

10.3404/j.issn.1672-7649.2014.12.002