一类解析函数的系数不等式和卷积性质
2014-08-01李书海周海燕
李书海,周海燕
一类解析函数的系数不等式和卷积性质
李书海,周海燕
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文继续研究文[1]中引进的解析函数类,给出了该函数类的卷积定理以及系数不等式等新性质.
星象函数;Hdamard卷积;从属
1 引言
我们假定,本文中出现的λ,α,β均满足:λ>-1,0≤α<1,0≤β<1.
设A是单位圆U={z:|z|<1}内具有形式f(z)=z+a2z2+…的解析函数全体组成的类.S*(α),K(α),C(α)分别表示α级星象函数类、α级凸象函数类和α级近于凸函数类.
设给定实数λ>-1,用

定义算子Dλ,其中*表示Hadamard卷积.有展开式[1]:

令

和

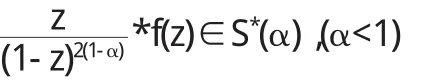
则称f(z)为α级预星象函数,其全体记作R(α).
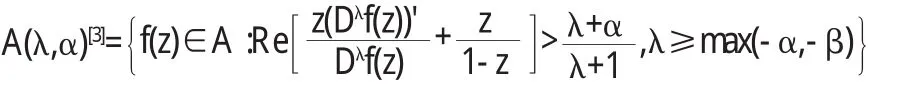
定义1[2]若函数f(z)∈A,满足条件
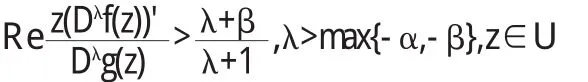
则称f(z)在B(λ,α,β)中.
作者在[1]中得到该族中函数的积分表达式;借助算子理论建立B(λ,α,β)的包含关系,讨论端点性质;证明族中函数的偏差定理.本文给出了B(λ,α,β)的卷积定理以及系数不等式等新性质.
2 Hadamard卷积
引理1[4]若
定义2[1]设f(z)∈A,若存在函数g(z)∈A(λ,α),满足条件
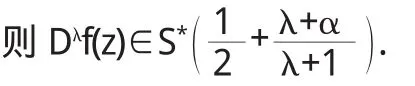
引理2[2]若ø(z)∈R(α),g(z)∈S*(α),p(z)在U内解析且有正实部,则
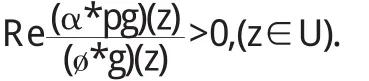
若Rep(z)>r,置Q(z)=p(z)-r,则Re(p(z)-r)>0,于是利用引理1不难证明:
引理3若α≤β<1,0
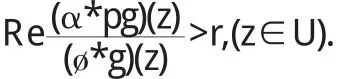
引理4[5]设ø(z)∈K(α),g(z)∈S*(α),若p(z)在U内解析且Rep(z)>r则
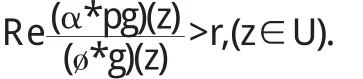
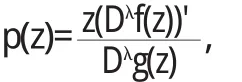
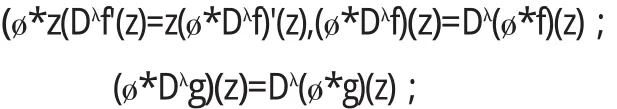
根据引理3,得到

证毕.
由引理1和引理4不难证明:
对于复数r,Rer≥0,取凸象函数
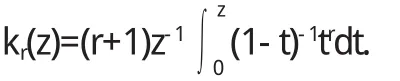
由定理2可得

3 系数不等式
引理5[3]若,则

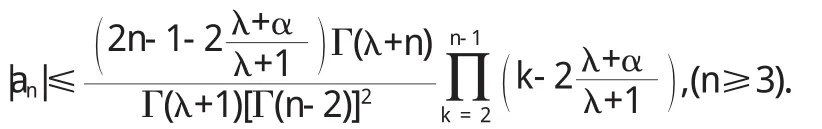
引理6[6]若在U内解析,且Rep(z)>0,则
从引理6容易得到:

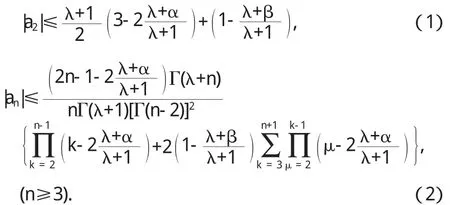

把
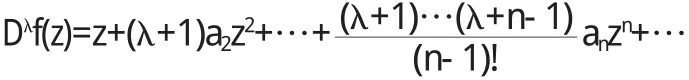
和
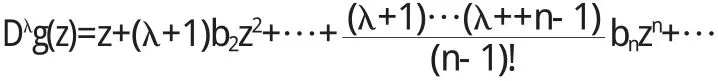
以及p(z)的级数展开式代入(3)式,即等式z(Dλf(z))'=p(z) Dλg(z)中,并比较z的同次幂的系数,得到

从(4)式推出

当n=2时,根据引理5和引理7,从(5)式推出
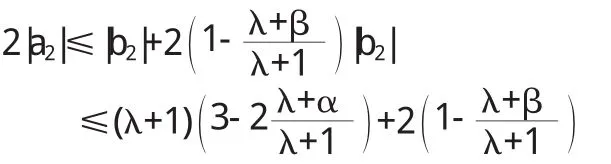
从上式即得(1)式;
当n=3,4,…时,根据引理5和引理7,从(5)式推出

推论2若

〔1〕李书海.一类新的解析函数族 [J].应用泛函分析学报, 2005,17(4):344-348.
〔2〕Ruscheweyh St.Linear operators between classes of prestarlike functions[J].Comment Math.,Helv.,1977,52: 497-509.
〔3〕赵业喜.线性同胚于星象函数的一族解析函数[J].数学学报,1997,40(3):385-394.
〔4〕赵业喜.线性同胚于星象函数的一族解析函数[J].数学进展,2000,29(1):26-28.
〔5〕Ruscheweyh St.and Sheil-Small,T.,Hadamard products of Schlicht functions and the Pólya-Schoenberg conjecture[J].Comm.Math.Helv.,48(1973):119-135.
〔6〕Ch.泊茂仁克著,杨维奇译.单叶函数[M].北京:科学出版社,1987.
O174.51
A
1673-260X(2014)10-0001-02
