基于ARGO浮标数据的全球海水声速场研究

蔡艳辉，程鹏飞，文汉江，杨希希，张金铎

(1.中国测绘科学研究院，北京 100830；2.国家测绘工程技术研究中心，北京 100039)

1 引 言

目前，水下目标的定位、导航最有效的手段还是声音信号。与通常的无线电测距的方式一样，通过测量声音信号往返或者单程的传播时间，在声音传播速度已知的条件下，就可以直接计算出两个目标的距离[1-2]。通常，海水声速当作一个已知量，但是，声音在介质中的传播速度与介质的特性有关，因此，海水介质的变化都将影响声速的大小。如何准确地确定海水声速的大小是进行水下精密测量的关键问题[3]，同时，海水声速变化会导致声线的弯曲，如果不能准确地确定海水声速的梯度，就不可能准确地确定声线的弯曲，也将导致不能够准确地改正声线的弯曲。另一方面，海水声速场也是分析海水信道、海水声场反演、海水声层析的基本工具。

海水声速是海水的一个固有属性，与海水的温度、盐度和压力直接相关，可以直接看成是温度、盐度和压力的函数，如果温度、盐度和压力发生变化，声速也就必然发生变化。由于太阳的照射，海洋表面的温度自然随纬度的变化而变化，同时，海流、洋流的变化，海风、海浪的作用，海水温度、盐度和压力的变化存在十分复杂的规律，既有系统性成分，也包含一定的随机性的成分，很难直接用一个数学模型直接表示全球的海水温度、盐度和压力的实变特性。这也就决定了海水声速同样具有一定的系统性和随机性。正视海水温度、盐度的这种性质，全球目前都是采用数值方法研究海水的温度和盐度[4-6]，通过构造海水声速与海水温度、盐度和压力的经验函数，间接研究海水声速的性质。

ARGO浮标就是通过实地测量海水上层的温度、盐度的剖面数据来研究海洋的变化。目前，全球大概有超过3000个ARGO浮标飘浮在各个大洋，实时提供温盐的剖面数据[7]。通过这些实测的数据，可以研究全球海水的温度、盐度的变化，构造全球的海水温度、盐度模型。Reynolds采用OI的方法实现了ARGO浮标剖面数据和卫星辐射遥感数据同化，计算全球标准温度格网[8-10]；国内，王桂华等利用ARGO资料重构了太平洋的三维温度、盐度和流场[11]。目前，NOAA发布的SST(全球海水表面温度格网)数据，最主要的数据源就是来自ARGO的剖面数据。然而，基于ARGO浮标数据构造全球三维声速场的文献，目前还不是很多，相关的研究还比较少。本文则基于全球ARGO浮标观测的温盐剖面数据，提出了一种基于面球谐函数展开构造全球海水声速场的模型。通过对非标准的温盐剖面数据进行多项式曲线拟合，计算得到不同深度的全球观测数据，这样则可以计算不同深度的全球海水声速场。该模型可以很好地分析任意深度海水声速的水平分布梯度，可以非常方便地构造和反演水下声场。

2 海水声速映射模型

2.1 常用海水声速映射模型

海水的状态方程[1]：

dp=c2dρ

(1)

其中，ρ为任意一点的密度，p为任意一点的瞬时声压，c为声速。

(2)

其中，ρ,β分别为当前点水介质的密度和绝热压缩系统，海水中ρ,β又都是海水温度t、盐度s和静压力p的函数，因此，声速也是海水温度、盐度和静压力的函数。

c=V(t,s,p)

(3)

经过大量试验表明，海水中的声速的影响规律大概在温度增加1℃时，声速增加约4.15m/s；盐度每变化1‰，声速变化约1.13 m/s；深度增加1m，压力增加约0.1个大气压，声速增加约0.16 m/s。虽然声速可以表示为海水温度、盐度和静压力的函数，但是由于盐度又与温度和压力有关，完整地解析表达还比较困难，通常都采用经验公式进行数值计算。根据不同的试验数据，得到不同的经验公式，其中常用的海水声速经验公式包括Wilson公式(1960)、Leroy公式(1969)、Frye和Pugh(1971)、Del Grosso公式(1974)、Medwin公式(1975)、Chen和Millero公式(1977)、Mackenzie公式(1981)等人发表的公式[4-6，12-14]。由于经验公式都有自己的温度、盐度、压力(深度)适用范围，所以只能适用于特定的海洋区域，超出公式的范围，将导致数据错误。

温度可以通过温度传感器进行测量，盐度通常通过导电性测量而获得，静水压力由海水深度直接计算。Leroy和Parthiot(1998)给出了海水压力P与深度D的转换关系由下式给出：

(4)

国内水下工程上声速计算模型比较常用的是Medwin模型(1975)：

C=1449.2+4.6T-5.5×10-2T2+2.9×10-4T3+(1.34-0.01T)(S-35)+0.016D

(5)

其中，C为声速(m/s)，T为温度(℃)，S为盐度(1‰)，D为深度(m)，该公式的适用范围：0≤T≤35，0≤S≤45，0≤D≤1000。

该经验公式是Wilson公式(1962)的简化版，故成为Wilson简化公式。

根据我国海区的大量水文资料，《国家海道测量规范》(1998)中采用的经验公式[15]：

C=1449.2+4.6T-0.055T2+0.00029T3+(1.34-0.01T)(S-35)-0.017D

(6)

其中，C为声速(m/s)，T为温度(oC)，S为盐度(1‰)，D为深度(m)，该公式的适用范围：0≤T≤35，0≤S≤45，0≤D≤1000。该公式是Medwin公式的变形公式，只能用于近岸的浅水工程。

2.2 精密海水声速经验模型

联合国教科文组织(UNESCO)、国际科学理事会海洋研究科学委员会(SCOR)、国际海洋开发理事会(ICES)和国际海洋物理科学协会(IAPSO)共同采用了Chen和Millero(1977) 提出的海水声速经验公式[6]：

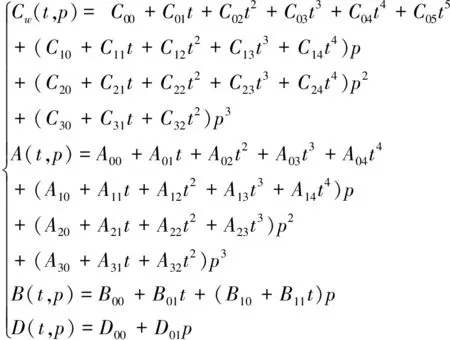
(7)

该经验公式使用42个系数(表1)将声速表示为温度、盐度和压力的五阶多项式，其模型精度达到0.19m/s。该模型的使用范围是：0≤s≤40psu，0≤t≤40°C，0≤p≤1000bar，覆盖了全球所有海域。该模型相对比较复杂，计算量大，但计算精度较高，主要用于科学研究。本文采用了该精密公式计算海水声速。

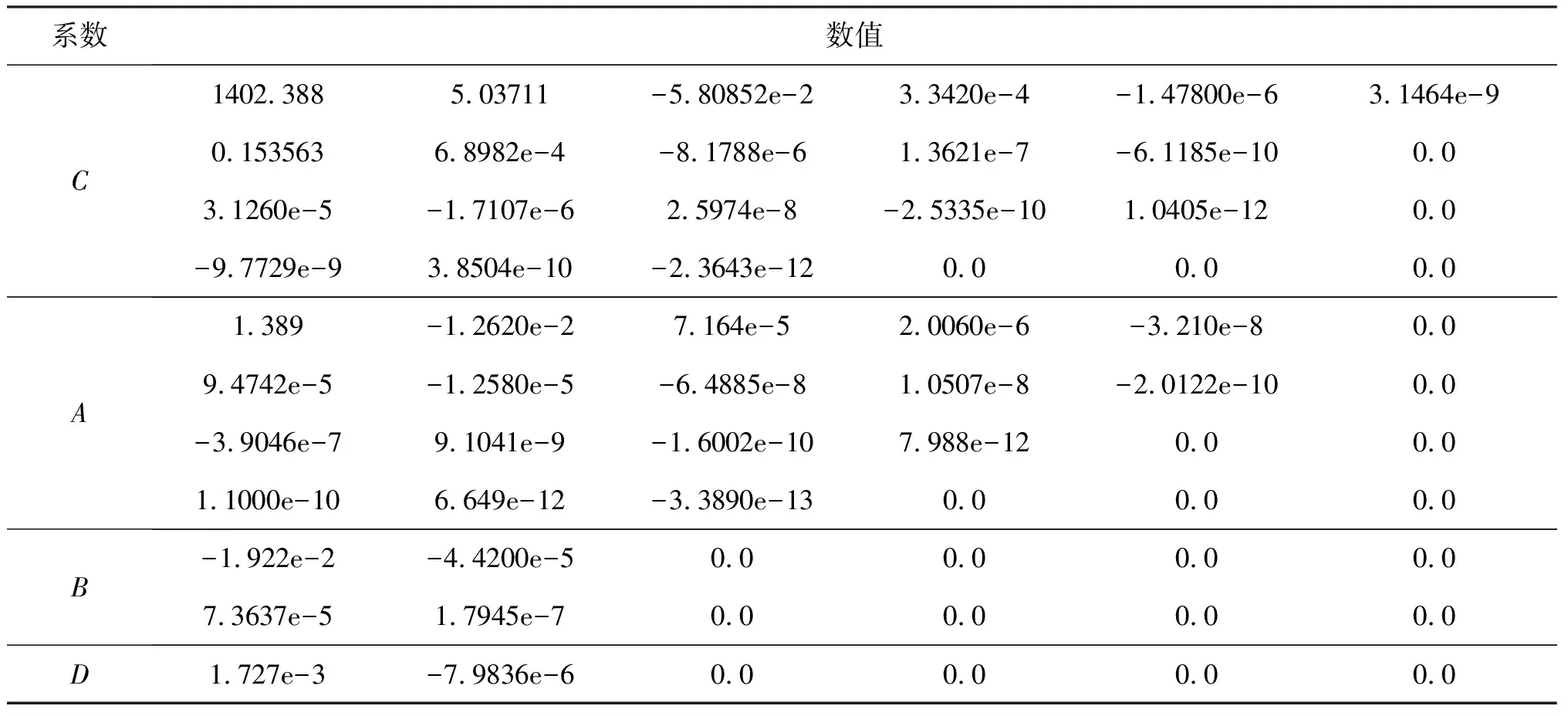
表1 Chen和Millero声速模型的系数

3 由ARGO剖面数据获取海水声速垂直梯度

3.1 ARGO剖面数据

ARGO(the Array for Real-time Geostrophic Oceanography)是一个以剖面浮标为手段的海洋观测系统，其所取得的数据供全世界各国使用。该计划设想用3年～5年的时间，在全球大洋中每隔300km布放一个卫星跟踪浮标，总计为3000个，组成一个庞大的ARGO全球海洋观测网(图1)[7]。

“ARGO浮标”是一种称为自律式的拉格朗日环流剖面观测浮标。当浮标被布放在海洋中的某个区域后，会自动潜入2 000m深处或设定深度的等密度层上，随深层海流保持中性漂浮，到达预定时间(10天～14天)后，又会自动上浮，并在上升过程中利用自身携带的各种传感器进行连续剖面测量。当浮标到达海面后，搜索数据传输卫星，实现自身定位，并通过数据传输卫星系统自动将测量数据传送到卫星地面接收站。浮标在海面的停留时间需约6h～12h，当全部测量数据传输完毕后，浮标会再次自动下沉到预定深度，重新开始下一个循环过程。

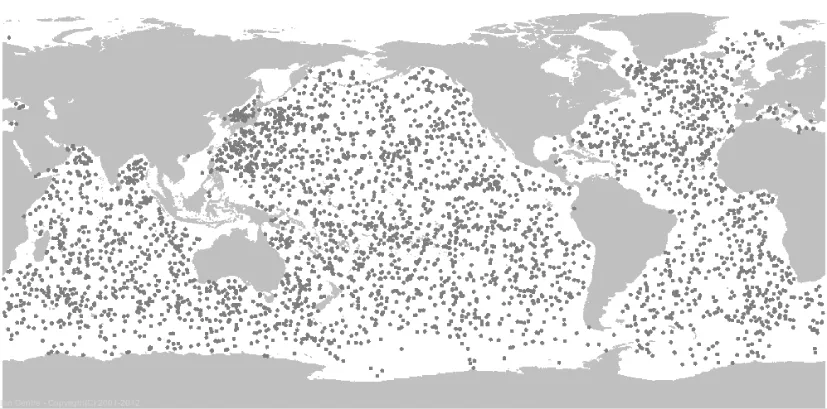
图1 ARGO浮标的全球分布

3.2 多项式拟合ARGO剖面数据

由于ARGO浮标给出的剖面数据是离散的观测数据，该数据是特定位置上的压力和温度、盐度传感器的联合观测值，由于海流等因素的影响，该观测值是深度方向上的非标准的观测值。在进行全球性的数据分析时，需要得到统一的温盐观测量，同时还需要对观测序列中的错误数据进行剔除。本文采用了多项式拟合ARGO浮标的温度、盐度对深度的函数。

温度、深度多项式：

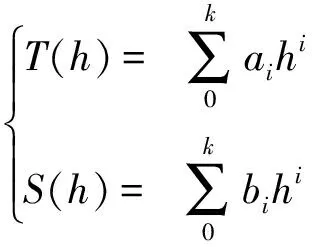
(8)

其中，T(h)为温度深度函数，S(h)为盐度深度函数，h为归一化的深度数值。由于ARGO浮标通常设计的下潜最大深度为2000m，所以，定义：

(9)

根据剖面观测数据，通过最小二乘求解得到拟合多项式的系数。

3.3 ARGO数据的补充

由于ARGO浮标设计的最大深度为2000m，所以ARGO浮标的剖面数据反映上层海水温盐信息，同时，由于表层海水的某些随机性干扰，ARGO剖面数据中常常会出现一些粗差量。另一方面，有些ARGO浮标的观测数据不能够达到2000m，缺少深层海水的信息。因此，在进行数据拟合时，需要将深海稳定的海水信息加入到拟合的模型中，这样实现温度、盐度的深度梯度能够全球统一。

对于深海内部温度统计结果显示，在1000m深处，海水温度为4℃～5℃；在2000m深处，水温为2℃～3℃；3000m深处，水温为l℃～2℃[16]。该信息可以作为ARGO浮标温度拟合的补充观测量。

海水的盐度垂直变化比较复杂。亚热带高盐区从海面一直可延伸到800m～1000m深度。在南北纬40°～50°以外的高纬区，从盐度较低的表层水向下盐度渐增，从1500m～2000m以下盐度几乎不随深度而变化，大约为34.6‰。该信息同样作为ARGO浮标盐度-深度函数拟合的补充观测量，可以很好改善拟合的准确性。

3.4 海水声速梯度

声速随海洋深度增加，呈现洋海内部的声速正梯度(声速随深度增加)变化。在表面等温层和深海等温层之间，存在一个声速变化的过渡区域，这一过渡区域主要呈现温度随深度下降的趋势，称为主跃变层，因而形成典型深海声速剖面图。除高纬度、赤道等特殊区域外，深海的典型“三层结构”是符合海洋结构实际情况的。由于温度、盐度和压力都可以表示为海水深度的函数，因此通过声速度经验映射函数，海水声速对深度映射函数为：

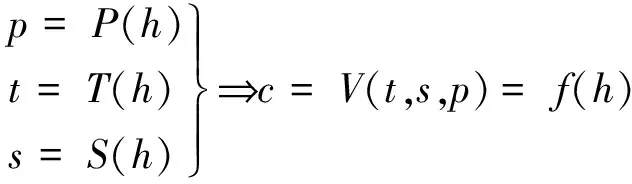
(10)

其中，P(h)为压力深度函数，T(h)为温度深度函数，S(h)为盐度深度函数，f(h)为声速深度函数。同样，采用多项式(式(11))拟合声速深度函数：

(11)

浅海声速剖面分布受到影响的因素更多，但仍有明显的季节待征。在冬季，海水声速梯度大多属于等温层型的声速剖面；夏季则为负跃变层声速梯度剖面。

4 面球谐函数表示声速场

数学理论已经证明，任意定义在单位球面上的平方可积函数或者f(θ,λ)，都可以展开为面球谐函数[17]：

(12)

其中，θ,λ分别为余纬和经度，Pnm(cosθ)为伴随Legendre多项式，anm，bnm分别为规格化后的球谐展开系数。

需要说明的是，海水声速是否能够用球谐函数模型表示。海水声速是海水的一个固有特性，要直接使用面球谐函数展开表示全球海水声速模型，就必须要求海水声速本身在球面上具有可积特性。由于声速可以近似表示为温度、盐度和压力的函数，而温度、盐度和压力在球面上可积，则可以近似认为声速在球面上可积。另一方面，地球是一个近似椭球，海洋占据地球的大部分表面，选择一个球面模型来表示地球的某些特性是最直观和最准确的。

由于直接从数学上证明海水声速在球面上可积很困难，所以，本文采用了数学拟合的方法，将海水声速表示为一个通过球谐函数展开的函数模型，因此，只能通过最小二乘来估计面球谐函数的系数，而不能通过积分计算面球谐函数的系数。

根据该球面上的声速观测数据，得到误差方程[18]：

V=AX-f

(13)

其中，A为正则化后的球面位置函数

构成的矩阵，X为正则化系数，f为误差常数项，V为观测残差。通过最小二乘求解得到声速面球谐函数展开的系数：

X=(ATPA)-1ATf

(14)

拟合精度：

(15)

通过声速垂直梯度可以分析声速在海洋垂直方向上的特性，通过面球谐函数模型可以分析声速在球面上的特性。因此，在不同的深度上，分别求解不同的面球谐函数的声速模型，就可以得到全球三维声速布场。

5 试验和验证

为了验证本文的方法，作者开发了专门用于处理ARGO浮标数据的数据处理软件——Intelligent ARGO(图2)。本文的所有结果都是该软件的直接计算结果和截图。

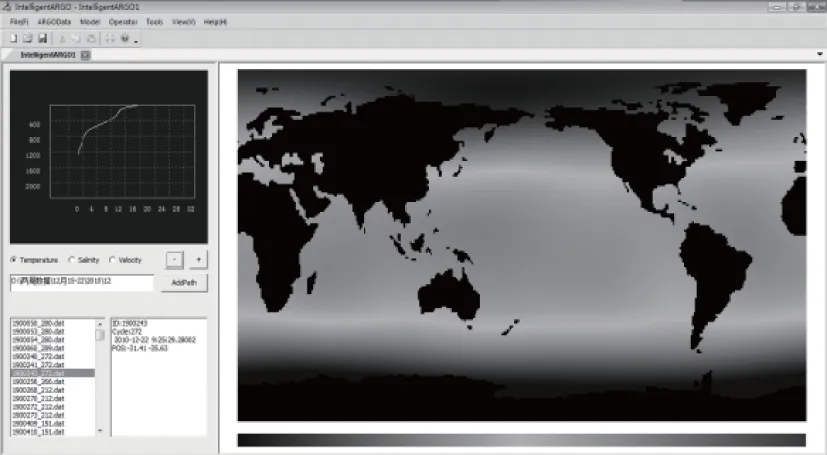
图2 Intelligent ARGO的软件界面

从ARGO数据中心下载了2010年12月15日～17日一周的全球ARGO浮标的温盐剖面数据，一共包括2390个剖面数据文件。对每一个剖面文件先进行压力和深度变换、温盐的曲线拟合、计算标准的温度与盐度层析数据。然后，通过温度、盐度和压力的映射公式计算声速，并得到声速拟合曲线。最后通过球谐函数拟合，获得全球的声速场模型。

5.1 温度盐度拟合

选取ID为1900649的一个ARGO浮标的剖面数据进行温度、盐度地拟合、该浮标是美国布放的一个ARGO浮标，剖面数据的位置是南纬50.097°，东经119.046°。剖面测量采用的是上升过程测量，时间为2010年10月20日。

分别对温度和盐度进行数据拟合，拟合多项式采用了八阶切比雪夫多项式。图3(a)、图3(b)分别是温度和盐度的观测数据和拟合结果。同时，根据温度与盐度和压力采用2.2中的模型计算海水声速，并对海水声速进行拟合，图3(c)为海水声速度拟合结果。

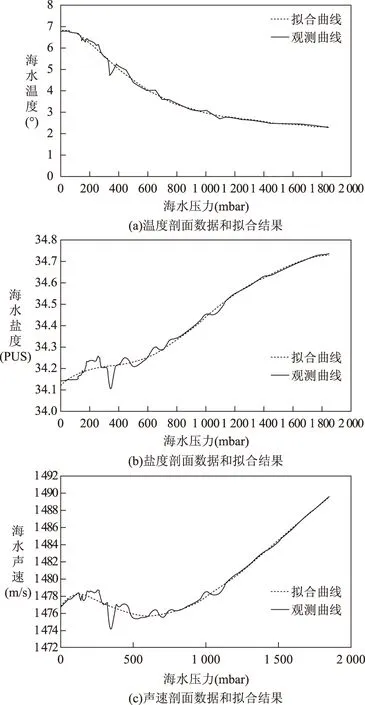
图3 ARGO浮标剖面数据和拟合结果

拟合结果显示，深度小于400m的表层海水由于存在海水热对流等若干的不定因素影响，无论是海水的温度还是盐度，都表现出一定的不规则的深度梯度变化特性，但又不具有完全的随机变化特性。另一方面，由于声速和温度、盐度的函数关系，海水温度、盐度的这种跃层变化，就决定了海水声速也会具有这种无规律的深度梯度特性。

5.2 全球海水声速场

利用覆盖全球的2390个剖面数据，分别拟合得到温度和盐度的深度函数，通过声速度映射公式计算深度分别为5m、100m、200m、300m、400m、600m、800m、1300m、1800m的声速观测数据分布。采用八阶球谐函数模型进行全球声速场的拟合，并根据拟合的全球模型计算得到全球声速场的分布，图4分别是不同深度的全球声速场的分布。

图4 不同深度的全球声速场的分布

通过对全球海水声速场的结果的分析，可以说明：

(1)表层海水声速的水平梯度分布主要决定于太阳的辐射。表层海水声速场存在明显的南北方向梯度变化，而在东西方向上的变化非常小，几乎是平行纬度线(图3(a))。这种变化正好与地球表面温度随纬度的分布相同，而决定这种分布的就是太阳的辐射。同时，在太平洋、大西洋和印度洋都存在一个海水声速度相对较高度区域，该区域也基本上和赤道暖流相吻合。目前，NOAA发布实时的全球海水表面温度格网数据SST，图1显示的结果与NOAA发布的表面SST吻合的很好，也说明海水表面声速场的分布最主要的影响因素是海水的温度。

(2)400m深度以内，随着深度的增加，海水声速变化非常显著。由于400m以内表层风海流、温度对流都比较明显，声速场的变化在一定程度上能够反映海水的这种变化。图3(b)、图3(c)、图3(d)可以明显反映阿拉斯加寒流和秘鲁寒流对东太平洋赤道区域的影响。图3(e)、图3(f)说明，这两股寒流动影响的深度最大也只到600m。但大西洋和地中海区域存在一个深水高温区，因此声速场在此区域存在一个加大的梯度分布。

(3)全球海水声速最小值大部分分布在水下800m～1300m的范围内。海水声速不仅跟温度有关，还跟海水的压力有关，随着深度的增加，海水温度的降低逐渐变小，而海水压力的增大是海水声速变化的主要因素。图3(g)、图3(h)、图3(i)反映了海水声速随深度的增加而显著增加。由于深层海水的温度和盐度都相对比较稳定，在同样深度海水压力作用下，海水声速场的水平梯度变化就不是很明显。

6 结束语

ARGO浮标的剖面数据包含了海水的温度、盐度信息，同时，ARGO浮标的位置变化也反映了洋流的流向和大小。目前，全球的ARGO浮标数量已经超过了3000多个，已经可以获得非常全面的海洋上层的温盐层析数据。基于八阶的Chebyshev多项式表示的海水深度梯度函数、盐度深度函数和声速深度函数可以很好地反映海水的整体垂直特性，同时又具有函数可积分性。另外，采用面球谐函数展开的方式表示全球模型，能够很好地得到该模型的各种频率成分的大小，而且进行全球的分析也非常方便。

参考文献：

[1] 刘伯胜，雷家煜.水声学原理[M].哈尔滨：哈尔滨工程大学出版社，1993：5-10.

[2] 蔡志明(译).水声建模与仿真[M].北京：电子工业出版社，2005：120-143.

[3] 蔡艳辉.差分GPS水下定位系统集成关键技术研究[D].阜新：辽宁工程技术大学，2007：31-45.

[4] DEL G V A.New equation for the speed of sound in natural waters(with comparisons to other equations)[J].Acoust.Soc.Am，1974，56：1084-1091.

[5] FRYE H W，PAUL J D V A.New equation for the speed of sound in seawater[J].Acoust.Soc.Am，1974，50：384-386.

[6] FOFONOFF N P，MILLARD R C.Algorithms for computation of fundamental properties of seawater[D].Unesco Technical Papers in Marine Science，1983：46-50.

[7] Argo part of the integrated global observation strategy[DB/OL].http：//www.argo.ucsd.edu/About_Argo.html.

[8] RICHARD W R，THOMAS M S.Improved global sea surface temperature analyses using optimum interpolation[J].Journal of Climate，1994，7(3)：929-947.

[9] RICHARD W R.A real-time sea surface temperature analysis[J].Journal of Climate，1988，11(1)：75-86.

[10] REYNOLDS R W，RAYNER N A，SMITH T M，et al.An imporved in situ and satellite SST analysis for climate[J].Journal of Climate，2002，15 (4)：1609-1625.

[11] 王桂华，刘增宏，许建平.利用Argo资料重构太平洋三维温盐场和流场[C].Argo应用研究论文集，2006：16-26.

[12] JAMSHIDI S，ABU B.An analysis on sound speed in seawater using CTD data[J].Journal of Applied Sciences，2010，10(2)：132-138.

[13] MAX Y，DENIS A K.Approximation for the inverse speed of sound in seawater，suitable for assimilating acoustic tomography data into numerical models[J].Journal of Atmospheric and Oceanic Technology，2002，19 (3)：1469-1473.

[14] BRIAN D D，PETER F W，BRUCE D C.On equations for the speed of sound in seawater[J].Acoust.Soc.Am，1993，93(1)：255-275.

[15] 国家质量技术监督局.GB 12327-1998 海道测量规范[S].北京：中国标准出版社：1998.

[16] 曾一非.海洋工程环境[M].上海：上海交通大学出版社，2007：40-56.

[17] 梁昆淼.数学物理方法[M].北京：高等教育出版社，2003.

[18] 武汉测绘科技大学测量平差教研室.测量平差基础[M].北京：测绘出版社，1978.