矢量多边形栅格化算法快速并行化方法研究

陈振杰，周琛，李飞雪，李满春，任沂斌

(南京大学 江苏省地理信息技术重点实验室，南京 210023)

1 引 言

矢量数据和栅格数据是地理信息系统(GIS)两种基本的地理数据模型[1]。栅格数据更适合进行空间分析和空间模拟，在遥感地学分析、空间决策分析等领域被广泛应用[2-3]。在大区域地理计算中，经常需要将矢量多边形数据转换为栅格数据。目前，已有不少多边形栅格化方法的研究，形成了内部点扩散法、复数积分法、包含检验法、扫描线算法和边界代数法[4-6]等算法。然而，现有算法大都是串行算法，栅格化效率提升面临瓶颈，难以满足海量矢量多边形快速栅格化的需求[7-8]。

随着并行计算技术的快速发展及并行硬件的门槛不断降低，研发栅格化并行算法成为解决海量数据快速栅格化的有效途径，一些学者开始研究单个矢量多边形栅格化算法的并行实现。Healey等人设计了一种矢量数据向栅格数据转换的并行算法，并给出矢量栅格化并行算法的选择标准[9]；Wang设计并实现了一种基于扫描线法的矢量栅格化并行算法[10]。但将逐一改造现有串行算法不仅工作量大，且效率不高。

本文将在分析典型多边形栅格化算法的基础上，研究串行算法并行化思路，提出一种多边形栅格化算法并行框架，以期解决矢量多边形栅格化算法快速并行化的问题。

2 栅格化算法特征分析

多边形栅格化一般过程可归纳为：逐个遍历所有多边形，判定每个多边形内部及边界上的栅格单元，将多边形属性值赋给这些栅格单元。典型的多边形栅格化算法有内部点扩散法、复数积分法、包含检验法、扫描线算法和边界代数法等。内部点扩散法通过重复设定种子点，填充位于多边形内部及边界上的种子点栅格，直至多边形内部区域被填满(图1(a))；复数积分法与包含检验法类似，都对每个栅格单元，逐个判定其是否包含在多边形之内，并将多边形内部的栅格单元进行填充(图1(b)、图1(c))；扫描线算法通过逐行扫描，识别多边形内部栅格像元条带，并用多边形的属性值将其填充(图1(d))；边界代数法是一种基于积分思想的栅格化方法，通过简单的加减代数运算将多边形属性值赋给多边形内部及边界上的栅格单元，实现多边形的栅格化(图1(e))。

上述栅格化算法虽然实现原理不同，但具有一些共性：①判定多边形内部及边界上的栅格单元是多边形栅格化的关键步骤；②多边形遍历不依赖于具体算法；③单个多边形栅格化的处理都在多边形最小外包矩形内。

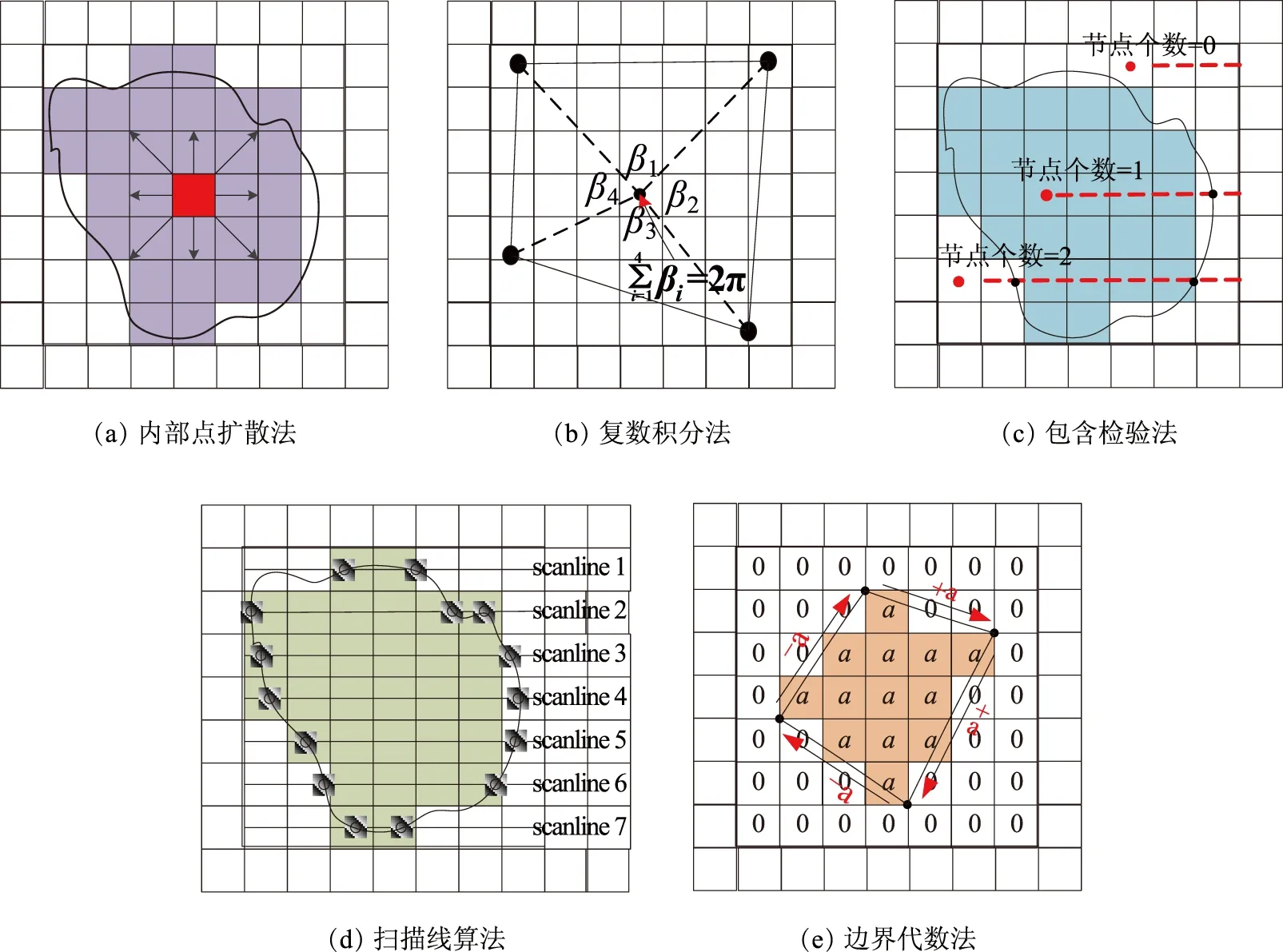
图1 矢量数据栅格化算法基本原理示意图

3 栅格化串行算法并行化方法

3.1 串行算法并行化思路

将串行算法并行化，需要考虑采用何种并行模式、如何将问题域分解。此外，为了能便于将多种栅格化串行算法并行化，需要考虑如何将串行算法的核心功能(或多边形栅格化基本算子)嵌入进来。在分析矢量多边形数据特点和多边形栅格化算法特征的基础上，设计了一种通用的并行框架。该并行框架主要包括：双层并行模式、矢量多边形划分方法、多边形栅格化基本算子调用接口。其中，双层并行模式是实现算法并行的基础和核心，通过充分发挥进程级并行与线程级并行的各自优势，确保尽可能提升算法的并行效率；矢量多边形划分方法是问题域划分的重点，通过对多边形数据进行合理划分，实现各进程之间的任务负载均衡；算法调用接口确保栅格化串行算法能直接嵌入并行框架中，以实现串行算法的快速并行化。

3.2 双层并行模式

在多边形栅格化过程中，利用进程级并行可实现算法的全局并行，但在各进程内部仍是串行处理各个多边形。可见，栅格化填充部分在利用进程级并行后仍具有较大并行潜力。线程级并行由于其共享存储等特点，可以弥补该不足，从而实现对进程内处理过程的加速[11-12]。

本文将MPI和OpenMP相结合，设计了一种进程级和线程级双层并行模式(图2)。在该并行模式中，MPI进程负责读写数据，并对源矢量多边形数据进行划分；OpenMP线程在各进程内部发挥作用，通过循环获取各多边形及其外包矩形区域的栅格单元，并对各多边形调用多边形栅格化基本算子，完成对多边形区域的栅格化。具体过程如图2所示，由2个计算节点中的4个MPI进程分别读取相应的矢量多边形，进而在各进程内部分别派生出2个OpenMP线程，并将多边形分发给多线程并行处理；每个OpenMP线程同时处理1个多边形，通过调用多边形栅格化基本算子完成栅格化处理；当多边形处理结束后，由各MPI进程将栅格化后的结果写入目标栅格文件。

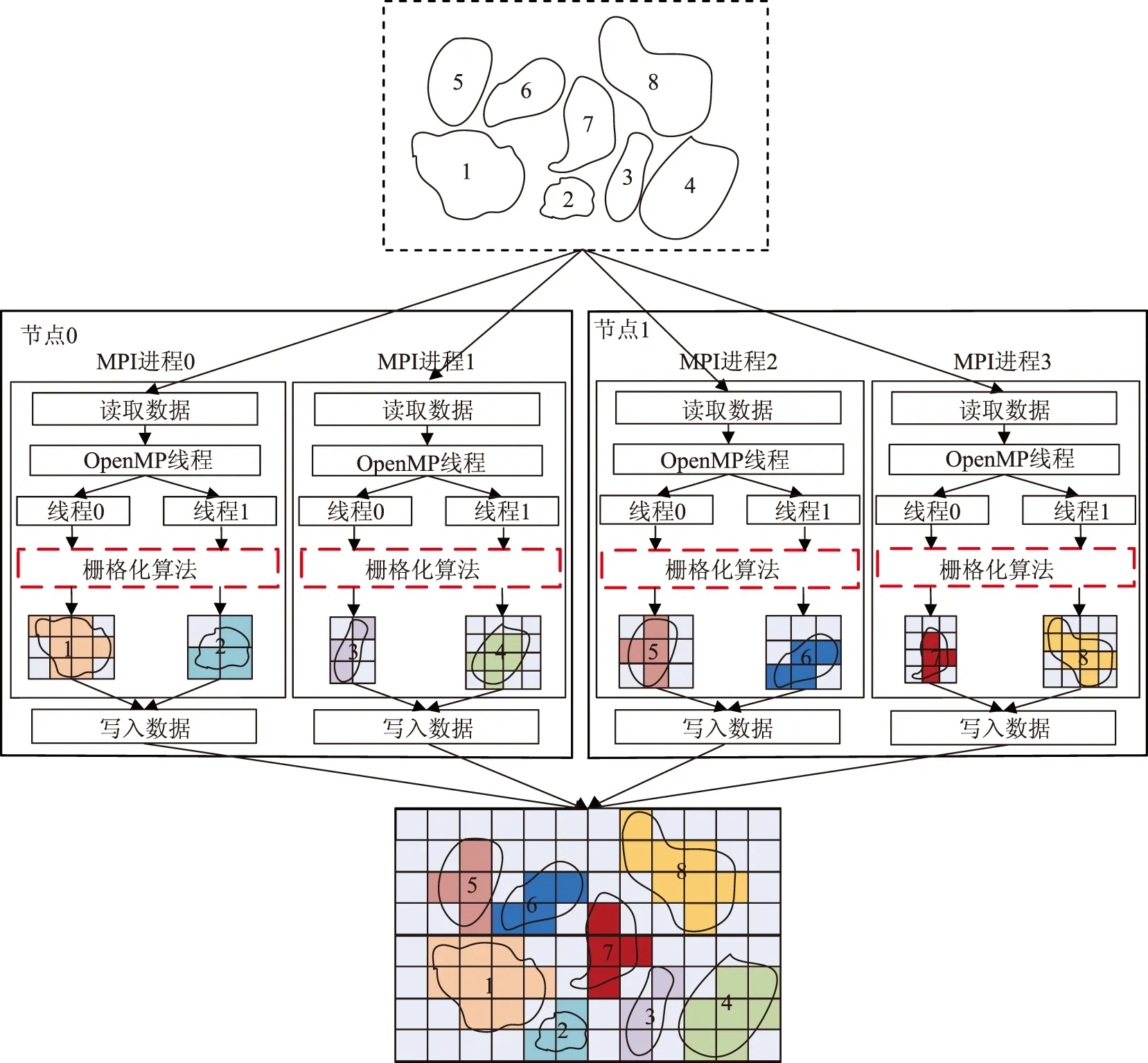
图2 多边形栅格化双层并行模式示意图

3.3 顾及负载均衡的矢量多边形划分方法

针对栅格化双层并行模式，本文设计了一种顾及负载均衡的划分方法，利用多边形包含顶点数评估多边形计算复杂度，并根据进程数目进行均匀划分(图3)。具体过程如下：

①多边形复杂度排序。复杂度指标的选择应兼顾代表性和计算简便。在栅格化过程中，顶点数影响栅格化过程中判定与计算的时间。因此，本文将顶点数作为衡量多边形复杂度的指标，顶点数越多，则认为多边形复杂度越高。通过统计各多边形的顶点数，将多边形按复杂度由大到小排序，形成待处理多边形队列。

②进程间多边形划分。根据多边形复杂度、进程数目求得各进程处理顶点个数Vprocess，顺序从待处理多边形队列中取出多边形归入各进程数据队列中，使得各进程数据队列中的多边形顶点数之和不超过Vprocess，使各进程待处理的多边形复杂度基本相当。其中，Vprocess的计算方法如下：

Vprocess=∑Vi/nProcess

(1)

其中，i为多边形编号，Vi为第i个多边形的顶点数，nProcess为进程数目。

③线程间多边形动态分配。在各MPI进程内部，动态地将待处理的多边形分配各OpenMP线程。各进程数据每次只分配给各线程1个待处理多边形，并标识已分配的多边形；当某个线程处理完后，再从进程数据队列取出1个多边形分配给该线程，直至所有待处理多边形被处理。这样，即使进程数据队列中的多边形复杂度有较大差异，也可确保线程间的负载均衡。

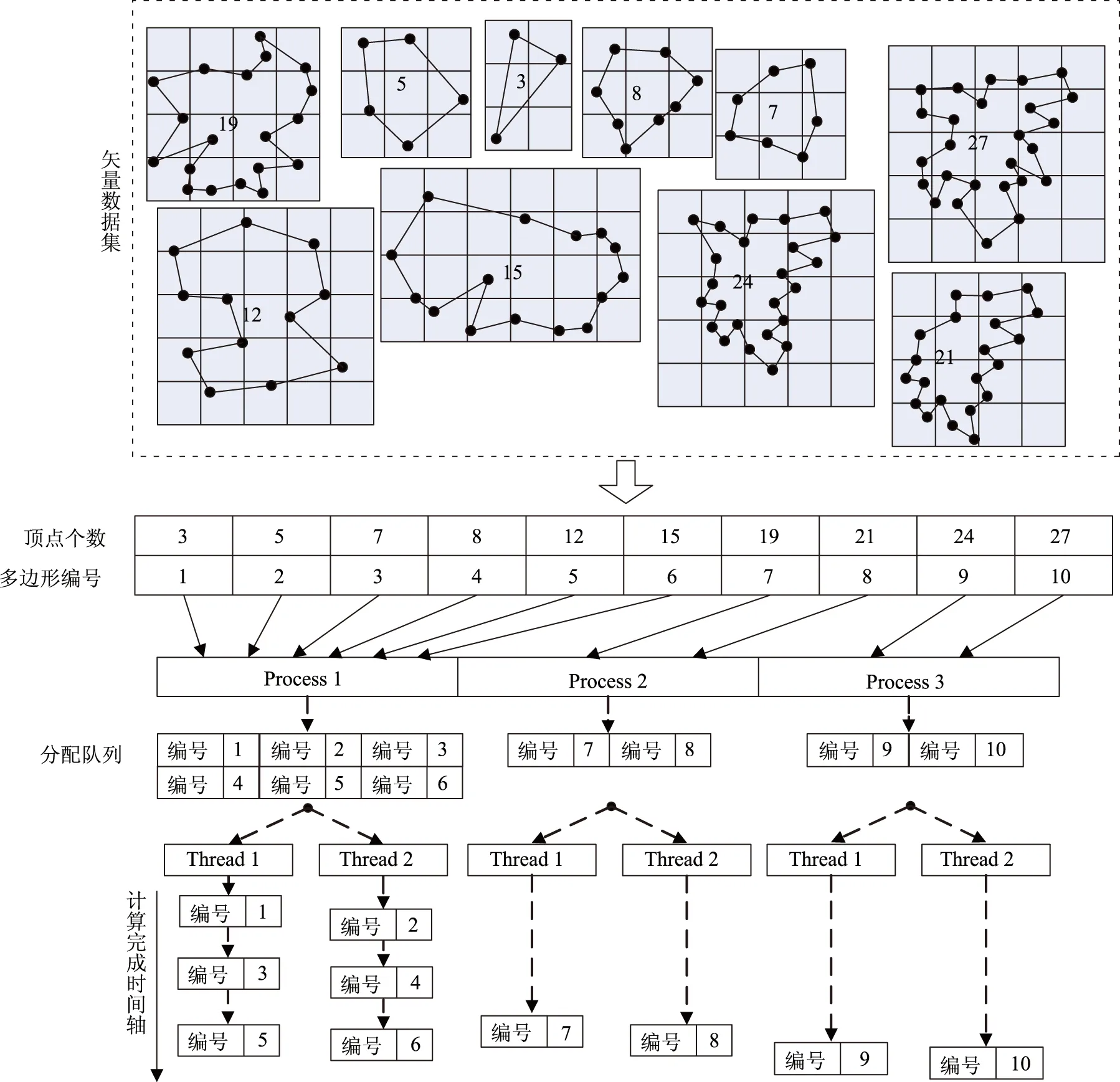
图3 矢量多边形划分方法示意图

3.4 多边形栅格化基本算子调用接口

多边形栅格化基本算子用于实现单个多边形的栅格化，在多边形栅格化过程中被反复调用，是多边形栅格化的核心和基本功能单元。为确保不同的多边形栅格化基本算子能直接嵌入到并行框架中，必须规范多边形栅格化基本算子的调用接口。多边形栅格化基本算子内部以串行方式执行，通过被并行框架调用，实现串行算法的并行化。因此，多边形栅格化基本算子可直接从现有的多边形栅格化串行算法中提取。

通过对常见多边形栅格化算法参数的分析，设计了多边形栅格化填充函数接口参数。参数包括：①多边形顶点信息：将顶点X坐标值与Y坐标值分开存储，分别用double*padfX、double*padfY表示。②多边形属性值：用double*pValue表示。③目标栅格数据：用char*pCBData表示，用于临时存储多边形外包矩形内的目标栅格数据，栅格化后函数返回更新后的目标栅格数据pCBData。任何多边形栅格化填充算法，只要满足上述接口规范的要求，且程序开发语言相同，就可直接嵌入到并行框架中，实现算法的并行化。

4 测试结果与分析

4.1 测试环境与测试数据

测试环境为浪潮Linux高性能集群。集群包含4个节点，每个节点包含2颗四核八线程Intel Xeon CPU、12GB内存、292GB硬盘、千兆以太网卡。软件配置为Centos Linux 6.0操作系统、Openmpi 1.4.1、OpenMP 2.0、PostGIS 2.0.3+PostgreSQL 9.0.5数据库。

测试数据为某省土地现状地类图斑数据。数据格式为PostGIS格式，数据空间参考系为1980西安坐标系，图斑总数为1186万个，数据量为5.5GB。数据共有4个类别，分别以分类1、分类2、分类3和分类4表示。原始试验区的矢量多边形如图4所示。

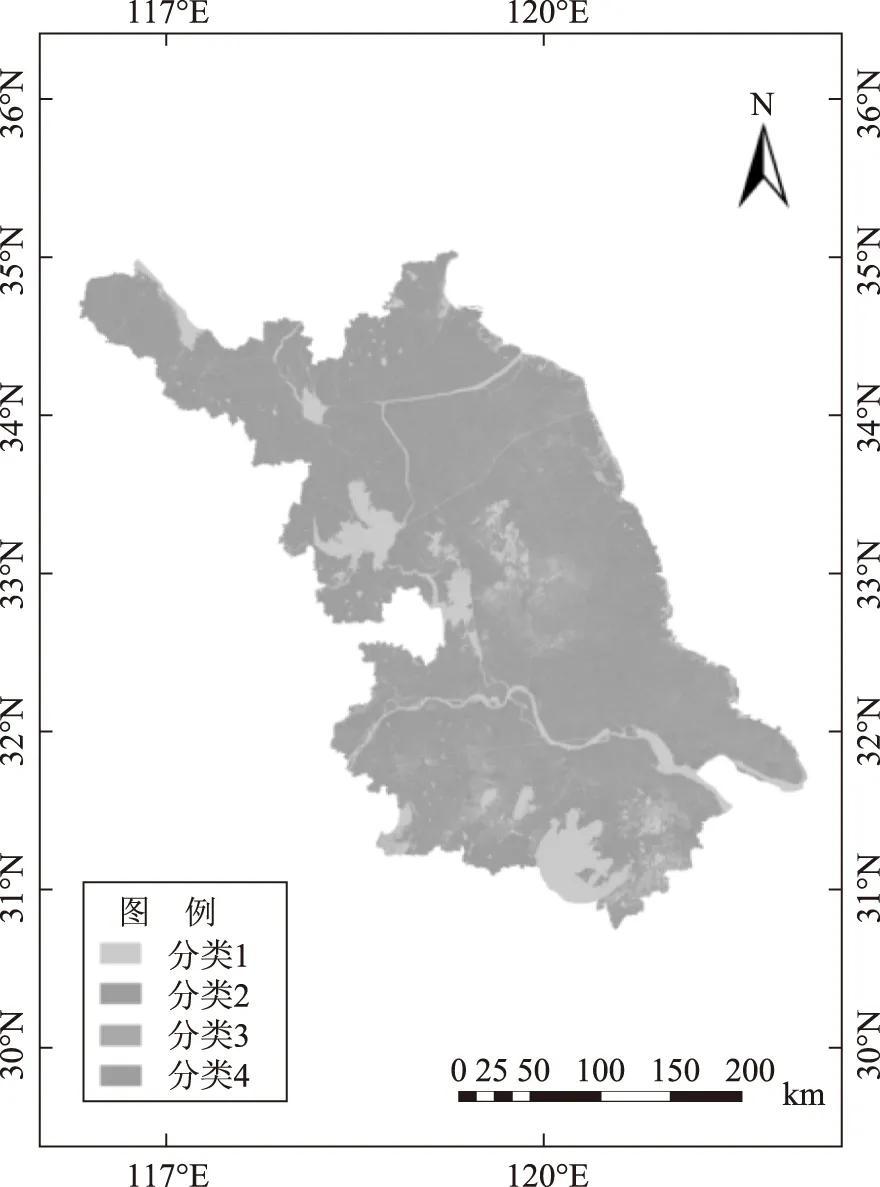
图4 矢量多边形测试数据示意图

本文选取扫描线算法和边界代数法两种常用多边形栅格化算法作为算法用例，利用本文形成的并行框架将扫描线与边界代数串行算法快速并行化。试验设定输出栅格单元大小为20m×20m，输出的栅格数据大小为25880×24225。试验结果表明，经并行化后的扫描线并行算法与边界代数并行算法均运行稳定，且结果正确。

4.2 并行效率分析

运行时间和加速比是度量算法并行效率的重要指标。其中，算法的运行时间是从算法启动直至最后1个进程执行完所花费的时间；加速比是同一个任务在串行及并行环境下运行时间的比值[13]。通过测试本文实现的不同并行算法的运行时间和加速比，比较并行算法较于串行算法的性能提升和不同算法并行效率的差异。其中，并行算法计算单元数目用NP×NT数表示，NP表示并行算法使用的MPI进程个数，NT表示OpenMP线程个数。对于同一NP×NT数，常有不同的进程与线程组合，本文测试采用取得最佳效率的组合来表示。测试结果如图5所示。图5(a)、图5(b)为不同并行算法与串行算法的对比结果。从中可看出，利用本文的并行化方法改造后的多边形栅格化算法大大减少了栅格化时间，取得了良好的加速比，从而验证了本文设计的并行化方法的有效性。图5(c)、图5(d)为两种并行算法的效率对比结果。结果表明，边界代数法较扫描线算法更为快速地实现栅格化转换，取得更好的并行效率。原因在于边界代数法以整个栅格单元为基本操作单位，从而实现对栅格矩阵的直接操作；扫描线算法则需要进行扫描线与多边形交点的多次判别，因而效率低于边界代数法。

4.3 不同并行模式对比

本文并行算法采用双层并行模式实现，为比较其与常规方法的效率差异，本文实现了基于MPI并行模式的栅格化算法，并将两种并行模式进行了效率对比，测试结果如图6所示。从图中可明显地看出，对于每一种算法，双层并行模式效率均优于MPI并行模式。对于MPI并行模式，当进程数超过32时运行时间缓慢回升；但对于双层并行模式，随着NP×NT数的增大，运行时间一直降低，直至达到64。原因在于本文实验集群共包含32个使用超线程技术的计算核心，对于MPI并行模式，可用计算单元数为32；对于双层并行模式，可用计算单元数为64。可见本研究所选的双层并行模式可以更好地利用系统资源，能获得更好的并行效率。

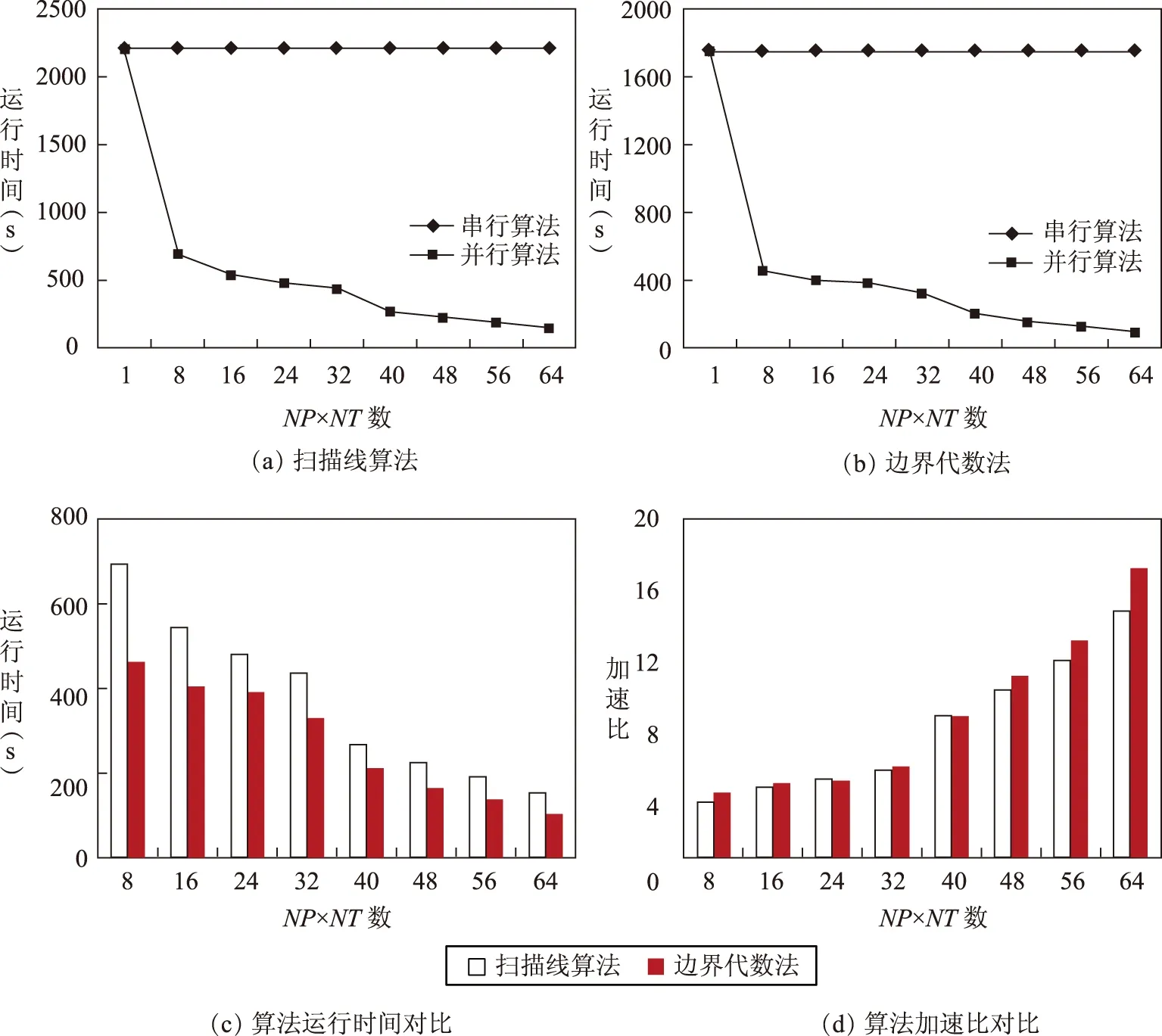
图5 并行算法效率测试结果

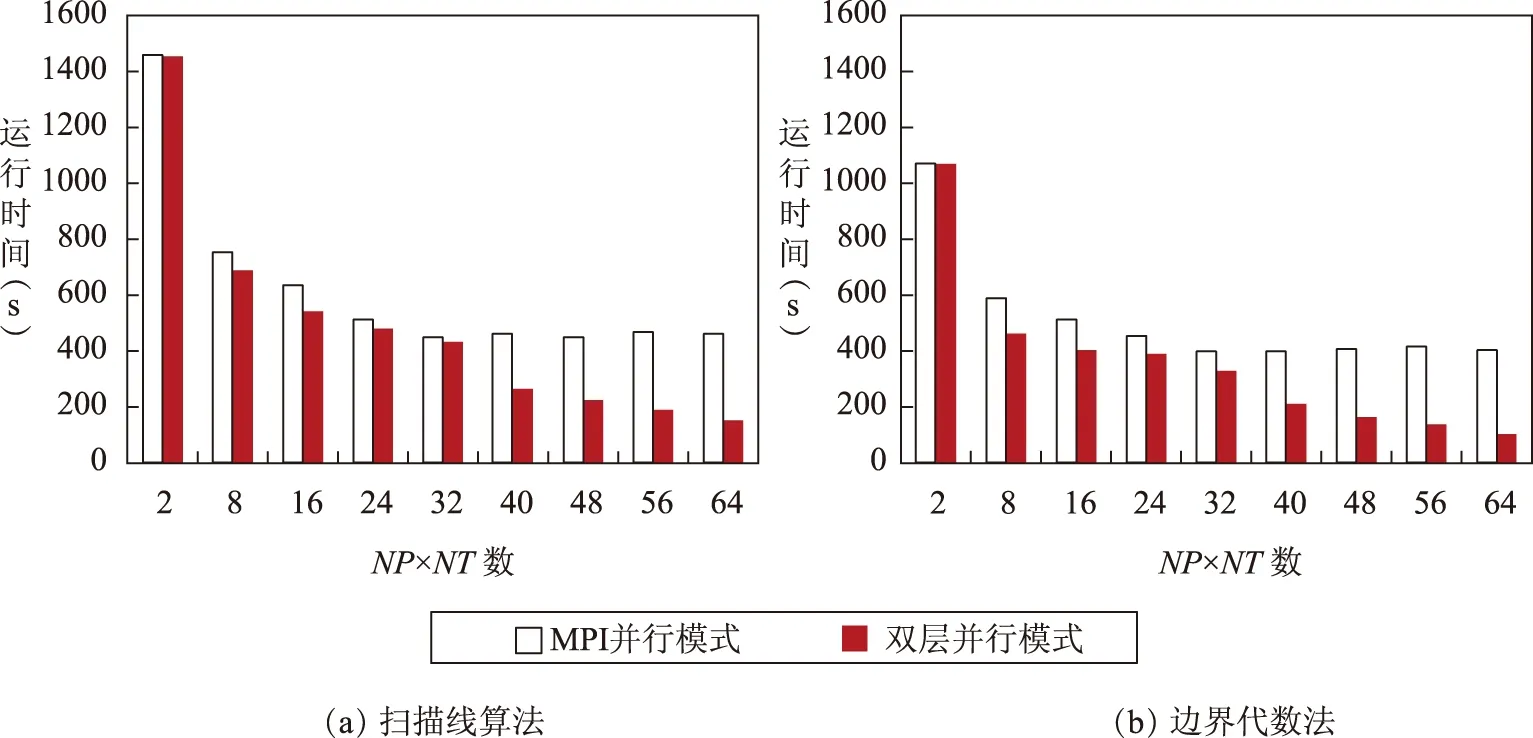
图6 算法并行模式效率对比结果

5 结束语

本文在分析典型多边形栅格化算法的基础上，提出多边形栅格化算法并行框架，从而形成了一种多边形栅格化串行算法快速并行化的方法，为解决地理计算串行算法快速并行化问题提供有

益的借鉴。试验表明，本文设计并实现的并行化方法可实现栅格化串行算法的快速并行化，利用此方法改造后的算法具有良好的稳定性和加速比。在后续的研究中，将进一步探索该并行框架在其他矢量数据处理中的适用性，并拓展和深化相关研究与应用。

参考文献：

[1] MAGUIRE D J，GOODCHILD M F，WRHIND D.Geographical information systems：Principles and applications[M].England：Longman Scientific and Technical，1991.45-54.

[2] GOODCHILD M F.Scale in GIS：An overview[J].Geomorphology，2011，130(1-2)：5-9.

[3] CONGALTON R G.Exploring and evaluating the consequences of vector-to-raster and raster-to-vector conversion[J].Photogrammetric Engineering and Remote Sensing，1997，63(4)：425-434.

[4] 龚健雅.地理信息系统基础[M].北京：科学出版社，2001：167-169.

[5] 吴立新，史文中.地理信息系统原理与算法[M].北京：科学出版社，2003：202-212.

[6] JIMÉNEZ J J，FEITO F R，SEGURA R J.A new hierarchical triangle-based point-in-polygon data structure[J].Computers and Geosciences，2009，35(9)：1843-1853.

[7] WANG S，ARMSTRONG M P.A quadtree approach to domain decomposition for spatial interpolation in grid computing environments[J].Parallel Computing，2003，29(10)：1481-1504.

[8] GUAN Q，CLARKE K C.A general-purpose parallel raster processing programming library test application using a geographic cellular automata model[J].International Journal of Geographical Information Science，2010，24(5)：695-722.

[9] HEALEY R，DOWERS S，GITTINGS B，et al.Parallel processing algorithms for GIS[M].London：Taylor and Francis，1997.

[10] WANG Y，CHEN Z，CHENG L，et al.Parallel scanline algorithm for rapid rasterization of vector geographic data[J].Computers and Geosciences，2013，59：31-40.

[11] BOVA S W，BRESHEARS C P，CUICCHI C E，et al.Dual-level parallel analysis of harbor wave response using MPI and OpenMP[J].International Journal of High Performance Computing Applications，2000，14(1)：49-64.

[12] JIN H，JESPERSEN D，MEHROTRA P，et al.High performance computing using MPI and OpenMP on multi-core parallel systems[J].Parallel Computing，2011，37(9)：562-575.

[13] XIE J.Implementation and performance optimization of a parallel contour line generation algorithm[J].Computers and Geosciences，2012，49：21-28.