管线保温损失抗扰转换算法研究*
2014-07-31王玲
王 玲
(天津机电职业技术学院,天津 300131)
管线保温损失抗扰转换算法研究*
王 玲
(天津机电职业技术学院,天津 300131)
找到管线表面温度值和热流值的标准化转换模型。利用模拟装置进行实际测量并对现场采集的数据进行处理,得到需要条件下排除干扰的数据。构建系统模型的算法并进行仿真从而验证模型可否达到要求的技术精度。
管线保温;转换模型;数据采集;Matlab软件仿真
0 引 言
石化行业是我国的支柱产业。石化行业生产线长、涉及面广,企业中有大量原油、成品油、天然气等输油输气管道,石化企业的油田、采油厂、炼油厂、化工厂、油库、加油站、输油(气)管线遍及全国城市、乡镇、车站、码头、千家万户。在石化企业现有的中压、高压蒸汽管道中由于保温状况不良,大多数管线热量损失严重,甚至造成管线末端的蒸汽温度无法满足工艺要求,直接影响工业生产,导致企业能源成本增加。
在实际工况中通常依据管线表面热流值对比国家标准来判断管线的保温性能是否达到标准。而在实际测量中发现现场因素(如环境温度、风速)对测得的管线表面热流值影响比较大,整个测试的结果受外界干扰,国家标准给出的评定依据为标准条件(环境温度一定、风速较小)下的值,不能直接用于衡量现场测量值。所以此顶研究要求对现场采集的数据进行处理,得到标准条件下的数据且可以用国家标准进行衡量。从现场实测数据到标准条件下的数据转换是基于一个系统模型模型即实测管线表面温度值和标准条件下热流值之间的转换模型。
结合项目研究的目的和意义,研究中主要开展以下工作。
(1) 结合现场实际情况建立实际管线的模拟装置,模拟工业现场实际测量时的环境情况。
(2) 利用模拟装置进行实际测量,通过检测采集到相关数据,包括:现场环境温度、环境风速、模拟实际管线表面温度和热流值。
(3) 通过对采集数据的分析发现数据量比较大,结合经验公式发现其中有存在明显差异的数据,要将这部分异常数据剔除。
(4) 系统建模方法的分析,研究构建系统模型的算法,根据构建的样本数据对建模算法进行分析验证。用递推最小二乘法建模并进行了仿真,从网络输出的预测误差值分析最小二乘法拟合精度不够,没有达到预期技术要求的10-2的精度等级。
1 数据采集装置
在开展研究的过程中要针对实际工况中的现场在实验室中开展模拟实验,在实验过程采集实验数据以便于后续的神经网络训练,这些数据决定了神经网络系统建模的最终可行性,所以实验装置的设计、安装、测试以及实验数据的采集都是非常重要的。针对这一情况,研制可靠且实用的温度控制系统显得非常重要。温度控制系统是正确完成实验取得实验数据的重要保障,它采用传感器技术、单片机技术和现代通信技术实现自动化管理,具有各种安全保护,运行监控和管理等功能。
所使用的数据采集装置依托传感技术的优势,通过I/O接口板、温度传感器等现代电子产品实现实时采集数据,并以各种通讯协议方式,实现数据传输、处理、实时监控等功能,是进行自动监控的一种智能、高效系统。
整个系统由温度传感器、A/D转换电路、单片机等组成数据采集系统(即下位机)。温度传感器检测温度后,输出信号为4~20非曲直mA电流信号,在经过250 Ω电阻后转变成1~5 V电压信号,进行A/D转换。电压信号经过A/D转换后变成数字信号,传给单片机,再由RS-485总线传给上位机,有上位机进行数据处理及进行相应的显示。其结构图如图1所示。
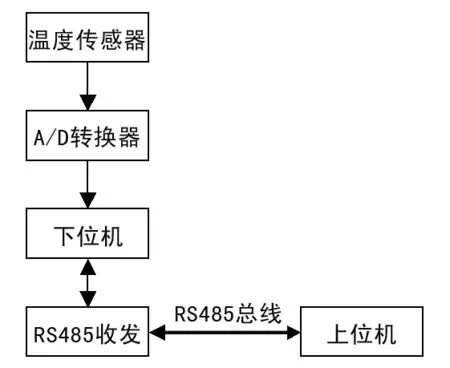
图1 数据采集结构图
2 数据的预处理
试验中选择热流计的三个贴片:贴片1、贴片3、贴片4进行测量,测量的数据结果由显示屏幕显示。其中,CH2和CH31对应贴片1的表面温度和热流值;CH6和CH35对应贴片3的表面温度和热流值;CH8和CH37对应贴片4的表面温度和热流值。采集的数据可以拷贝到热流计的数据卡中,然后导入相应的EXCEL文档以备后续试验使用。因为样本数据数量比较大,需要先对采集的数据进行简单的分析,可能有些数据因为模拟装置的问题本身就是严重偏离真实情况的,对于这些数据要剔除,剩下的数据也要进行分类汇总进行相应的简化,最终取得能都训练神经网络的有效数据。
实验进行过程中,测量间隔时间较短(2 s),这样会得到大量的采集的数据,非常有利于后续用书系统建模,但是仍旧不能简单的就全部用来使用。在这些数据中有些值存在明显的偏差,从数据表面看来就不符合实际,这其中可能有实验装置问题引起的,需要验证并予以选择。筛选后的数据也发现了在不同的时间点,某些表面温度值相同的情况,对于这些温度值相同的数据可以进行汇总,在不影响精确度的情况下减少样本数据,可节省网络训练所需要时间,也避免了网络的过拟合。数据的预处理主要从以下几个方面展开。
(1) 采集的数据的筛选 用热流计的贴片测量出温度和热流值,根据经验公式进行筛选。根据工作人员的实际经验总结出了相应的热流值计算的经验公式。结合公式,总结出通用所有情况时的,根据温度计算热流值的经验公式如下:
Q= [1.37×(T表面-T环境)0.33+3.78×
(T表面-T环境)0.11+6×(v风)]×
(T表面-T环境)
(1)
式中:T表面为贴片所在位置管道表面的温度值;T环境为测量时实验室环境温度;v风为测量时实验室的风速。
(2) 由于热流计测量温度和热流的时候都能侦测到该时刻的最大值和最小值,首先针对每一个时间点的最小(min)和最大(max)求出温度的平均值,同时按照相同的原理求出该温度下对应热流值的最大和最小值的平均,以此作为一组输入输出数据。
(3) 以温度值为标准降序排列。按照降序的规律排列温度值的顺序,同时将对应的热流值也按照温度降序的顺序进行排列。
(4) 分类汇总。把所有温度值相同的值分类汇总,然后求出其对应热流值的平均值,一次为一组对应数据,将这些数据提取出来以供后续训练神经网络使用。
3 递推最小二乘方法 (RLS法)
在建模进行排除干扰的过程中,需要使用一些算法来完成模型建立。对于该研究项目,由于很难找出实际测量值与实验室标准值之间的精确解析关系,所以基于温度转换的内部机理,建立温度转换的解析模型是不可能的。应用所测得输入输出样本数据对进行数值建模分析,建立满足一定精度的温度标准化转换数值模型即基于最小二乘法和人工神经网络的管线表面温度值和热流值的标准化转换模型是解决此问题的一个出路。
考虑CAR模型:
(2)
式中:{y(k)}和{u(k)}为可测的输出和输入,{ε(k)}为不可测的随机干扰。上式还可表示为:
A(z-1)y(k)=B(z-1)u(k)+ε(k)
(3)
其中:
A(z-1)=1+a1z-1+a2z-2+…+anz-n
B(z-1)=b1z-1+b2z-2+…+bnz-n
还可表示为:
y(k)+φTkθ+ε(k)
(4)
其中:
θTk=[a1,a2,……,an,b1,b2,……,bn]
φTk=[-y(k-1),……,-y(k-n),u(k-1),……,
u(k-n)]
当进行了k=1-n,2-n,…,0,1,2,…,N共计(N+n)次采样,得到N个方程:
用矩阵表示:yN=ΦNθ+εN
(5)
其中:yN=[y(1),y(2),…,y(N)]T
4 仿真结果
综合上述建模方法,应用最小二乘算法进行验证。使用模拟装置采集的数据,经过分析处理得到用于训练模型的样本数据,针对这组样本数据结合递推最小二乘法编写MATLAB程序进行仿真,得到以下仿真图形。
图2中黑色实线实测数据的曲线分布,点划线为用最小二乘法拟合后的曲线。从上图中可以看出,拟合曲线和样本数据还是有一定的差距,拟合情况不是很理想。下面再从误差分布上看一下拟合情况,误差曲线如图3所示。
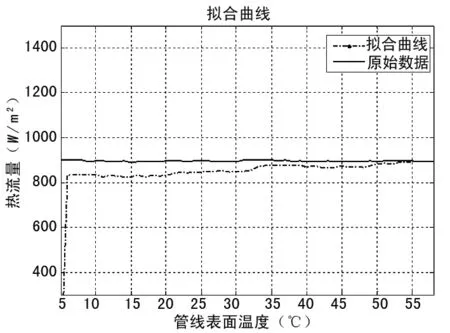
图2 最小二乘曲线拟合
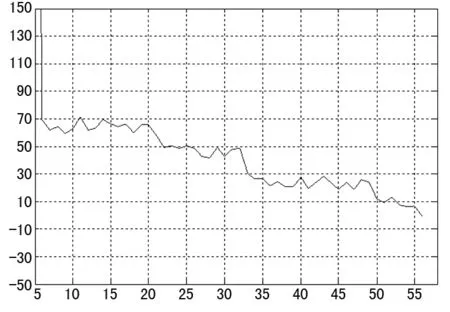
图3 误差分布曲线
从误差分布曲线上可以看出,误差值分布在(-10~70)区间范围内,虽然相对于输出的整体范围(850~900)区间误差值不是很大,但是误差区间也占整体输出区间的8%。如果使用这种算法建立模型,预测误差的精度达到10-1数量级。而项目要求用这种算法得出的模型精度在10-2数量级,使用这种方法很难得到预期要求的模型精度。由于使用最小二乘法建立模型得到的误差没有达到预期要求的精度等级,所以放弃使用这种算法建模。
5 结 语
建立的模型要完成实测数据到标准条件下数据的转换。因为输入量和输出量之间的对应关系很难通过分析过程运动规律得到,而系统的特性必然表现在这些输入输出数据之中,因此可以利用输入输出数据所提供的信息来建立数学模型。
虽然利用递推最小二乘算法可以建立系统模型并完成仿真,但是仿真结果显示出拟合的曲线和实际数据之间有一定的差异。拟合曲线没有精确地描述出实际数据的特性,从误差分布看出预测的精度等级也没有达到项目预期的技术要求,所以这种方法不适合针对采集数据的系统建模。另外,利用最小二乘法建模要预先选定数学模型,而采集的数据未必一定能满足这种模型。如果能够直接利用输入输出数据找到它们之间的映射关系,便可以更轻松的实现系统辨识。综上所述,最终确定依据采集数据利用人工神经网络完成对于系统模型的辨识。
[1] 徐 鹏,葛 斌,殷 戈.蒸汽管网设计建模和优化[J].华东电力,2007,35(3):16-20.
[2] 李 瑜,崔国民,涂惟民,等.蒸汽管网的建模和设计优化[J].节能,2009,10(4):14-17.
[3] 臧荣春,崔平远. 陀螺随机漂移时间序列建模方法研究[J].系统仿真学报, 2005,17 (8):1845-1847.
[4] Kaderli A , Kayhan A S. Spect Ral Estimation of ARMA Processes Using ARMA Cepstum Recursion[J].IEEES ignal Processing Letters,2000,7(9):259-261.
[5] 李志农,何永勇,吴昭同,等. ARMA 模型盲辨识仿真研究及其在机械故障诊断中的应用[J].振动与冲击,2006,25(1):122-126.
[6] Broersen P M T,Waele S D. Automatic Identification of Time Series Models from Long Autoregressive Models[J]. I EEE Trans .on Instrumentation and Measurement,2005,54(5):1862-1868.
Anti-interference Transformation Algorithm Research of Pipeline Insulation Loss
WANG Ling
(TianjinVocationalCollegeofMechanicsandElectricity,Tianjin300131,China)
The main purpose of the study is to find the standardized transformation model of pipe surface temperature and heat flow value. Actual measurement is done by a new simulator,and the data collected on the spot are processed, the data eliminating interference under the needing condition is obtained. The algorithm of system model is built, the requirements of technical accuracy of the model is verified.
pipeline insulation;transformation model;data acquisition;Matlab simulation
2014-01-20
王 玲(1982-),女,天津人,讲师,主要从事自动化,机电一体化方面的科研工作。
TE832
A
1007-4414(2014)02-0109-03
