随机因素作用下的超临界Hopf分岔附近的动力学
2014-07-31李玉叶
李玉叶
(赤峰学院 数学与统计学院, 内蒙古 赤峰024000)
随机因素作用下的超临界Hopf分岔附近的动力学
李玉叶
(赤峰学院 数学与统计学院, 内蒙古 赤峰024000)
本文研究了确定的和随机的INa,p+IK神经元模型中的超临界霍普夫(Hopf)分岔附近的动力学行为,随机模型中靠近Hopf分岔点的随机节律被认为是整数倍节律模式;还研究了相应于分岔点附近的随机自共振机制.结果不仅揭示了超临界Hopf分岔点附近的神经放电的统计特征和动力学机制,还给出了实用于现实神经系统中Hopf分岔的判断指标.
Hopf分岔;随机自共振;神经放电模式;II型兴奋

李玉叶,女,1980年7月生,内蒙古赤峰市人。2004年毕业于内蒙古大学理工学院数学系数理基地(数学),获得理学学士学位;2009年毕业于内蒙古大学数学与统计学院应用数学专业,获得理学硕士学位;2012年毕业于陕西师范大学生命科学学院生物物理专业,获得理学博士学位。
研究方向:非线性动力系统的分岔与混沌理论及其应用,神经动力系统与复杂网络动力学,神经信息传递与编码。
1 引言
整数倍节律模式的放电现象最初是在实验中被发现的.早在1967年,Rose[1]发现猴听神经纤维表现这种较为异常的放电活动模式,但是,这一实验现象很长时间内并未得到合理的解释和引起大家的注意.随后更多的实验发现了类似的现象,如Douglass[2]在选择小龙虾水力敏感触须的机械感受器作为实验对象时,发现其放电节律模式呈现整数倍现象.这种具有“遗漏”现象的放电模式,在外周期刺激下的放电节律和放电尖峰的峰峰间期统计直方图呈现出两个特点:(1)多数峰峰间期是某一放电峰峰间期的整数倍;(2)峰峰间期统计直方图是多模态的高峰状,且随着ISI的增大其出现的频率呈降低的趋势,如图3(b)和(c)所示.
随着随机共振(stochastic resonance)概念被引入神经科学,整数倍节律的现象得到了研究,揭示了噪声在神经信息处理中会起关键的正面作用;同时也揭示了整数倍的特征及动力学机制.在没有外界周期信号激励的情况下,现实生物的自发神经放电也发现了位于静息和周期1节律之间的自发整数倍节律[3];将随机因素引入到确定性模型形成的随机模型模拟了从静息到整数倍放电再到周期1放电的过程[3];而自发整数倍节律也被揭示为是经过随机自共振(Autonomous stochastic resonance or coherence resonance)机制在Hopf分岔点附近产生的,也是现实神经系统中Ⅱ型兴奋的自发放电的真实表现[3].
在本文中,基于实验中神经起步点的整数倍节律[4,5],通过噪声对神经元INa,p+IK模型在超临界Hopf分岔附近的作用,得到由随机共振产生的整数倍节律,并对其产生的节律进行随机共振分析.
2 INa,p+IK模型[6]及特性
此模型是与Morris-Lecar(ML)模型类似的模型,基于来自实验的一个合理的假设:钠的门控变量m(t)比膜电位V快,m(t)即时接近于m∞(V)的值.因此,令m=m∞(V)把三维系统简化成二维系统,确定性INa,p+IK模型方程如下:

其中V是膜电位,I是膜电流,C膜电容,gNa、gK、gL分别是钠电导、钾电导和漏电导,ENa、EK、EL是相应的平衡电位,m∞(V)、n∞(V)分别是Na+离子通道和K+离子通道打开概率的稳态值,它们满足如下方程:

模型中的各个参数的取值分别为:C=1.0;EL=-78.0;gL=8.0;gNa=20.0;gK=10.0;Vm=-20.0;Vn=-45.0;Km=15.0;Kn=5.0;τ(V)=8.0;ENa=60.0;I=3.0;Ek为分岔参数.此时INa,p+IK模型为II兴奋性的.时间单位msec.
引入高斯白噪声ξ(t)作用到方程(1)式,方程(2)式不变,就形成了随机INa,p+IK模型.白噪声ξ(t)具有以下性质:(1)统计平均值为零,<ξ(t)>=0;(2)不同时刻的ξ(t)互不相关,<ξ(t) ξ(t')>=D2δ(t-t'),其中D是噪声强度,δ(·)是Diract-δ函数.
在确定和随机的INa,p+IK模型中,在数值模拟中,我们采用定步长Mannella算法[7]对微分方程组进行积分,其积分步长取0.001msec.
确定性INa,p+IK模型关于参数Ek的平衡点分岔图,如图1所示.当Ek<-88.216156系统存在一个稳定的不动点.在Ek=-88.216156发生了超临界的Hopf分岔,有向右的稳定的如图2所示.随着参数Ek的继续增加,Ek=-54.379639发生了亚临界的Hopf分岔,同时有不稳定极限环产生,然后稳定极限环(粗实线)和不稳极限环(粗虚线)相碰发生了极限环的鞍结分岔,极限环消失,这里不予关注.极限环产生(黑实线代表极限环的最大幅值和最小幅值),

图1 确定性INa,p+IK模型关于分岔参数Ek的平衡点分岔图
3随机INa,p+IK模型中的随机放电节律

图2 当不同Ek时,随机INa,p+IK模型整数倍节律模式:(a)和(a1)是膜电位的时间历程图;(b)和(b1)是ISI的时间历程图;(c)和(c1)是ISI的统计直方图;(d)和(d1)是ISI的回归映射图.其中(a)、(b)、(c)、(d)代表Ek=-88.5时,(a1)、(b1)、(c1)、(d1)代表Ek=-88时
在确定性INa,p+IK模型中,Ek=-88.5和Ek=-88时其行为为静息态,无放电.在随机INa,p+IK模型中,在引入合适的噪声强度(D=0.5)时,会有非周期放电节律产生.其放电轨迹如图2(a)和(a1)所示,看似是没有规律的放电活动.其峰峰间期(ISI)序列,都具有明显的分层现象,如图2(b)和(b1)所示.其峰峰间期(ISI)统计分布图标也为多峰态,随着各模态的峰随峰峰间期的增大而逐渐衰减,且大多数峰峰间期大约为第一模态峰峰间期的整数倍,如图2(c)和(c1)所示.所以通过上述分析可以认为此随机节律为整数倍节律,同时可以理解整数倍节律模式的膜电位的时间序列是在周期一与静息交替出现,且静息的长基本是周期一的整数倍;但在Ek=-88.5和Ek=-88时整数倍节律的区别是:在相同的噪声强度下,当Ek=-88.5时的周期一放电比当Ek=-88时的放电偏少,主要原因有两个:一是分岔参数距离分岔点的远近问题,另一个是分岔参数所处的稳定极限环和平衡点的吸引域的大小问题.整数倍节律的峰峰间期序列虽都具有明显的分层现象,但当Ek=-88.5(Hopf分岔点左)时的峰峰间期序列相对散,而当Ek=-88(Hopf分岔点右)时的峰峰间期序列主要集中在周期一放电.但两者整数倍节律模式的峰峰间期序列的回归映射都成晶格状,如图2(d)和(d1)所示.这些不仅体现整数倍的特征,还体现了在Hopf分岔点左、右得到的整数倍节律的区别,这不仅有利于我们模拟数据的选取,还有利于我们更好的了解整数倍节律产生的机制.
4 随机INa,p+IK模型中的随机自共振
由于随机INa,p+IK模型系统含有噪声项,所以由于噪声的影响,在Hopf分岔附近有随机共振现象产生.现取Ek=-88.5(Hopf分岔点左)为例说明,当噪声强度为零时,初值取为(V,n)=(-60.46571,0.05226),系统处于阈下振荡或者静息态,如图3(a)所示;当噪声强度比较小时,神经元大部分时间在固定点(静息电位)附近波动,只偶尔才激发,这是由噪声超过阈值而造成的,如图3(b)所示;当噪声强度略为增大时,噪声会激发神经元的发放,放电增多,如图3(c)所示,而且,在几个主要的频率附近出现峰电位,这个频率是频谱图最高峰处所对应的频率,如图3(d)所示.由图3(b)和(c)可以看出,在噪声强度较弱的情况下,膜电位的时间序列中的低阈值振荡和稀疏的周期振荡序列的间隔非常明显.

图3 当Ek=-88.5时,随机INa,p+IK模型在不同噪声强度下膜电位的时间历程图:(a)D=0;(b)D=0.05;(c)D=0.5;(d)随机INa,p+IK模型在不同噪声强度下功率谱
描述共振特征的一种常用手段是信噪比[8],这里采用胡岗[9]在1993年提出的一个定义:

上式中H代表经过快速傅立叶变化后所得的频率谱上峰的高度,ωp是峰高处对应的频率(也被叫做基频),Δω表示峰的半峰高度时的频率宽度.
在处理内随机共振情况时,信噪比还有另一种比较常用的定义,其定义如下

用公式(3)计算其信噪比,如图4(a)所示,当Ek的值增大时,信噪比没有大的变化,但对于每一条曲线(即Ek固定)上都存在一个最佳噪声强度使得信噪比的值最大,且信噪比取最大值所对应的噪声强度都约为D=10.这种共振性质也可以用另一种方式来描述,即用公式(4)计算其信噪比,如图4(b)所示,当Ek的值增大时,信噪比没有大的变化,但在每一条曲线(即Ek固定)上都存在一个最佳噪声强度使得信噪比的值最大,且信噪比取最大值所对应的噪声强度都约为D=10.上述两种信噪比的计算方式都体现了随机自共振(或相干共振)的特性.

图4 当Ek不同时,随机INa,p+IK模型中通过功率谱计算β1、β2与噪声D的关系图:(a)是β1和logD的关系图;(b)是β2和logD的关系图
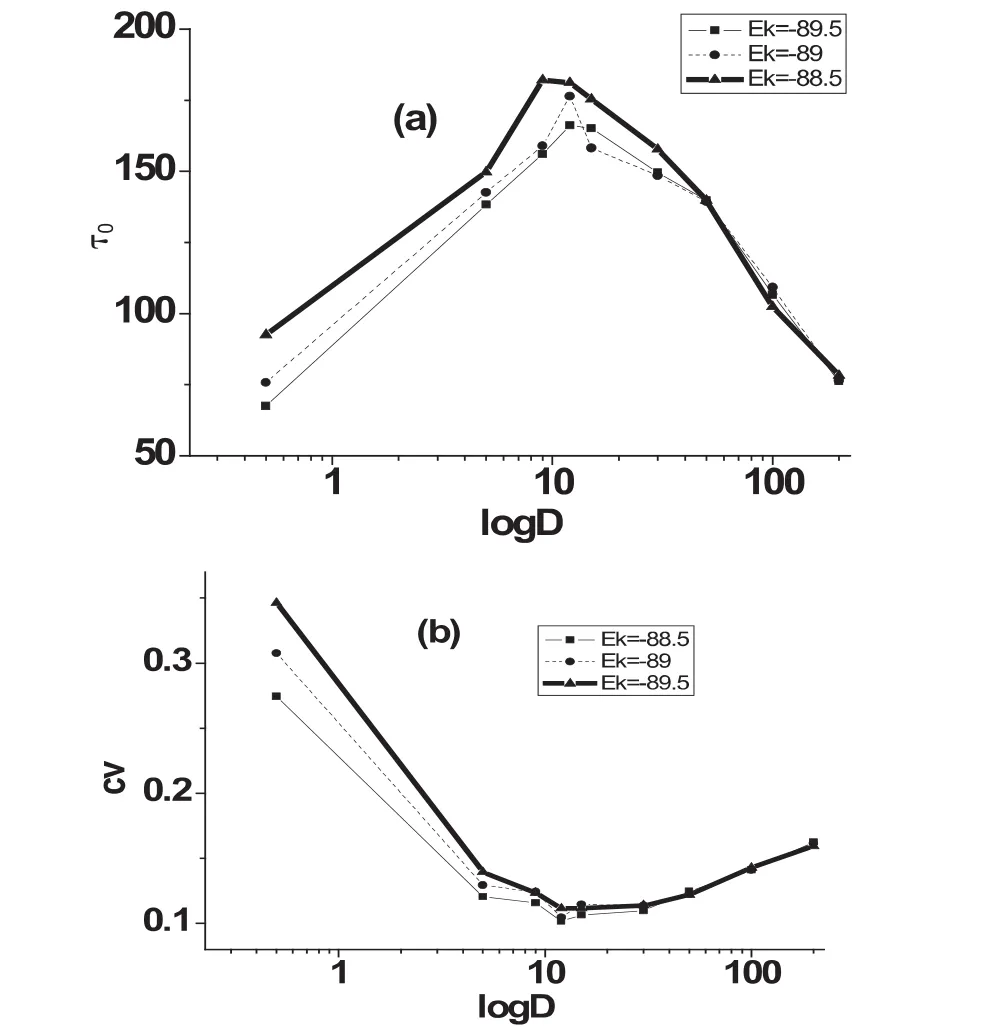
图5 当Ek不同时,随机INa,p+IK模型,(a)相关时间τ0与logD的关系图;(b)变异系数CV与logD的关系图
5 结论与讨论
本文通过研究II型兴奋对应的INa,p+IK模型中的超临界Hopf分岔附近的自发放电节律的特征:ISI序列,回归映射,ISI统计直方图(含有指数衰减特征),ISI随机序列的变异系数等,探讨了在无外界的刺激下产生的随机性整数倍节律模式.并且,整数倍节律模式存在于INa,p+IK模型的超临界Hopf分岔附近的周期一与静息之间.这与整数倍节律模式存在于Chay模型的亚临界Hopf附近的周期一与静息之间,而未出现于超临界Hopf分岔附近的周一与静息之间的结论[11]有些不一致.这是由于亚临界Hopf分岔的共存区间特别小,它表现的性质与超临界Hopf分岔的性质很接近的原因.还有并不是所有的超临界Hopf附近都可以产生整数倍节律模式,由于整数倍节律模式必须有一个基本的放电频率,所以我们选择超临界Hopf时选择极限环变化比较稳定的较易出现整数倍节律模式.在本文中,随机性整数倍节律模式都是高斯白噪激励的随机自共振现象.但其它噪声也可以激励出随机自共振现象,如伪单色噪声激励的FHN模型可以在Hopf分岔点附近区域产生阵发周期一随机共振现象[12].
〔1〕Rose J.E.,Brugge J.F.,Ardertson D.D.and Hind J.E.. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel mongkey[J]. Neurophysiol,1967,30:769.
〔2〕Douglass J.k.,W ilkens L.,PantazelouE.,Moss F.Noise enhancement of information Transfer in crayfish mechanoreceptors by stochastic resonance[J].Nature, 1993,365:337-340.
〔3〕Gu H.G.,RenW.,Lu Q.S.,W u S.G.,YangM.H.,ChenW.J. Integermultiplespiking inneuralpacemakersw ithoutexternal periodicstimulation[J].PhysLettA,2001,285:63~68.
〔4〕古华光,任维,杨明浩,陆启韶.神经起步点产生一种新型簇放电节律-阵法周期1节律[J].生物物理学报,2002,18 (4):440-446.
〔5〕古华光,李莉,杨明浩,刘志强,任维.实验性神经起步点产生的整数倍簇放电节律[J].生物物理学报,2003,19(1): 68-72.
〔6〕Izhikevich E.M.Dynam ical Systems in Neuroscience:The Geometry of Excitability and Bursting[M].The M IT Press, 2005.
〔7〕Mannella R.,Palleschi V.Fast and precise algorithm for computer simulation of stochastic differential equations[J]. Phys Rev A,1989,40:3381-3386.
〔8〕Benzi R.,Sutera S.,Vulpiani A.The mechanism of stochastic resonance[J].PhysA,1981,14:453~457.
〔9〕Hu G.,Ditzinger T.,N ing C.Z.Stochastic resonancew ithout externalperiodic force[J].PhysRev Lett,1993,71:807~810.
〔10〕Pikovsky A.S.,Kurth J.Coherence Resonance in a Noise-Driven Excitable System[J].Phys Rev Lett,1997, 78:775~778.
〔11〕杨卓琴.神经元模型放电节律模式的非线性动力学研究[D].北京:北京航空航天大学,2003.
〔12〕古华光.实验性神经起步点的自发放电节律和心脏电活动的非线性动力学分析[D].北京:北京航空航天大学,2000.
Q42
A
1673-260X(2014)07-0003-04
内蒙古自治区自然科学基金面上项目资助(2012MS0103)
