稀疏卷积非负矩阵分解的语音增强算法
2014-07-25张立伟张雄伟
张立伟 贾 冲 张雄伟 闵 刚,2 曾 理
(1.解放军理工大学指挥信息系统学院,南京,210016;2.西安通信学院基础部,西安,710106)
引 言
语音增强是语音信号处理中的重要领域,其主要目的是从带噪语音信号中尽可能提取纯净的原始语音或原始语音参数,在语音编码、语音识别和听觉辅助等领域具有重要的应用价值。20世纪70年代以后,随着数字信号处理理论的发展成熟,人们开始采用信号处理的方法研究和实现语音增强问题。最具代表性的算法是Boll提出的谱减法(Spectral subtraction,SS)[1],其思想简单直观、易于实现,但该方法假设在有声段噪声是固定的,且依赖话音激活检测技术(Voice activity detection,VAD),在非平稳噪声环境和低信噪比条件下,效果并不理想。多带谱减法(Multi-band spectral subtraction,MSS)是将噪声频谱划分为互不重叠的频带,分别在不同频带采用不同的谱减参数进行增强处理[2]。该算法效果要明显好于传统谱减法,但仍需要VAD过程。基于非负矩阵分解(Nonnegative matrix factorization,NMF)[3]的语音增强算法是通过训练构造语音和噪声的字典并将其组合成一个联合字典,利用非负矩阵分解更新带噪语音在联合字典下的投影系数,实现语音和噪声的分离。然而,非负矩阵分解算法只是在频域进行字典学习,学习得到的字典中的原子通常只是一维信号,缺乏有效表征原始信号的结构特征,也没有考虑帧与帧之间的相关性。针对上述不足,Smaragdis提出一种新的矩阵分解算法——卷积非负矩阵分解(Convolutive nonnegative matrix factorization,CNMF)[4]。 利 用 CNMF 算 法 分 解 语 音 信号,得到的时频字典能够更好地保留语音信号中的个人特征信息及帧间相关性。孙健等率先将该算法运用到语音转换中,提出一种基于卷积非负矩阵分解的语音转换方法[5],获得了较好的转换效果。随后,黄建军等人将该算法运用到语音增强中,提出了一种时频学习单通道语音增强算法[6]。虽然该算法取得了较好的增强效果,但是对语音信号中的一些时频特征描述仍不够完善。本文在卷积非负矩阵分解的基础上,考虑到语音信号在时频域的稀疏性,提出了基于稀疏卷积非负矩阵分解(Sparse convolutive nonnegative matrix factorization,SCNMF)的语音增强算法。
1 稀疏卷积非负矩阵分解
1.1 卷积非负矩阵分解
卷积非负矩阵分解是非负矩阵分解的二维扩展,可以用如下数学模型来表示
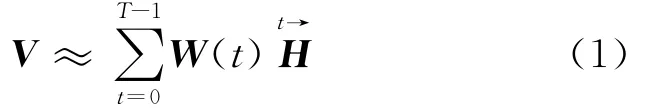
式中:V∈R≥0,L×N为待分解的矩阵;W(t)∈R≥0,L×R和H∈R≥0,R×N分别为时频原子和相应的时变增益系数;()运算符表示向右移动矩阵i列并将最左边的i列补零。CNMF的数学模型可以理解为用非负矩阵集W和非负矩阵H的卷积来表示待分解非负矩阵V,故称为卷积非负矩阵分解。CNMF的目标就是寻找一系列的非负矩阵W(t)和H,使其卷积的结果尽可能地逼近矩阵V。使用KL散度作为目标函数即

式中:V为V的估计
KL散度是在泊松噪声假设条件下求解非负矩阵W(t)和H的最大对数似然解[3],用于描述与V的逼近程度。通过对目标函数的优化可以得到乘性迭代规则[4]
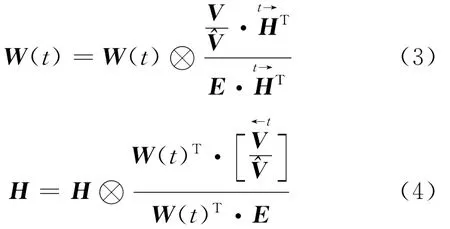
式中:⊗为矩阵元素相乘运算符;E为元素都为1的矩阵。
1.2 稀疏卷积非负矩阵分解
由于语音信号在时频域存在稀疏性,因此采用稀疏非负矩阵分解算法能够更好地反映语音的这种特征,且该算法收敛速度快,存储空间小[7]。Paul等在CNMF算法中加入稀疏性约束,即对编码矩阵H进行稀疏性约束[8],得到的时频字典W(t)能够更为详细地包含语音的特征信息。通过控制H的稀疏度可以使W(t)成为过完备时频字典。对H进行稀疏性约束,式(2)可以改写为
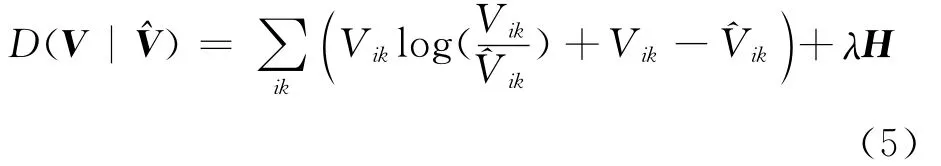
式中λ为稀疏因子,用于控制编码矩阵的稀疏性和重构时语音的失真度。
增加稀疏性约束后带来一个新问题:增加的稀疏约束项λH是单调递增函数,当W(t)增大,H减小时,(W(t)→αW(t),H(t)→(1/α)H(t),其中α≥1),目标函数值将会减小。在这种情况下,等式右边的第一项并不会受到影响,而第二项则会减小,必然导致W(t)的元素值趋于无穷大,H的元素值趋于零。因此,为了控制W(t)和H中元素值大小,需要引入另一个约束条件,即令‖W(t)‖2实现归一化。
与CNMF算法的乘性迭代规则相似,利用梯度下降法对目标函数(5)优化可以得到如下的乘性迭代规则[7]

SCNMF算法中对W(t)和H的求解采用迭代求解方式,具体过程如下:
(1)开始;
(2)初始化W(t)和H;
(3)重复;
(4)k←k+1;
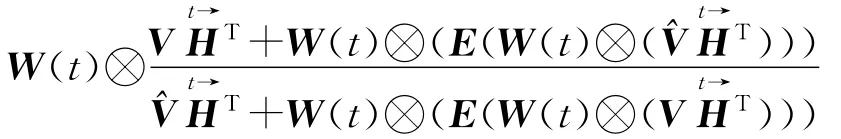
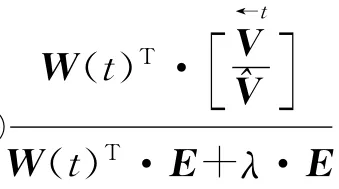
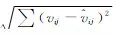
(8)结束:最终得到W(t)和H。
1.3 CNMF和SCNMF处理语音信号的结果对比
取TIMIT标准语音库中“SA1”纯净语音,通过短时傅里叶变换(Short-time Fourier transform,STFT)得到幅度谱V。当语音字典原子数目R=40,时间跨度T=8,稀疏因子λ=0.05时,通过CNMF和SCNMF算法分别对V进行分解,结果如图1所示。
通过图1,可以看出SCNMF算法相对于CNMF算法,更多地保留了信号的特征信息,特别是中高频段的信息,并将这些信息反映在时频字典上,如图1(c,e)所示。正是由于采用SCNMF算法对语音信号分解时生成了过完备时频字典,使得其时变增益相较于CNMF算法而言更加稀疏,如图1(d,f)所示。根据信号稀疏表示原理,信号表示得越稀疏,分离去噪效果越好,同时也会造成更多的语音失真[9]。尽管CNMF算法分离的时变增益也具有稀疏性,但是相对而言,SCNMF算法中加入了稀疏因子λ,通过调整λ的取值,能够在去除残余噪声和减小语音失真方面得到折中,从而能得到更加准确的增强语音。
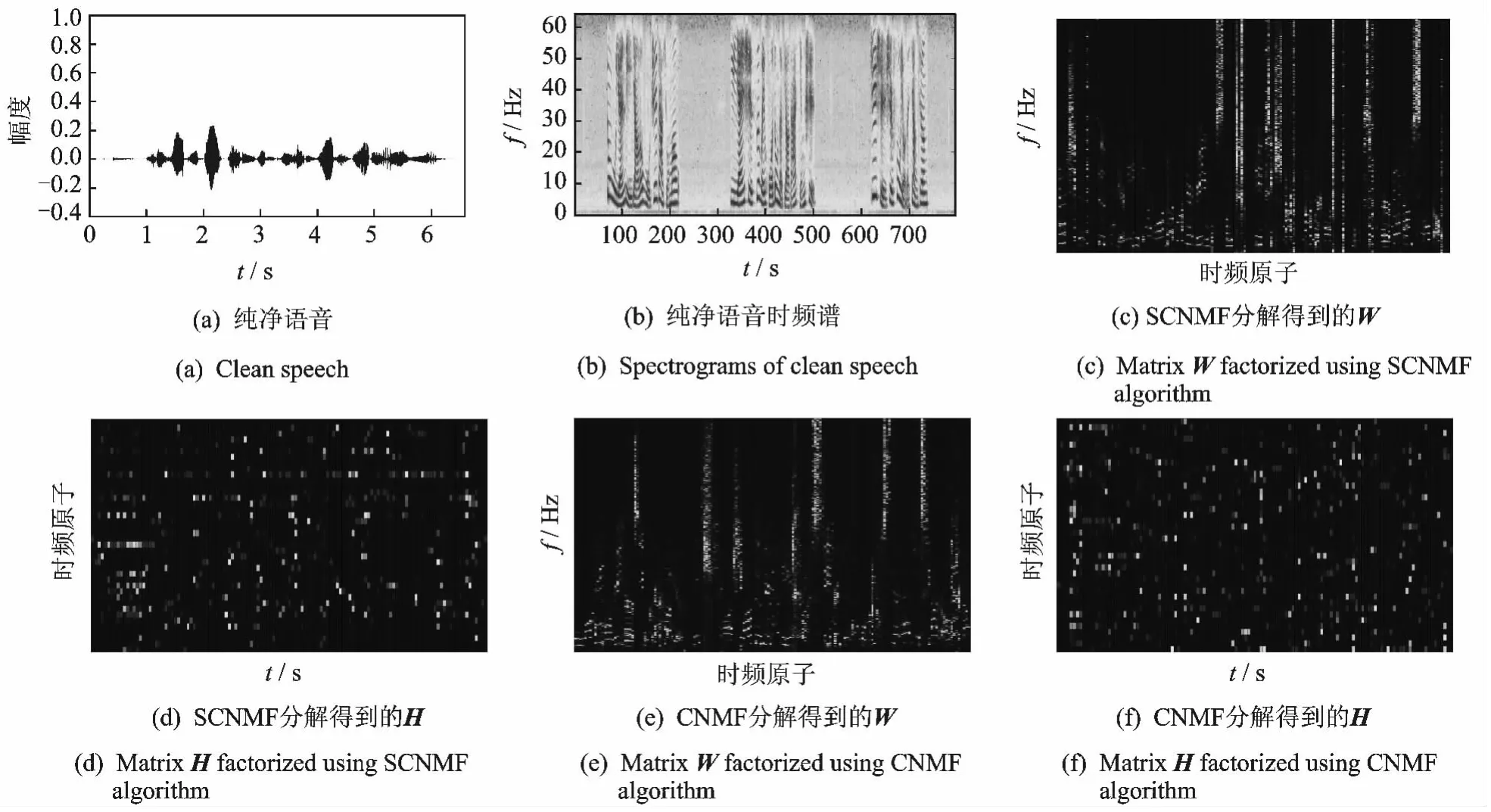
图1 “SA1”纯净语音及其时频谱以及分别用CNMF和SCNMF算法分解得到的时频字典和时变增益Fig.1 Waveforms and spectrograms of speech″SA1″,and basis matrices and coefficient matrices factorized from″SA1″using CNMF and SCNMF algorithms respectively
2 基于稀疏卷积非负矩阵分解的语音增强
与传统的基于字典学习的语音增强算法相似,本文提出的基于稀疏卷积非负矩阵分解的语音增强算法分为字典学习和增强两部分。假设语音信号和噪声信号均为加性信号,则带噪语音信号y(t)可以表示为

式中:s(t)为纯净语音信号;n(t)为噪声信号,二者相互独立。算法可划分为学习和增强两个阶段,总体框架如图2所示。
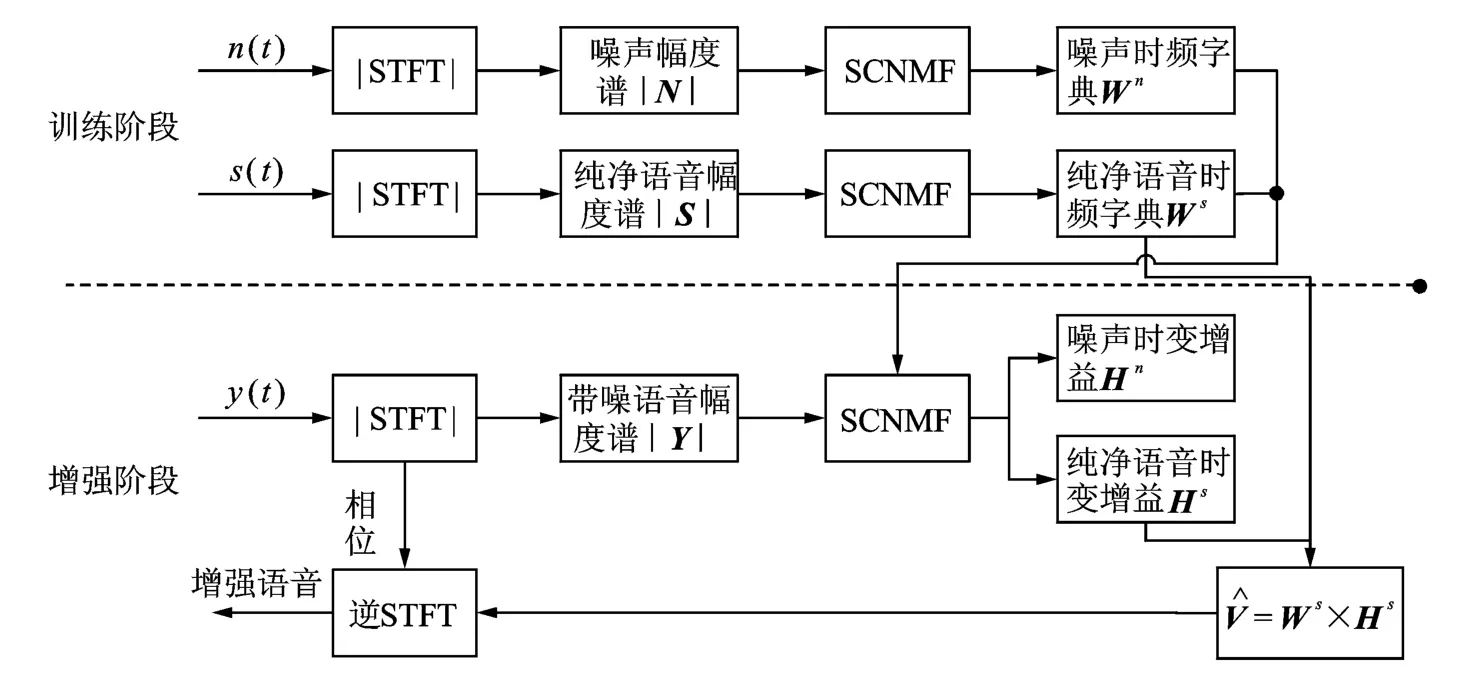
图2 SCNMF语音增强算法总体框架Fig.2 Framework of speech enhancement based on SCNMF algorithm
字典学习阶段:首先通过STFT得到纯净语音和噪声的幅度谱,然后利用稀疏卷积非负矩阵分解算法分别将纯净语音和噪声幅度谱分解为过完备时频字典Ws,Wn和时变增益Hs,Hn,将过完备时频字典Ws和Wn保存下来作为增强阶段的先验信息。
增强阶段:通过STFT得到带噪语音幅度谱,将幅度谱作为稀疏卷积非负矩阵分解的输入,用训练阶段保存的纯净语音和噪声过完备时频字典Ws和Wn作为先验信息,通过分解得到语音的时变增益Hs和噪声时变增益Hn。在重构出语音和噪声的幅度谱之后,运用逆STFT分析得到增强后的语音信号。
3 仿真结果
本节将通过实验仿真,首先讨论稀疏因子对SCNMF算法的影响,从中找出稀疏因子λ的最优值。然后,再将本文提出的语音增强算法与多带谱减法、基于NMF和CNMF的语音增强算法进行比较,评估本文算法的性能。
3.1 稀疏因子对算法的影响分析
从1.1节中可知,影响CNMF算法增强效果主要有2个参数,即语音字典原子数目R和时间跨度T。在实验中发现,40个时频原子就足够描述语音的声学特征,更多的原子数目会增强算法计算量,性能提升却很有限,因此语音字典原子数目R设置为40个。与文献[6]中的参数设置一致,在这里时间跨度T=8。而对于SCNMF算法,影响其增强效果主要有3个参数,即语音字典原子数目R、时间跨度T和稀疏因子λ。R和T的选取,根据CNMF算法中的取值不变,本节主要讨论稀疏因子λ的选取。根据文献[7]可知,稀疏因子λ为大于零的实数,它主要用于调节算法总体误差和稀疏度的关系。其取值越大,时变增益矩阵H越稀疏,反之亦然。由1.3节可知,时变增益矩阵H的稀疏度与增强后得到的语音质量具有紧密联系。λ值越大,H越稀疏,则增强后的语音将包含更少的残余噪声。但是,H越稀疏在增强过程中将会有更多的语音成分丢失,从而造成更大的语音失真。为了实现对语音失真和残留噪声之间的权衡,得到更好的增强效果,本节设计了以下实验,在总体性能最优的条件下对稀疏因子λ进行优化选择。
实验中,将纯净语音中分别加入F16,M109,Babble三种典型噪声,分别得到信噪比为-5,0,5,10dB的带噪语音。获取带噪语音的时频谱时采用Hamming窗函数,窗长512,帧移256。在3.2节的算法性能比较时采用同样的参数设置。稀疏因子λ的取值范围设定为[0,1]。在实验中发现,算法性能在λ较小时比较敏感,因此λ步长采用不等间隔,在[0,0.1]时采取较小步长(0.01),在[0.1,1]时采取较大步长(0.1)。对数频谱距离(Log-spectral distance,LSD)反映了语音频谱失真的度量,LSD值越小,说明算法的增强效果越好。因此本文采用LSD测度作为参数优化过程中的评价指标。
图3-5曲线为所有实验后得到的LSD值。显然,对于不同信噪比,在[0,0.05]区间,LSD 值先上升而后降至最低点,在[0.05,1]区间,LSD值上升至一定程度逐渐趋于平稳(当然存在个别奇异点,这里不再考虑)。这一结果表明在不同信噪比下λ=0.05是一个较理想的最优值。
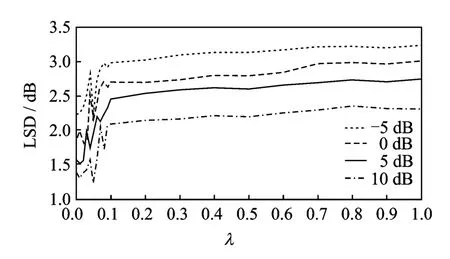
图3 混入F16噪声时稀疏因子λ对算法性能影响Fig.3 Performance of the algorithm affected by sparse factorλmixed with F16noise
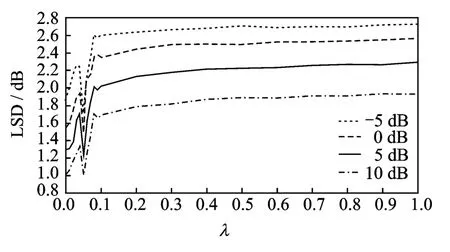
图4 混入M109噪声时稀疏因子λ对算法性能影响Fig.4 Performance of the algorithm affected by sparse factorλmixed with M109noise

图5 混入Babble噪声时稀疏因子λ对算法性能影响Fig.5 Performance of the algorithm affected by sparse factorλmixed with Babble noise
3.2 与其他算法的性能比较
为了验证本文算法的有效性,将其与多带谱减法、基于NMF和CNMF的语音增强算法进行比较。实验中,取纯净语音为8kHz采样、16b量化的标准女声信号。噪声取自Noisex-92噪声库中的F16飞机噪声、M109坦克噪声和Babble噪声。通过MATLAB将纯净语音信号与噪声信号进行混合,分别生成信噪比为-5,0,5,10dB的带噪语音。
本文采用3.1节所述的对数频谱距离LSD和客观质量评估方法(Perceptual evaluation of speech quality,PESQ)对语音增强算法的性能进行比较。PESQ取自2001年国际电信联盟(ITUT)推出的P.862标准,用来评价语音的主观试听效果,能够很好地反映语音信号的感知质量,PESQ得分越高表示增强效果越好。
表1-2分别给出了4种算法在不同信噪比条件下增强语音的LSD值和PESQ值的比较情况,由表可以看出,相对于多带谱减法、基于NMF和CNMF的语音增强算法,本文提出的基于SCNMF的语音增强算法具有更好的增强效果。
同时可以看出,当在低信噪比情况下,本文提出的基于SCNMF的语音增强算法较其他3种算法优势更加明显,而在高信噪比情况下,本文的算法提升性能效果不明显。这是由于在低信噪比情况下,相对于其他3种算法,基于SCNMF的语音增强算法分解得到的过完备时频字典能够在充分去除残余噪声的条件下,更多地保留语音成分。
最后,对本文所提出算法的复杂度进行简单分析。本文算法的计算量包括STFT、语音过完备时频字典与时变增益更新和逆短时傅里叶变换(ISTFT)。,由SCNMF算法的迭代流程可知,整个算法的计算量主要集中在过完备时频字典和时变增益的迭代求解,即式(6-7)的矩阵运算上。设带噪语音幅度谱频率点数为L和整个语音帧数目为N,为矩阵分解的秩为R,时频原子大小为T,根据文献[4]分析,CNMF的时间复杂度为O(TLNR),而本文算法的时间复杂度与CNMF算法处于同一级别,因此其时间复杂度也是O(TLNR)。
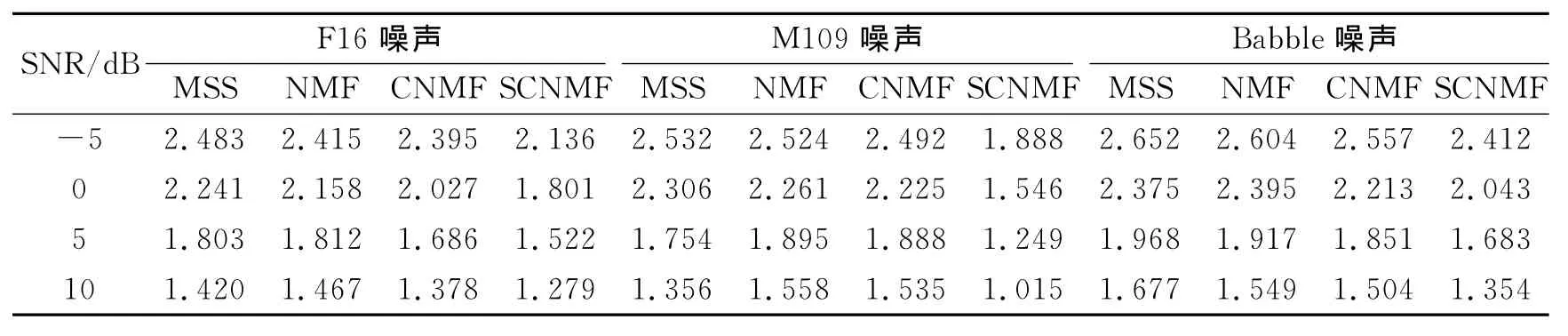
表1 增强语音的对数谱失真Table 1 LSD of enhanced speech
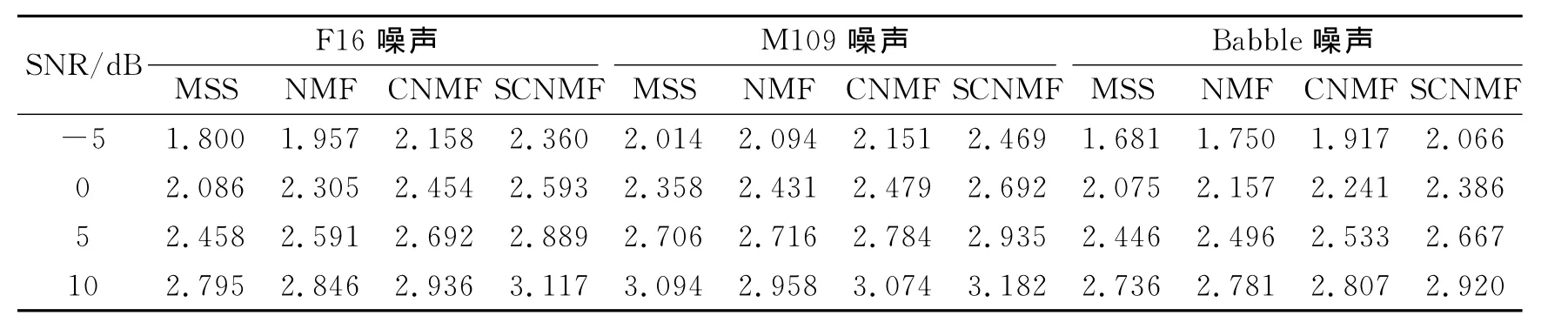
表2 增强语音的PESQ得分Table 2 PESQ of enhanced speech
4 结束语
本文提出了一种基于SCNMF的语音增强算法,该算法通过训练得到的先验知识对带噪语音进行增强。实验表明,在非平稳噪声和低信噪比条件下,相对于传统的增强算法,在不提升算法复杂度的同时能够更好地抑制背景噪声,取得了良好的增强效果。虽然本文提出的方法较传统的增强算法有一定的改进,但基于SCNMF的语音增强方法仍存在一些不足:部分参数值的选取依赖于实验结果或经验值,特别是本文对于稀疏因子的选取,缺乏理论验证;本文方法在字典学习阶段仍然需要语音信息,这在一定程度上制约了算法的适用范围。在今后的工作中,将以上述问题为方向,对语音增强算法进一步进行研究和改进。
[1]Boll S.Suppression of acoustic noise in speech using spectral subtraction[J].IEEE Transactions on A-coustics Speech,and Signal Processing,1979,27(2):113-120.
[2]Kamath S,Loizou P.A multi-band spectral subtraction method for enhancing speech corrupted by colored noise[J].IEEE Trans Acoust,Speech Signal Process,2002,8(4):164-168.
[3]Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401(10):788-791.
[4]Smaragdis P.Convolutive speech bases and their application to supervised speech separation[J].IEEE Trans on Audio,Speech and Language Processing,2007,15(1):1-12.
[5]孙健,张雄伟,曹铁勇,等.基于卷积非负矩阵分解的语音转换方法[J].数据采集与处理,2013,28(2):141-148.
Sun Jian,Zhang Xiongwei,Cao Tieyong,et al.Voice conversion based on convolutive nonnegative matrix factorization[J].Journal of Data Acquisition and Processing,2013,28(2):141-148.
[6]黄建军,张雄伟,张亚非,等.时频学习单通道语音增强算法[J].声学学报,2012,35(5):539-547.
Huang Jianjun,Zhang Xiongwei,Zhang Yafei,et al.Single channel speech enhancement via time-frequency dictionary learning[J].Acta Acustica,2012,35(5):539-547.
[7]Ohoyer P.Non-negative matrix factorization with sparseness constraints[J].Journal of Machine Learning Research,2004(5):1457-1469.
[8]O′Grady P D,Pearlmutter B A.Convolutive non-negative matrix factorization with sparseness constraint[C]∥International Workshop on Machine Learning for Signal Processing.Maynooth,Ireland:IEEE,2006:427-432.
[9]Zibulevsky M,Pearlmutter B A.Blind source separation by sparse decomposition in a signal dictionary[J].Neu Comp,2001,13(4):863-882.
