基于遗传算法的灌溉管网优化设计

刘雪侠 余鲁江

（1.扶风县防汛抗旱指挥部办公室 陕西 扶风 722000；2.扶风县水利电力工作队 陕西 扶风 722000）

我国60%以上的用水量用在农业上面，而其中90%以上都在灌溉方面。我国目前灌溉用水的利用率较低，探索和发展节水灌溉成为灌溉发展的必然趋势。渠道输水和管道输水分别是灌溉中两种主要的输水方式。其中管道输水具有减小蒸发量和渗漏损失、提高土地利用率、适应地形能力强、缩短灌水周期和方便田间管理等优点[1]。因此，管道输水是节水灌溉的一个重要发展方向。输水管道的设计较为复杂，耗费较大的人力、财力和物力。其中管网部分的投资就占到工程总投资的60%以上。对管网进行满足特定约束条件下的优化设计，可以大大节省工程投资。管网的优化设计包括管网布置的优化设计和管径的优化设计两个方面[2]。管网布置的优化设计较为复杂，它所涉及的因素较多，比如地形和人员的经验等，目前这方面的优化研究工作相对较少，但也有一部分人在进行相应的研究[3]。管径的优化设计是在管网布置确定的情况下，对管径进行优化设计计算，管径优化设计是一个多目标非线性优化问题，目前，研究者主要就是研究这方面的问题[4]。本文结合某工程实例，运用遗传算法分别对管网的布置和管径进行优化设计。分别建立管网布置优化设计模型和管径优化设计模型，然后采用matlab工具箱中的遗传算法进行求解。

1 遗传算法基本原理和优化模型

遗传算法是模仿自然界生物遗传和变异而发展起来的，是一种高度的数学抽象。遗传算法的本质其实还是一种迭代算法。遗传算法首先对由多个个体所组成的初始种群进行搜索，通过遗传、重组和变异操作形成一个新的种群。遗传算法的进化过程实际上就是以应用概率的方式逐渐逼近最优解的过程。遗传算法具体进化过程为，首先对优化问题的解产生编码，就是我们所说的染色体，运用染色体组合成一组群，即前述所说的种群，然后运用适应度函数对各染色体进行分析，评价和度量各染色体的好坏，为接下来的遗传操作提供依据，适应度越大，遗传操作中染色被选择的机率就会越大。为了使优化的结果更加全局和准确，避免局部收敛的影响，在遗传操作中加入了交叉和变异的特定操作。经过上述计算过程，就可以获得一个已经优化了的新的种群。然后再对该种群重复进行上述遗传操作，最终将得到问题的最优解。遗传算法可以简要总结为编码、适应度函数分析、遗传操作、终止这几个步骤。本文就是运用上述遗传算法对管网布置进行优化设计，本文的计算借助matlab的遗传算法工具箱来实现。

管网布置优化的基本目的是，首先要满足节水灌溉的基本要求，在此基础上期望使工程量最小，同时达到管线最短。而管径的优化设计是在管网布置确定后，综合考虑费用和能耗这一对矛盾的目标，选择相应最优的管径组合。管径较大时，相应的投资费用大，但水头损失较小。而管径较小时，投资费用小，但是水头损失较大，能耗也较大。管网布置的优化和管径的优化存在一定的联系，对于小型的灌区，将两者统一进行优化可以得到较为理想的结果。

本文采用线性规划模型进行管网优化，该模型较易采用已有的算法进行求解。一般的线性规划模型的标准形式如下式所示：

式中，Xi——决策变量，是最优化所得的解；

Ci——费用系数，它是一个常数；

Aij——约束系数，Bi则为右端常数项。

目前，管网布置多采用树状管网，它的输水主要靠地表的落差来提供动力。针对树状管网，为了实现最优和最低的投资目标，此时管径的长度Xij是主要的优化变量，针对树状管网的优化规划模型如下：

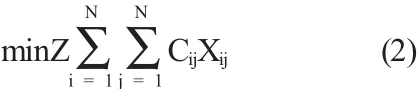
工作压力的约束：

式中，Z——管网的总造价；

N——管段的数量；

M——标准管径的数目；

Cij——管段的造价系数；

Lj——管段的长度；

E0——自由水面高度；

M（t）——管段数；

Qij、Dij、Xij——分别是流量管径和管长；

α、f、m、n——分别为水头损失相关参数；

Ek——地面标高；

Hkmin——所必须满足的最小水头。

本文将针对上述线性规划模型，运用遗传算法进行树状管网的优化设计分析。

2 实例计算

2.1 工程概况

有一小型灌区，位于平原地区，农田用水量较大，最大要求用水量大约达275m3/s，由于天然水源不足，需要引水进行灌溉。原先设计采用引水渠进行引水供水，但由于水源较远，同时渠道占用面积较大，准备改用管道输水灌溉，通过挖取深井作为水源，安装水泵将水抽出。本工程采用树状的管网布置，以提高引水利用率，节约成本和土地。初步设计该小型灌区共有8个供水节点，通过井点水源将水输送到供水节点进行灌溉。工程地形条件相对较为复杂，存在一定的高差，整个灌溉区域的平面面积大约为500m×600m。8个供水节点合理分布在灌水区域的各个位置，以形成全面经济的输水和灌溉管网。工程输水管初定采用PVC管，作为主要输水管道，并对管径组合进行优化。设计者根据经验，初步拟定了各供水节点之间的连接图，如图1所示，其中设计可能供水的管段有20条。由于用水的要求，管网各供水节点的最低压力水头为10m，管道中的最小流速必须大于0.5m/s，但是最大值不能超过3m/s。管网的设计中，各管段和节点的基本数据分别如表1和2所示。鉴于该工程的实际特点，本文运用遗传算法对该工程管网布置和管径的组合进行优化计算，并将计算结果与传统优化设计方法的计算结果进行比较分析。

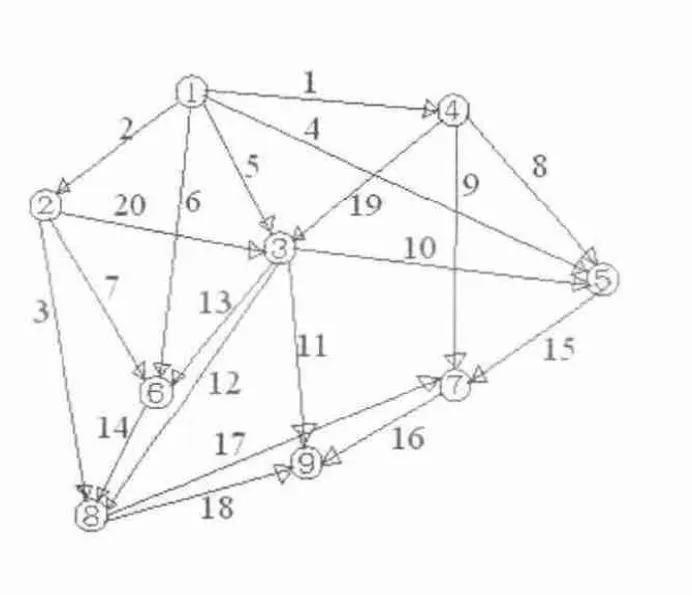
图1 管网初步连接图

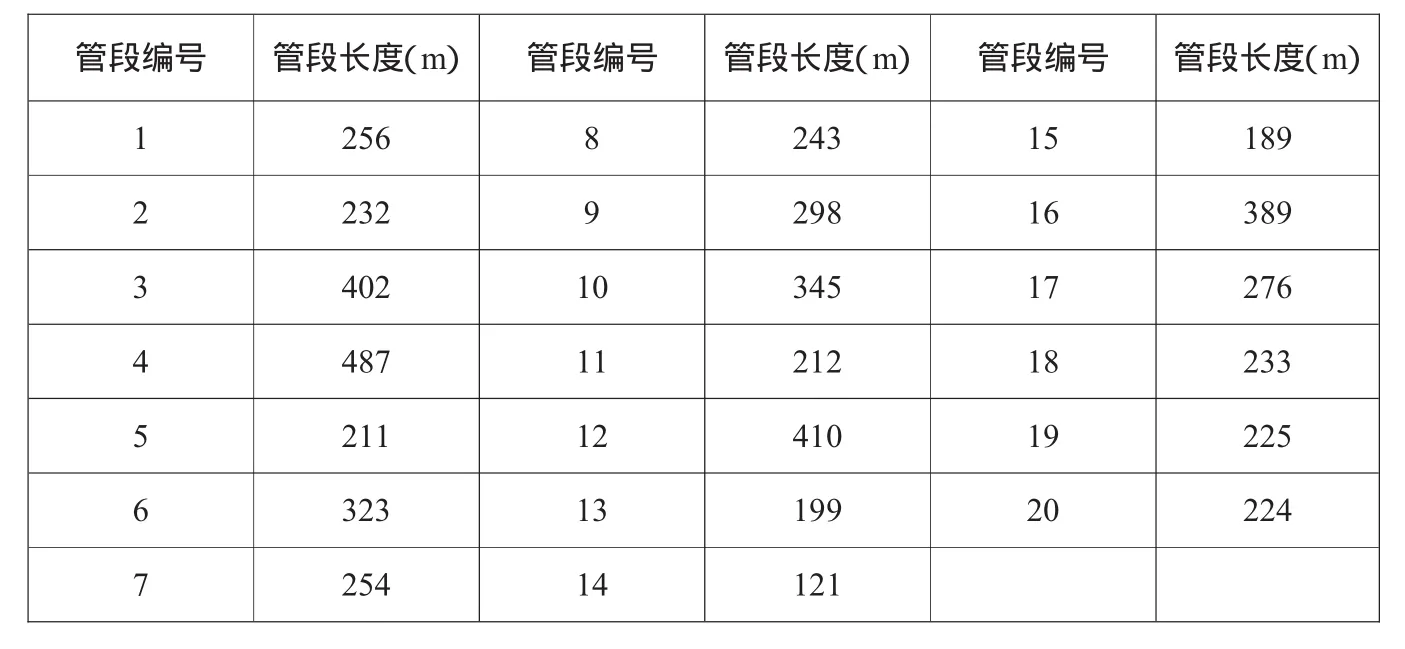
表1 管段长度数据

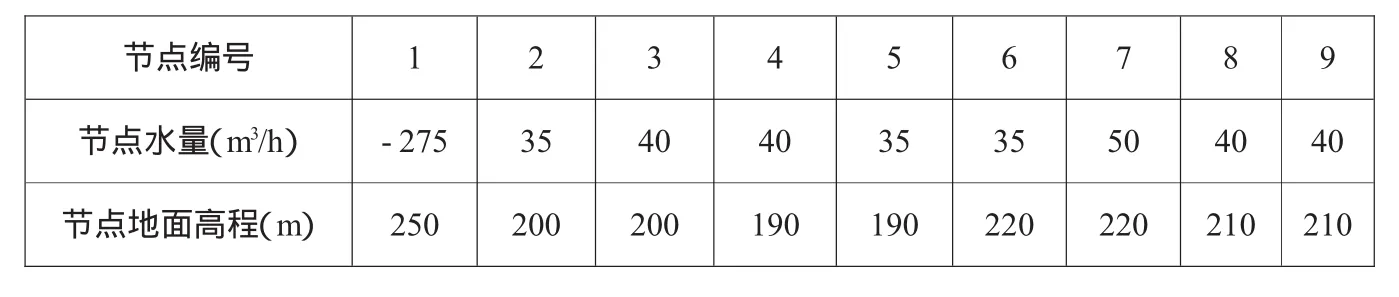
表2 节点数据

表3 管径优化结果

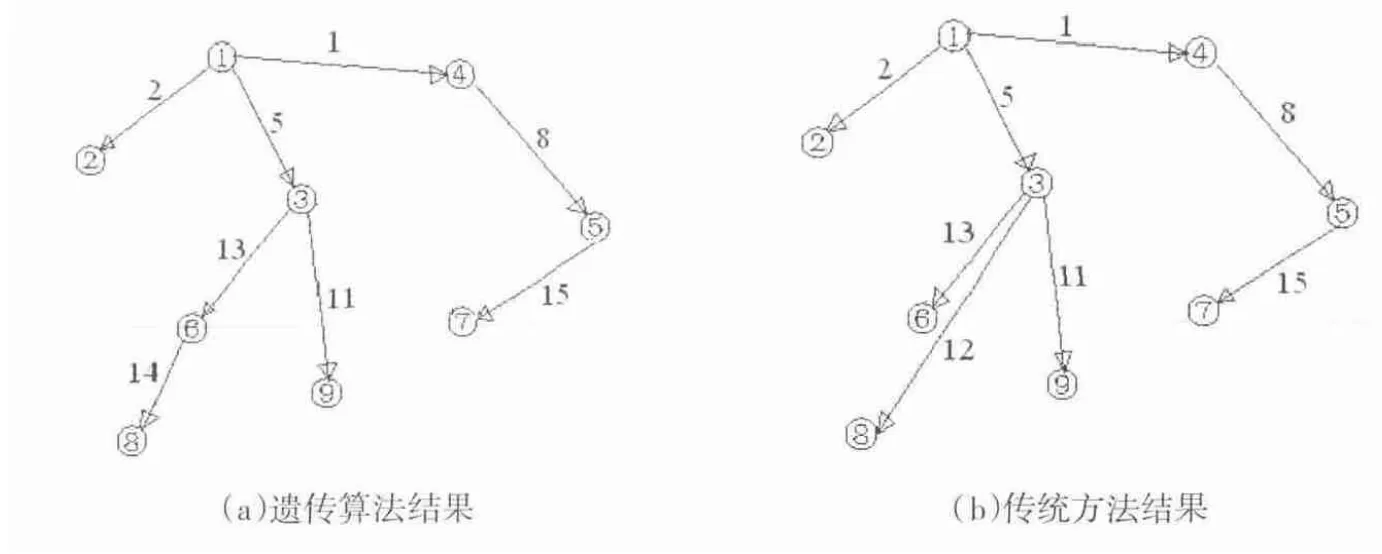
图2 管网优化布置图

2.3 灌溉管网优化设计结果分析

本文运用matlab中的遗传算法工具箱进行管网的布置和管径组合的优化设计计算。在matlab中进行适当的编程设置，本文计算时，设置种群的初始规模为NIND=60，种群的计算代沟为GGAP=0.9，进行多次进化迭代计算，设置遗传操作的终止代数为MAXGEN=110，通过运用概率的方式逼近最优解，最终计算得出符合实际情况，并且造价最小的优化方案。计算所得管径组合和管网布置的优化结果分别如表3和图2所示。

对于图2中遗传算法所得结果，运用本文的遗传算法，进行了多次计算，所得结果均保持不变，说明该结果即为遗传算法所得的最优布置结果。该结果下管网布置较为简洁，所得管线的总长度为2530m，管线的总投资为15243元。传统的优化设计结果下，管网的布置结果如图2（b）所示，所得管线总长度为2879m，管线的总投资达到20100元。相对于传统方法，遗传算法所得管网布置结果，管线总长度减小349m，节省投资4857元，占总投资的24.3%。说明遗传算法相对于传统的优化设计方法，实用性更强，所得结果更加合理。遗传算法所得结果下，节点3的工作负担较传统方法相对较小。传统方法中，节点3不仅需要供水，还承担向其它3个节点供水的任务，传统方法所得结果问题较为突出，容易产生不协调问题；由于遗传算法考虑了人为的各种因素，可以很好地避免这类问题的产生。

由表3中管径组合的优化结果可知，优化所得结果，满足管网水头和管道流速的基本条件，计算所得管径的分布较为合理，基本呈现离水源近时管径和流速相对较大的客观规律。所得管径连接较为合理，没有出现突变过大的情况。所得各管段的计算流量可以很好地满足各供水节点的供水要求。

3 结论

本文采用遗传算法用于灌溉管网的优化设计，运用matlab中的遗传算法工具包实现管网的优化设计计算。结合工程实例，建立管网布置和管径组合优化模型，运用遗传算法进行求解，并与传统优化设计方法计算结果进行对比分析。实例计算表明，遗传算法可以同时进行管网布置和管径组合的优化计算，所得结果相对于传统优化设计方法，管网单位布置更加合理，工程的投资也有效减小。本文所得实例结果合理，可以作为同类工程的参考，同时，采用遗传算法进行管网优化设计，也可为同类工程提供借鉴。陕西水利

[1]陈磊,张土乔,吕谋等.遗传算法优化网络神经元网络模型[J].中国给水排水,2003,（5）5-7.

[2]陈渠昌,郑要全.微灌田间管网支毛管优化设计探讨[J].灌溉排水,1996,（5）:17-21.

[3]董文楚.树状管网布置的优化方法[J].喷灌技术,1984,（4）:25-28.

[4]范业兴,马孝义，康银红等.树状灌溉管网两级遗传优化设计 [J].人民黄河,2007,29（6）:41-43.