压裂油藏导流裂缝多相流动的高效有限差分模型

周方奇，施安峰，王晓宏

（中国科学技术大学热科学和能源工程系）

0 引言

压裂技术作为开发低渗透油藏的有效增产手段已被广泛应用[1-4]。压裂中产生若干条尺度较大的导流裂缝，为准确预测压裂后油藏中的流体流动状况，需采用准确的导流裂缝数值模拟方法。

对于裂缝型油藏，双重介质模型[5-8]已被广泛应用，而含有大尺度导流裂缝的油藏并不满足该模型的使用条件。早期学者们使用单重介质模型模拟导流裂缝，但由于该模型需要极细密的网格描述裂缝和基质，所以计算量很大、效率很低，难以应用到实际的油藏数值模拟中。为了提高计算效率，一些学者提出离散裂缝模型[9-15]，假设N维的系统中裂缝内流体的流动是N−1维的，在划分网格时裂缝节点与基质节点相互重合，并把裂缝及基质方程叠加后进行计算，该模型可较准确地模拟单相流动，但无法应用于多相流动问题。随后一些学者对离散裂缝模型进行了改进[16-19]，使用基于达西定律的交换流量耦合裂缝及基质方程，改进后的模型可以模拟裂缝油藏中的多相流动，但是仍然需要沿着裂缝的走势划分基质网格。Lee等[20-22]提出了嵌入裂缝模型，把裂缝近似地看作基质网格中的井源，采用类Peaceman公式[23-24]计算裂缝与基质网格之间的物质交换，虽然该模型可以提高网格划分的效率，但在多相流动问题中，并不能准确描述裂缝和基质之间的物质交换。

本文考虑基质相饱和度在裂缝两侧的不连续性，提出一种新的嵌入裂缝模型，以期提高计算效率和精度，准确模拟压裂后油藏中的流动状况。

1 数学模型

在人工压裂低渗透油藏中，油藏介质为流体的主要存储空间，其渗透率较低，通常被称为基质。裂缝渗透能力强，成为流体的主要流通通道。本文考虑油水两相流问题，以二维空间为例进行研究。由于裂缝的开度很小，其中流体的流动可以认为是一维的，设裂缝的开度为wf，单位时间内从单位长度裂缝流入基质的α（α=w, o）相流体流量为qα，则裂缝中α相流体的质量守恒方程为：

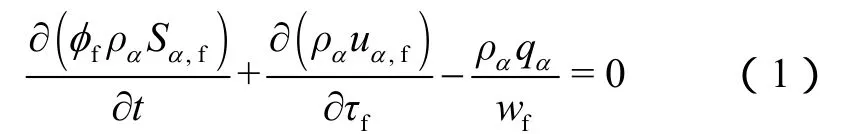
把裂缝看作基质中的源项，基质方程可写作：

其中α相流体的流速满足达西定律：

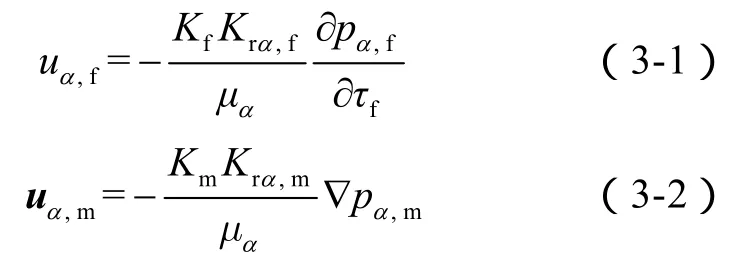
由于裂缝开度很小，基质中的压力场在跨越裂缝时保持连续，但裂缝和基质中多相流体流动特征不同，所以在两者界面处相饱和度发生间断，基质的相饱和度场在越过裂缝时并不连续（见图 1），因此裂缝和其两侧基质的物质交换并不相等，基质与裂缝的交换流量为：

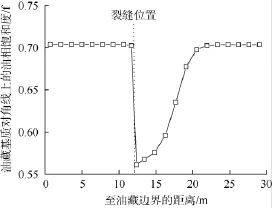
图1 油藏基质对角线（裂缝法向）上的油相饱和度分布曲线

裂缝流入两侧基质的流量qα,1和qα,2满足：

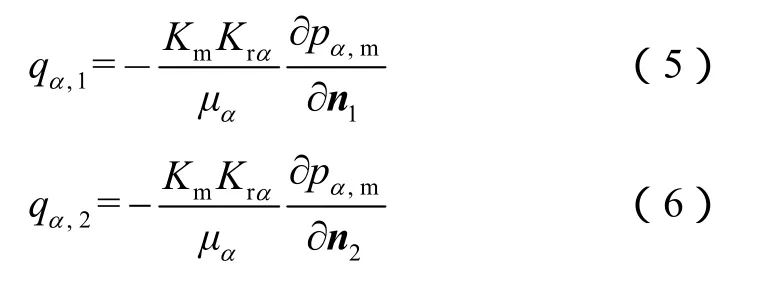
2 控制方程的数值求解

2.1 裂缝及基质的网格划分

对于含有复杂裂缝的油藏，使用不规则网格划分基质系统可以有效地贴合裂缝，但当裂缝分布较为密集时，这类网格的划分过程十分复杂，且工作量巨大。本文使用正交结构网格划分油藏基质，网格的空间步长为 Δx=Δy=1.0 m，将裂缝看作嵌入在基质网格中，这样可以对含有复杂裂缝的油藏进行高效网格划分，以提高模拟效率。

2.2 裂缝网格的计算

嵌入基质的裂缝被规则的基质网格分割为Nf段一维裂缝网格，假设其开度都为wf，取第k段裂缝网格为研究对象，其长度为Lk。由于裂缝内流体的流动被认为是一维的，所以可以使用常规的一维离散格式将（1）式全隐式离散为：

通过裂缝网格2个界面的流速可由下式得到：

对于裂缝与基质之间的流量交换，无法使用常规格式进行离散。本文在裂缝两侧分别建立参考点A和B（见图 2），其位于裂缝网格的垂直平分线上，与裂缝的距离分别为dA和dB。由于压力场在裂缝附近连续分布，且其导数在单侧基质中也保持连续，所以参考点A和B上的压力可以通过裂缝及基质网格中的压力单侧插值予以确定，因此裂缝与两侧基质的流量交换可由下式求出：

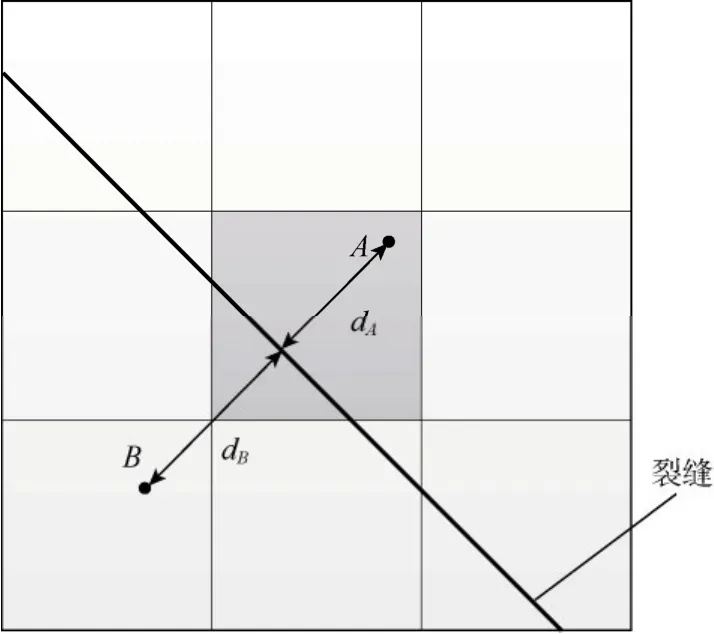
图2 裂缝网格两侧参考点示意图

2.3 基质网格的处理

在油藏中，把空间坐标为（i，j）的网格作为研究对象，使用二维九点离散格式，（2）式可以被全隐式离散为：

其中λα=TKrα,mρα/μα，系数T满足：

利用（12）式可以对常规基质网格进行离散，由于裂缝穿过基质网格，受其影响流体的某些物理量会在网格中发生间断，导致该网格的参数无法准确定义，因此本文在对基质方程进行离散时，这种网格将不参与实际计算，而是为其他网格的计算提供边界条件。由于裂缝两侧基质中压力梯度分别保持连续，可以通过单侧插值的方法由相邻基质网格及裂缝网格中的压力确定被裂缝隔开的两部分基质中的压力分布，然后得到由网格（i，j）进入网格（i－1，j）和（i，j+1）的流量qi－1/2,j和qi,j+1/2（见图 3），从而为网格（i－1，j）和（i，j+1）的计算提供边界条件。同理，该类网格与相邻常规网格的流量交换都可以使用以上的方法求出，因此，图 3中虚线界面可以被认为是整个油藏基质中的内边界，且满足第二类边界条件。

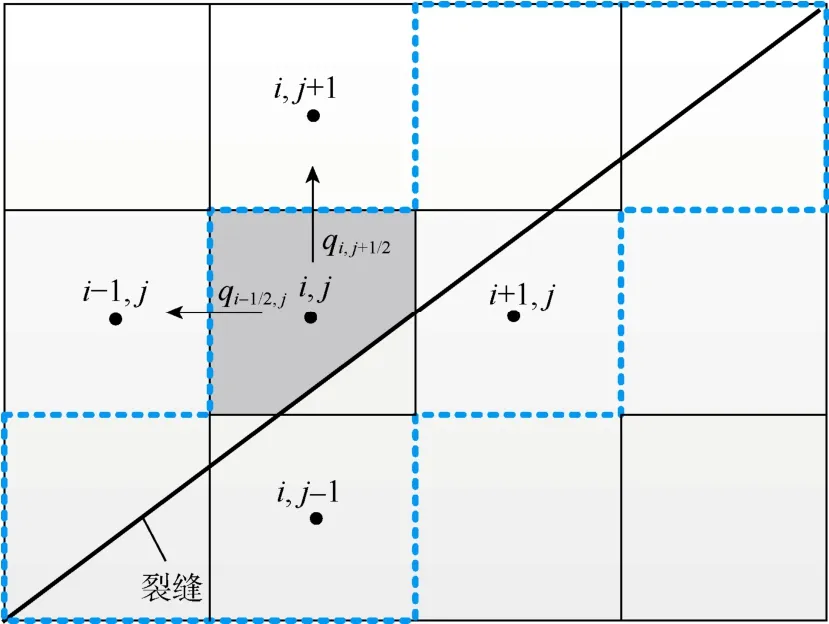
图3 内边界替代覆盖裂缝的基质网格

在求解裂缝控制方程时，若裂缝位于油藏内部，则在两端取绝流边界条件；若裂缝延伸至油藏边界，其两端的边界条件则由油藏的外边界条件确定。

3 算例

本文用 2个算例验证模型的可靠性，并将计算结果与改进后的离散裂缝模型（参考模型）及 Lee的模型进行比较。

首先考虑包含直裂缝（即裂缝与油藏边界正交）的油藏，基质和裂缝的渗透率分别为 1.0 μm2和10 000.0 μm2[22]，注入井和生产井井底压力分别为10 MPa和 7 MPa，油相和水相的初始饱和度分别为 0.7和0.3。开井2 d后，油藏中基质和裂缝的油相饱和度分布情况见图4。可以看出本文模型与参考模型的计算结果基本相同（见图5），这是因为本文模型考虑了裂缝两侧相饱和度的间断，分别计算裂缝与两侧基质的流量交换，所以可以准确地描述裂缝对油藏的影响，得到较精确的结果；而 Lee模型并未考虑裂缝两侧基质流场，所以对交换流量的描述存在误差，从而影响了模拟结果的准确性。

图4 包含直裂缝的油藏开井2 d后油相饱和度分布图

对于含有斜裂缝的油藏，即裂缝与边界并不正交的油藏，假设其中基质和裂缝的渗透率分别为1.0×10−3μm2和20.0 μm2，注入井和生产井井底压力分别为100 MPa和70 MPa[22]，通过数值模拟计算出开井100 d后基质和裂缝中油相饱和度分布情况（见图 6），与直裂缝油藏中的情况类似，无论是在基质中还是在裂缝中，本文模型的结果都与参考结果保持一致，且优于 Lee模型（见图7）。

图5 直裂缝中的油相饱和度分布曲线

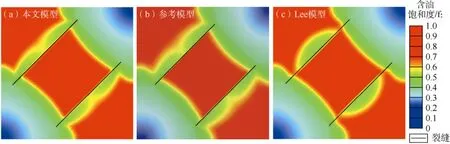
图6 包含斜裂缝的油藏开井100 d后油相饱和度分布图

图7 斜裂缝中的油相饱和度分布曲线

以上计算实例说明，对于油藏中不同形态的导流裂缝，本文模型都可以准确地进行模拟，而且计算精度与改进后的离散裂缝模型相同，高于Lee模型。

4 结论

本文采用规则网格划分油藏区域，裂缝被覆盖在基质网格中，大幅度降低了网格划分难度和计算量；同时考虑到流体相饱和度在裂缝两侧的不连续性，分别计算裂缝和其两侧基质之间的物质交换量；在离散基质方程时，使用内边界替代含有裂缝的基质网格参与计算，有效避免了因这种网格内物理量被模糊定义而产生的误差；算例表明，本文模型可以对含有导流裂缝的油藏进行高效准确的流动模拟。

本文只考虑了独立的裂缝，应对裂缝与裂缝之间的相互交叉与影响作进一步研究。

符号注释：

φ——孔隙度，f；ρ——流体密度，kg/m3；S——流体饱和度，f；um——基质中流体的流速，m/s；uf——裂缝中流体的流速，m/s；q——流量，m3/s；t——时间，s；r——原点到方程控制点的向量，m；τf——裂缝的切向向量，m；τf——裂缝切向向量的模，m；μ——流体的黏度，Pa·s；K——绝对渗透率，μm2；Kr——相对渗透率，f；p——流体的压力，Pa；n——裂缝表面法向向量；Δt——时间步长，s；d——参考点与裂缝的距离，m。下标：α——相，α=w，o；β——介质，β= m，f；m——基质；f——裂缝；0——上时刻的变量；1，2——裂缝的2个表面。

[1]李根生, 盛茂, 田守 嶒, 等.水平井水力喷射分段酸压技术[J].石油勘探与开发, 2012, 39(1): 100-104.Li Gensheng, Sheng Mao, Tian Shouceng, et al.Multistage hydraulic jet acid fracturing technique for horizontal wells[J].Petroleum Exploration and Development, 2012, 39(1): 100-104.

[2]贾承造, 郑民, 张永峰.中国非常规油气资源与勘探开发前景[J].石油勘探与开发, 2012, 39(2): 129-136.Jia Chengzao, Zheng Min, Zhang Yongfeng.Unconventional hydrocarbon resources in China and the prospect of exploration and development[J].Petroleum Exploration and Development, 2012,39(2): 129-136.

[3]黄昌武.页岩油气压裂理论方法和技术体系初步形成[J].石油勘探与开发, 2012, 39(4): 443.Huang Changwu.Theoretical methodology and technical system for shale reservoir fracturing[J].Petroleum Exploration and Development,2012, 39(4): 443.

[4]徐鹏, 程远方, 刘新云, 等.低渗透油气藏爆炸压裂模拟试验及裂缝分形特征[J].石油勘探与开发, 2013, 40(5): 636-640.Xu Peng, Cheng Yuanfang, Liu Xinyun, et al.Explosive fracturing simulation experiment for low permeability reservoirs and fractal characteristics of cracks produced by explosive fracturing[J].Petroleum Exploration and Development, 2013, 40(5): 636-640.

[5]Barenblatt G I, Zheltov I P.Basic flow equations for homogeneous fluids in naturally fractured rocks[J].Doklady Akademii Nauk, 1960,13: 545-548.

[6]Warren J E, Root P J.The behavior of naturally fractured reservoirs[J].Society of Petroleum Engineers Journal, 1963, 3(3):245-255.

[7]Lim K T, Aziz K.Matrix-fracture transfer shape factors for dual-porosity simulators[J].Journal of Petroleum Science and Engineering, 1995, 13(3/4): 169-178.

[8]Kazemi H, Merrill L S, Porterfield K L, et al.Numerical-simulation of water-oil flow in naturally fractured reservoirs[J].Society of Petroleum Engineers Journal, 1976, 16(6): 317-326.

[9]Noorishad J, Mehran M.An upstream finite element method for solution of transient transport equation in fractured porous media[J].Water Resources Research, 1982, 18(3): 588-596.

[10]Baca R G, Arnett R C, Langford D W.Modelling fluid flow in fractured-porous rock masses by finite-element techniques[J].International Journal for Numerical Methods in Fluids, 1984, 4(4):337-348.

[11]Kim J G, Deo M D.Finite element, discrete-fracture model for multiphase flow in porous media[J].AIChE Journal, 2000, 46(6):1120-1130.

[12]Karimi-Fard M, Firoozabadi A.Numerical simulation of water injection in fractured media using discrete-fracture model and the Galerkin method[J].SPE Reservoir Evaluation & Engineering, 2003,6(2): 117-126.

[13]Kim J G, Deo M D.Comparison of the performance of a discrete fracture multiphase model with those using conventional methods[R].SPE 51928, 1999.

[14]Monteagudo J, Firoozabadi A.Control-volume method for numerical simulation of two-phase immiscible flow in two- and three-dimensional discrete-fractured media[J].Water Resources Research, 2004, 40(7):1-20.

[15]Monteagudo J, Firoozabadi A.Control-volume model for simulation of water injection in fractured media: Incorporating matrix heterogeneity and reservoir wettability effects[J].Society of Petroleum Engineers Journal, 2007, 12(3): 355-366.

[16]Slough K J, Sudicky E A, Forsyth P A.Numerical simulation of multiphase flow and phase partitioning in discretely fractured geologic media[J].Journal of Contaminant Hydrology, 1999, 40(2):107-136.

[17]Slough K J, Sudicky E A, Forsyth P.A.Grid refinement for modeling multiphase flow in discretely fractured porous media[J].Advances in Water Resources, 1999, 23(3): 261-269.

[18]Karimi-Fard M, Durlofsky L J, Aziz K.An efficient discrete-fracture model applicable for general-purpose reservoir simulators[J].Society of Petroleum Engineers Journal, 2004, 9(2): 227-236.

[19]Sandve T H, Berre I, Nordbotten J M.An efficient multi-point flux approximation method for discrete fracture-matrix simulations[J].Journal of Computational Physics, 2012, 231(9): 3784-3800.

[20]Lee S H, Jensen C L, Lough M F.An efficient finite difference model for flow in a reservoir with multiple length-scale fractures[J].Society of Petroleum Engineers Journal, 1999, 5(3): 268-275.

[21]Li L, Lee S H.Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media[J].SPE Reservoir Evaluation & Engineering,2008, 11(4): 750-758.

[22]Moinfar A, Narr W, Hui M H, et al.Comparison of discrete-fracture and dual-permeability models for multiphase flow in naturally fractured reservoirs[R].SPE 142295, 2011.

[23]Peaceman D W.Interpretation of well-block pressures in numerical reservoir simulation[J].Society of Petroleum Engineers Journal,1978, 19(3): 183-194.

[24]Peaceman D W.Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability[J].Society of Petroleum Engineers Journal, 1983, 23(3):531-543.