复杂地质条件下水工隧洞的开挖与支护模拟
2014-07-25郝立宪
郝立宪
(宝鸡峡引渭灌溉管理局兴平总站配水站 陕西 兴平 713100)
目前,国内外正大规模的进行水利工程项目的建设,一大批的水电站、供水工程、农田灌溉工程正在施工实施。在这些项目的实施过程中,往往由于施工导流或输水的需求而需要用到水工隧洞这种水电工程中常见的建筑物型式。但是由于受水利工程枢纽布置及场地的限制,水工隧洞的洞线选择受到限制,水工隧洞常常需要穿过各种不良的地质段,如软弱夹层、断层及破碎带等。这些不良地质段通常是制约整个工程进度、制约隧洞施工工期以及工程安全的关键所在,也是影响工程运行期运行安全的关键。工程中对于这些不良的地质条件,常需对隧洞采取各种加固措施,如锚固支护、增加衬砌厚度等,这些支护手段及支护时机是影响工程安全、投资的核心所在。目前,隧洞的施工常采用新奥法施工,在此种施工方法下,隧洞开挖后立即进行支护,隧洞的初期支护是其最终衬砌的一部分。这种施工方法与传统的矿山法施工的主要区别在于矿山法施工是将初期支护作为临时的设施,在衬砌完成后进行拆除,而新奥法主要是采用锚杆、挂网喷射混凝土的方式,将隧洞周围围岩与喷射支护形成一个统一的受力体,达到共同受力、共同变形的目的。
对于隧洞的支护形式设计,目前主要依靠工程类比的方法确立初步的支护方案,同时结合施工过程中监测数据进行分析,以便适时的调整支护方案。随着数值分析理论以及各种岩土体本构的发展,采用各种数值分析手段对隧洞的开挖过程及支护形式进行模拟分析也得到广泛的应用,如有限单元法、有限差分等。本文以云南省某供水工程为例,采用有限元软件SIGMA/W对该隧洞的施工过程及支护方式进行模拟研究,旨在论证该工程支护方式的合理、可靠性。
1 隧洞开挖与支护模拟的基本理论
本文采用有限元软件SIGMA/W对隧洞开挖过程及支护进行应力变形分析。SIGMA/W是解决二维平面应变或轴对称问题的方法,采用小变形或小应变理论解决此类问题。SIGMA/W中对于一个给定的时间增量,有限元方程表示如下:

式中,[B]——应变-位移矩阵;
[C]——本构关系矩阵;
{a}——节点增量的x、y位移列向量;
〈N〉——插值函数的行向量;
A——沿单元边界的面积;
v——单元体积;
b——单位体力强度;
p——增加的表面压强;
很多学者对创新创业的概念进行了内涵阐释和溯源追踪。目前关于创新创业教育所形成的共识是指学生充分运用其所掌握的知识、技能、信息和机会等资源,以创新的思维实现目标,从而达到培养学生可持续发展素质的目的。但其中仍然存在着很多需要改进的地方,包括高校、社区、企业、学生、教师等在内的各方行动主体对创新创业仍然存在认识不一致、认知不全面的误区和偏差,如认为创新创业仅是为了应对就业压力的权益之举,创新创业仅是社区短期培训或是高校就业创业指导中心的职责,等等。
{Fn}——集中节点增加荷载。
对于二维平面应变问题,认为所有的单元都是单位厚度,对常单元厚度t,上述方程可写为:
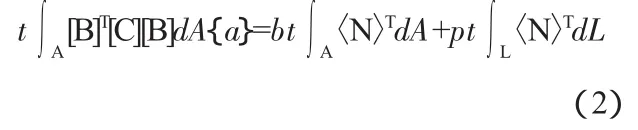
有限元方程的简化形式为:
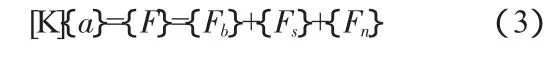
式中,[K]——刚度矩阵,[K]=tA∫[B]T[C][B]dA;
{a}——节点位移增量;
{F}——施加的节点力,由三部分组成;
{Fb}——体积力增量;

{Fn}——节点集中力增量。
对于每个时间增量步求解上述有限元方程,得到位移增量,并求解相应的增量应力和应变,把从第一个增量步以来的增量累加起来,就可得到总应力及变形。
隧洞锚杆支护采用SIGMA/W中杆单元模拟,通过如下几个参数来模拟锚杆的加固作用:弹性模量(E-Modulus)、横截面面积(Area)、起作用时间步(Active Step)、预应力(Pre-force)、施加预应力时间步(App.Step=step toapply pre-force)等。
2 工程概况
云南省昆明市某引水供水工程是该省重点工程项目,其中Ⅲ标段隧洞地处于云南省昆明市禄劝县境内。隧洞全长1286.106m,海拔高度2000m以上,出口段埋深10m~30m,属浅埋隧洞。根据图纸,原设计Ⅴ类围岩长度165m,在实际开挖过程中,全部为全风化的板泥岩,节理发育并切割成碎石,节理缝有土填充,从其石质分析尚不够Ⅴ类围岩的标准,属于不良地质地段。根据图纸设计,Ⅴ类围岩的开挖无超前预支护,光面爆破,开挖后支护采用2m锚杆间距1.5m梅花形布置、拱部挂φ6钢筋网、喷C25砼厚8cm,边墙素喷C25砼8 cm。但是在实际施工过程中,鉴于围岩情况,原设计的支护方案不能保证施工安全。对此,必须对支护方案进行调整,采用钢支撑挂网喷砼的强支护方案。钢格栅间距洞口10m内每0.5m一榀,其它地段间距为0.5m~1.0m,钢格栅定位采用Φ22径向锚杆,锚杆长2m,每榀在墙脚、拱脚和拱腰各设一根,格栅间采用Φ22钢筋连接,间距0.5m,格栅背后挂钢筋网,网格间距2.5cm×2.5cm,最后喷C25砼厚15cm。
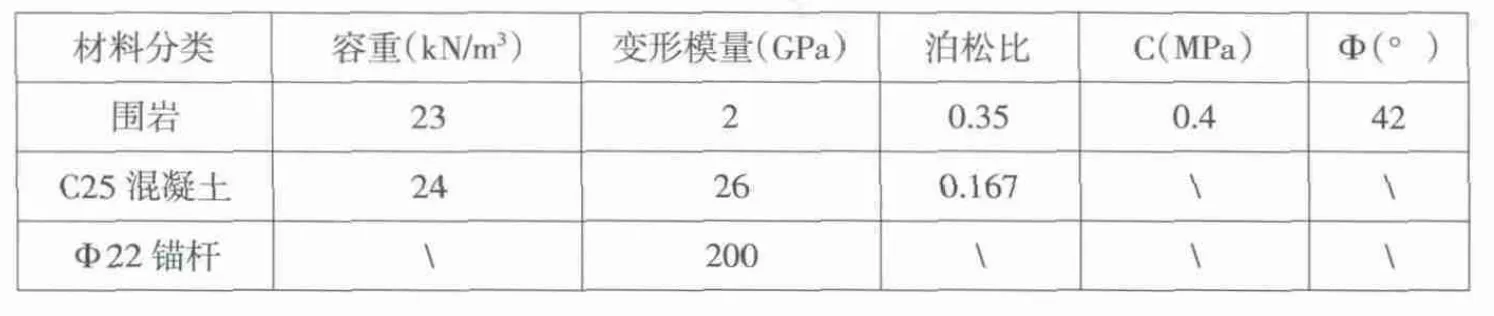
表1 材料计算参数表
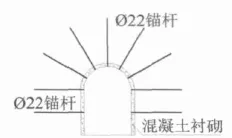
图1 隧洞支护及衬砌示意图
图2 计算模型示意图

图3 两种工况下第一步开挖后水平及竖向位移云图

图4 两种工况下第二步开挖后水平及竖向位移云图
3 有限元模型及计算结果
3.1 计算参数及模型
本例中隧洞为城门洞型无压输水隧洞,洞宽为2m,洞高为3.5m。模型计算范围取为:隧洞左右两侧取10倍的洞宽,洞顶以上取至原始地面(设隧洞埋深为最大值30m),洞底以下取1倍的洞高。隧洞围岩在开挖过程中可能产生塑性变形,因此采用理想弹塑性本构模型,屈服准则采用莫尔库伦准则;喷射混凝土刚度较大,支护后变形较小,因此采用弹性模型。计算两种不同的工况:①原设计的开挖支护方案,即深2mΦ22锚杆间距1.5m梅花形布置+8cm厚C25砼喷护;②施工改进方案,即2mΦ22锚杆间距1.5m梅花形布置+15cm厚C25砼喷护。计算中假定分两步开挖和支护,首先挖除拱顶部分同时打入锚杆并喷射混凝土,在上层施工完成后再开始挖除以下部分,打入锚杆并喷射混凝土。各种材料计算参数如表1所示。
3.2 计算结果
计算中首先进行原位初始地应力场分析,此时隧洞未开挖,整个断面均为围岩,计算出的竖向地应力场呈三角形分布。在初始地应力场计算结果的基础上进行第一步的开挖计算,选择Load/Deformation即加载变形分析类型,挖除拱顶的岩石,包含即将衬砌部分,同时激活拱顶的7根锚杆以及衬砌层的混凝土。提取开挖第一层后的隧洞水平向及竖直向的位移,如图3所示。
在完成拱顶的开挖后紧接着模拟直墙段的开挖与支护,与第一步的开挖支护模拟过程相同,首先移除隧洞直墙段的岩石,包含即将衬砌部分,同时激活直墙段的2根锚杆以及衬砌层的混凝土。提取开挖支护完成后的隧洞水平向及竖直向的位移,如图4所示。
4 结论与讨论
从上述计算结果可以看出,原设计支护方案在第一步开挖结束后,其水平位移发生在开挖面拱脚下侧,最大位移0.14mm,两侧呈对称分布。拱顶部位置左侧位移为正,右侧位移为负;开挖面两侧边墙左侧位移为负,右侧位移为正;开挖面以下左侧位移为正,右侧位移为负;改进后方案的水平位移与原设计方案位移分布规律一致,水平位移最大值相当,均为0.14mm。第一步开挖后,原设计支护方案的竖向位移呈现拱顶向下变形,拱底向上凸起的形态。原设计方案拱顶向下的最大位移为0.28mm,底部向上凸起最大位移为0.65mm;改进后方案竖向位移分布与原设计方案分布规律一致,只是竖向位移有所减少,拱顶的最大位移为0.24mm,拱底的最大位移为0.62mm。
整个开挖结束后,原设计方案水平向最大位移发生在直墙段下侧,最大位移为0.44mm,左右对称分布,左侧位移为正,右侧位移为负;改进后方案开挖完成后的水平位移分布规律与原设计方案相同,最大水平位移为0.41mm。原设计方案竖向位移分布表现为拱顶向下变形,拱底向上凸起的形态。原设计方案的拱顶最大位移为0.28mm,改进后方案拱顶的最大位移为0.24mm,相比原设计方案竖向位移有所减小,说明改进方案具有一定的合理性。同时通过上述计算分析,可以得出如下结论:
(1)隧洞开挖过程中随着开挖进程的推进,隧洞周围围岩变形逐渐增大,且初始开挖时的变形最大,随着施工的推进,后续变形逐步减小。
(2)隧洞开挖后,水平向位移变化呈现明显的对称分布规律,且两侧位移方向相反。
(3)隧洞开挖后,竖直向位移变化呈现拱顶向下变形(且一般为隧洞变形最大的部位),隧洞底部向上凸起的现象。陕西水利
[1]肖明.地下洞室施工开挖三维动态过程数值模拟分析[J],岩土工程学报,2000,22(4):421-425.
[2]程良奎,扬志银.喷射混凝土与土钉墙[M].北京:中国建筑工业出版社,2001.
[3]李世辉.隧道围岩稳定性系统分析[M].北京:中国铁道出版社,1991,7~8.
[4]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,1998.
