离散Markovian跳变系统模态依赖非脆弱H∞控制

冉华军 肖 鹏

（三峡大学 电气与新能源学院，湖北 宜昌 443002）

H∞控制是一种优化控制，是以控制系统内部某些信号之间传递函数矩阵的H∞范数作为优化性能设计指标的优化控制，反馈控制器不仅要保证闭环系统稳定，并且还要使得闭环系统传递函数的H∞范数小于某一预先设定的正值.Keel等在文献［1］中根据实例指出，传统的最优和鲁棒控制器设计由于忽略了控制器参数的微小摄动往往会导致原来稳定的闭环系统失去稳定或稳定性能下降.Dorato对此进行了进一步研究，得出控制器的脆弱性问题是关系到反馈控制系统性能的基本问题的结论［2］.文献［3］针对无法获取跳变参数的情形，研究了离散Markovian跳变系统模态不依赖非脆弱H∞控制问题.然而，如果跳变系统的当前所处模态实时在线可测，则设计控制器时可以充分利用系统的模态跳变信息.本文针对可获得跳变参数的情况，研究离散Markovian跳变系统模态依赖非脆弱H∞反馈控制问题.

1 问题描述

所研究的离散Markovian跳变系统可描述为［3］：

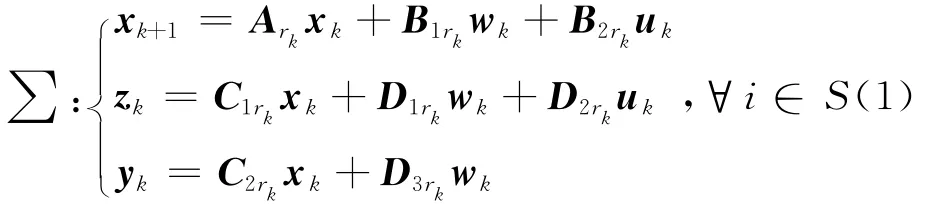
式中，｛rk；k＝0，1，…，∞｝为在有限集合S＝｛1，…，s｝内取值的离散平稳 Markovian链，S包含系统（1）的所有可能跳变模态.假设可直接测量系统状态，且实时可测系统所处模态.对系统（1）设计如下模态依赖反馈控制器：

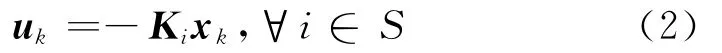
其中Ki为待定控制器增益.

考虑控制器实现时或实际运行中其增益存在不确定摄动Δi，则实际控制器为：

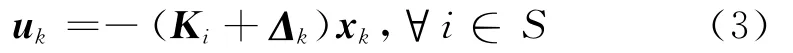
将式（3）代入式（1）得到：

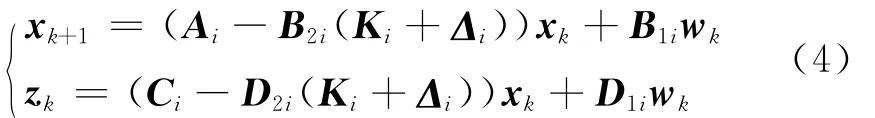
假定待设计控制器（3）的增益存在乘性范数有界不确定摄动，即

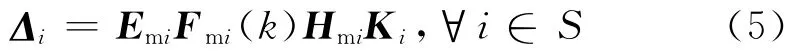
其中Emi，Hmi为适维实常矩阵，Fmi（k）为时变不确定矩阵并满足：

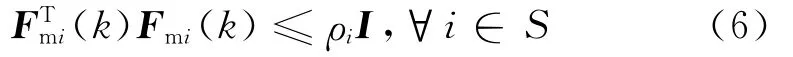
其中ρi为已知正标量.

将（5）和（6）代入（4），得实际闭环系统（7）：

模态依赖非脆弱状态反馈H∞控制问题可归结为：给定常数γ＞0，设计模态依赖非脆弱反馈控制器（3），使得闭环系统（4）对控制器增益摄动均满足：外扰wk＝0时，闭环系统（4）内部均方稳定；零初态时，闭环系统（4）达到γ水平H∞性能，即：‖zk‖＜γ2·‖wk‖.

2 非脆弱H∞控制器设计

由文献［4］中引理，闭环系统（7）内部随机均方稳定且具有γ水平H∞性能的充要条件是，存在适维矩阵Pi＞0，i＝1，…，s，使下列矩阵不等式组成立：

由Schur补引理［5］，式（8）等价于下式：

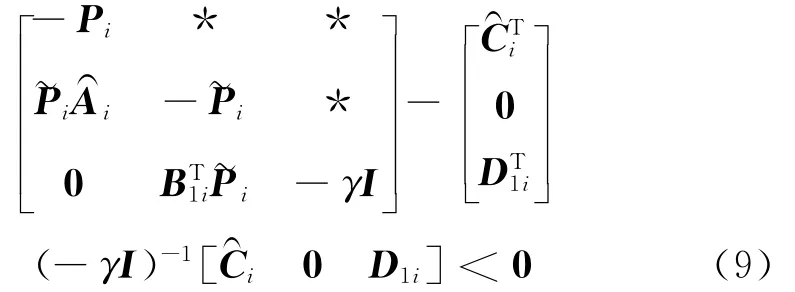
经简单计算和整理且令

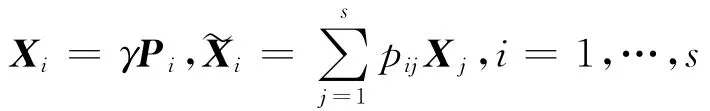
则式（9）等价于：

再由Schur补引理，式（11）等价于：

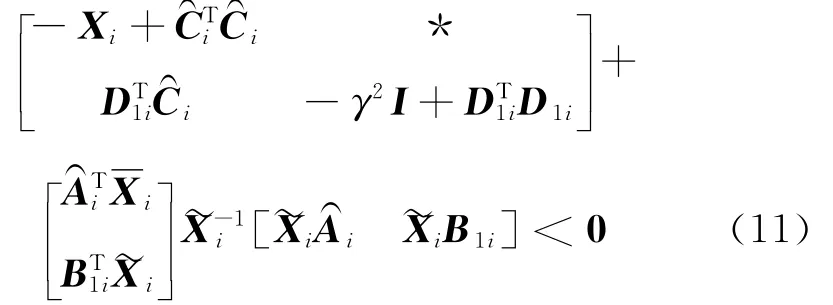
经整理计算，式（11）等价于：

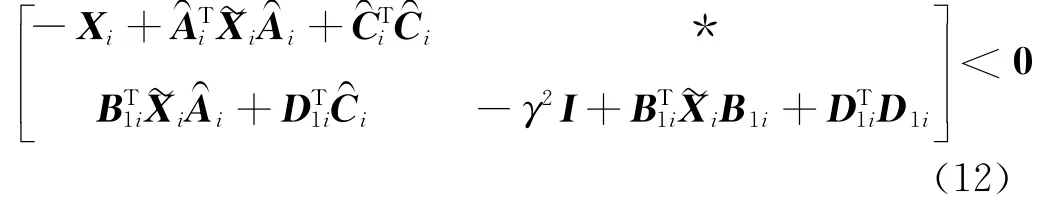
进一步，用矩阵diag｛，I｝及其转置阵对式（12）进行合同变换，式（12）便等价于

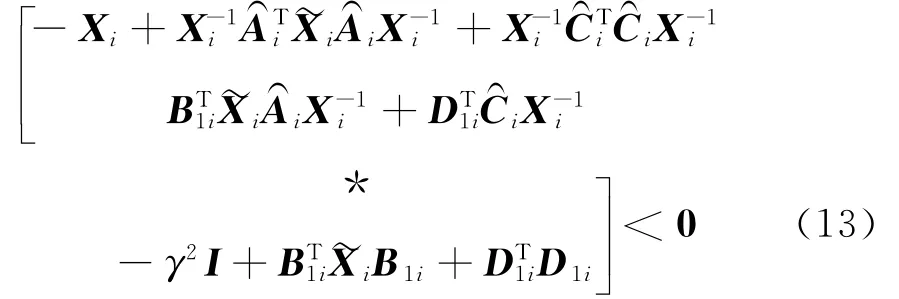
即

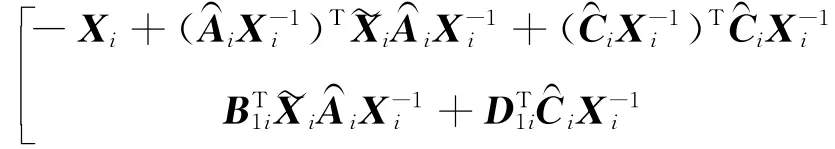
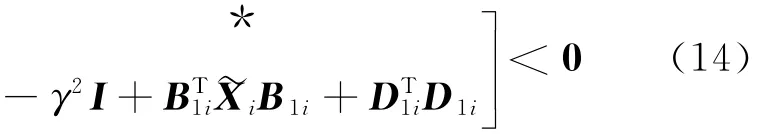
：将式（7）代入（14），并令Wi＝X－1i，Yi＝KiWi，得

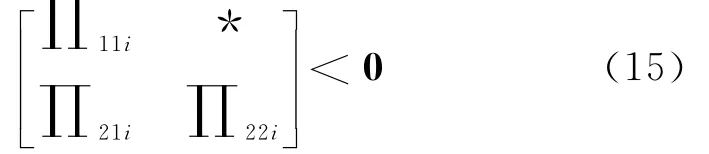
其中：

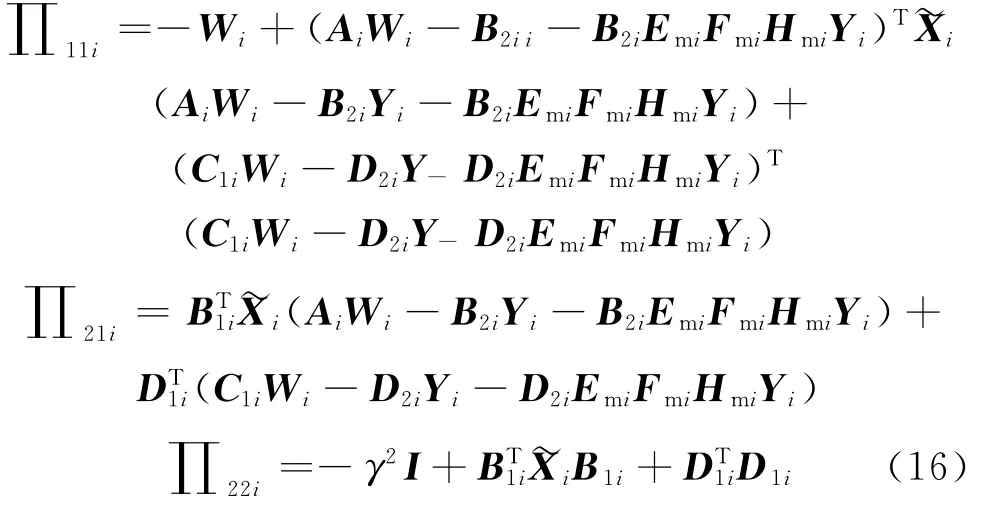
容易看出，式（15）等价于：

进一步，式（17）又可等价于：

再由Schur补引理，式（18）等价于下式：

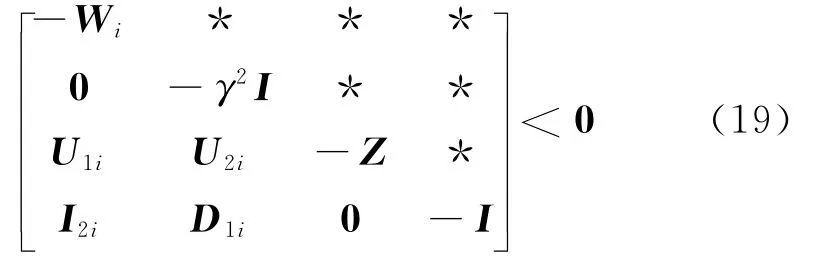
根据矩阵运算法则将不确定项拆分，式（19）又可等价地写为：

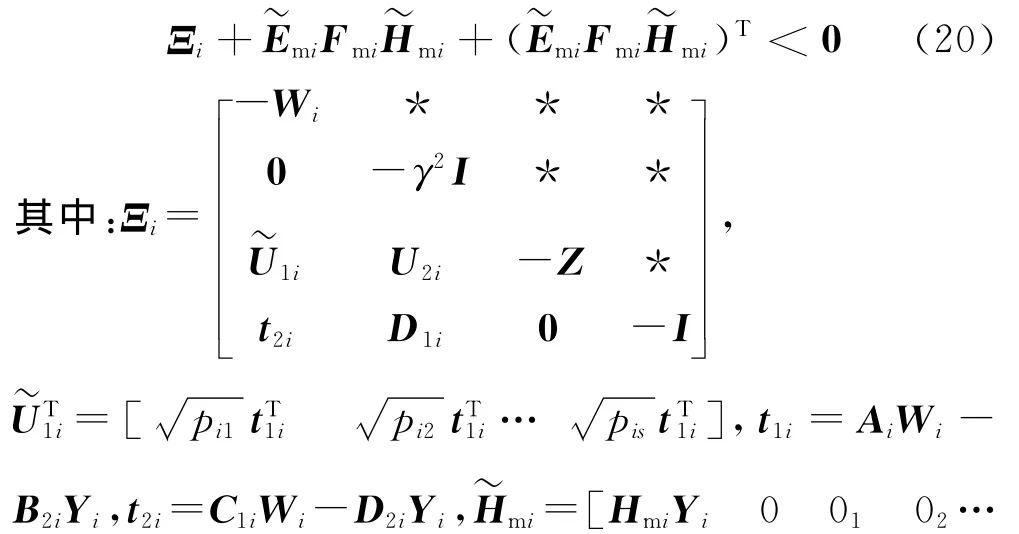
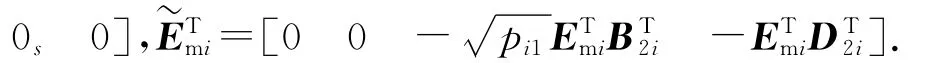
由文献［6－7］中引理，式（20）等价于：

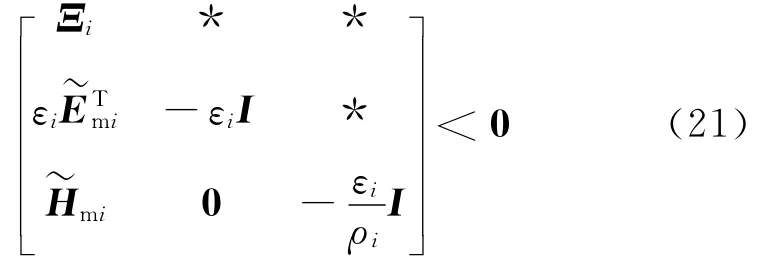
由以上分析，可得如下定理：

定理 当且仅当存在适维矩阵Wi＞0，Yi及正标量εi，i＝1，2，…，s，使矩阵不等式组（21）成立时，离散Markovian跳变系统（1）存在模态依赖非脆弱状态反馈H∞控制器（3），使闭环系统（7）对所有满足式（5）、（6）的乘性范数有界不确定容许控制器增益摄动都保持内部随机均方稳定且具有给定的H∞性能γ，控制器参数为

注释 基于式（22），令ρ＝γ2，通过建立和求解优化问题：

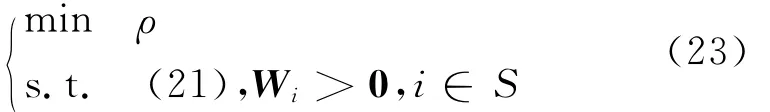
根据定理1，若该优化问题的解存在，则利用最优解可得系统（1）的模态依赖非脆弱最优H∞控制器，相应的最优H∞性能水平为.

3 数值算例

已知一个具体的三模态离散Markovian跳变系统：

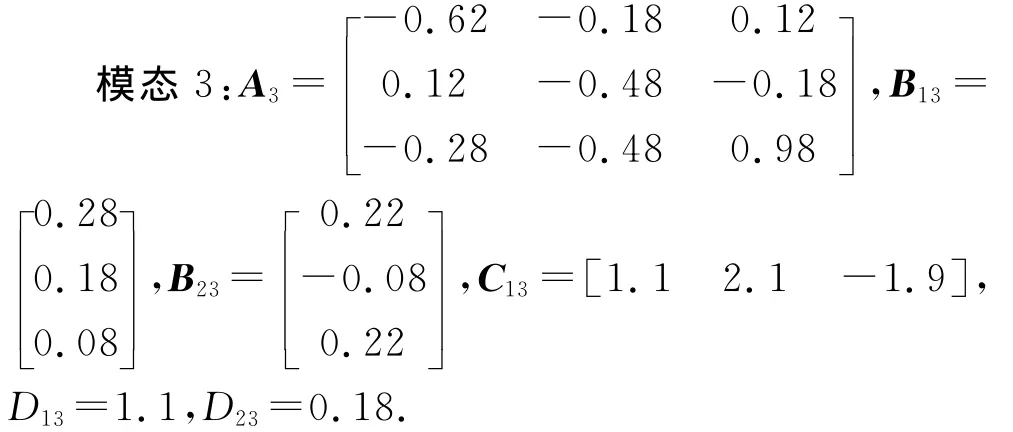
转移概率矩阵：

根据定理1、注释1所描述的方法，在Matlab7.0平台上基于LMI工具箱编写针对γ寻优的求解程序，运行结果为：γopt1＝1.727 9.

控制器增益为：

按常规H∞控制理论设计控制器时，预先未考虑控制器可能出现的摄动.为了凸显本文所提方法的有效性，直接给出按常规H∞控制理论对本算例的设计结果以方便比较：最优H∞性能水平γopt2＝1.719 5；

控制器增益：

若所设计控制器增益在实现时发生了乘性范数有界摄动Fm1＝0.031，Fm2＝－0.031，Fm3＝0.031，容易验证该摄动满足：

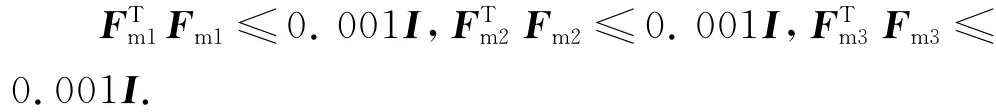
则实际控制器增益为：

可编写程序求出实际控制器使系统所能达到的最优H∞性能水平：γopt3＝1.735 7.

算例结果表明，γopt3＞γopt2，γopt3＞γopt1，若控制器增益发生允许范围内的乘性范数有界摄动，按常规控制理论设计的鲁棒控制器使系统所能达到的实际最优H∞性能水平下降，而按本文设计的非脆弱控制器始终能使系统保持在期望的最优H∞性能水平.

假定系统初态x（0）＝［1.3 2 －0.8］，初始模态r0＝1，w（k）＝0.图1为仿真时三态离散 Markovian链；图2为非脆弱控制器没有发生摄动时状态响应曲线；图3为非脆弱控制器发生摄动Fm1＝0.03，Fm2＝－0.03，Fm3＝0.03时的响应曲线.

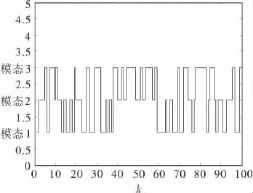
图1 三态离散Markovian链

图2和图3表明，按本文定理1设计的控制器在允许范围内其增益无论摄动与否，闭环系统均稳定.多次改变初态值进行仿真，均可得一致结论.

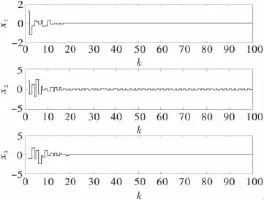
图2 控制器增益未摄动时状态响应

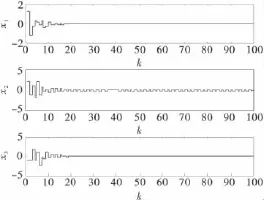
图3 控制器增益摄动时状态响应

假定零初始状态，初始模态r0＝1，图4为系统所受扰动；图5为三模态离散Markovian链；图6为控制器增益未摄动时输出响应；图7为控制器增益发生摄动Fm1＝0.03，Fm2＝－0.03，Fm3＝0.03时非脆弱控制输出响应.

利用norm指令可求得

多次改变扰动信号进行仿真，均可得一致结果.这表明按本文定理设计的非脆弱控制器在允许范围内其增益无论摄动与否，系统H∞性能保持在期望水平.

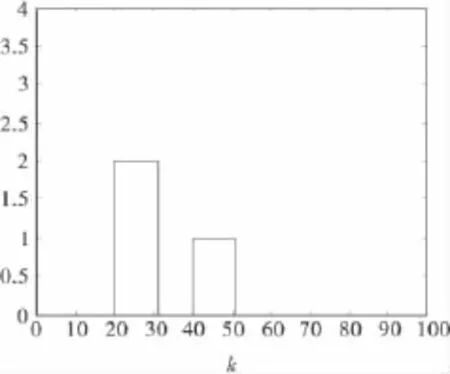
图4 扰动信号

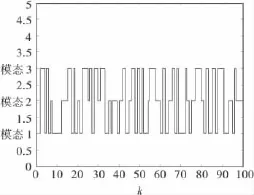
图5 三态离散Markovian链

图6 控制器增益未摄动时输出响应

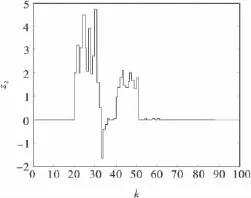
图7 控制器增益摄动时输出响应

4 结 论

本文考虑控制器增益发生乘性范数有界摄动的情形，针对一类跳变参数可获取的线性离散 Markovian跳变系统，运用LMI方法推导出存在使其随机均方稳定且具有H∞性能水平γ的非脆弱H∞反馈控制器的充要条件，并给出了确定控制器增益的显性计算式；最后将本文的理论方法应用于一个具体算例，通过观测分析仿真得到的状态响应和输出响应曲线，并与不考虑控制器增益摄动的常规H∞反馈控制器设计方法的结果相比较，展示了本文方法的可行性和有效性.

［1］ Keel L H，Bhattacharyya S P.Robust，Fragile，or Optimal？［J］.IEEE Transactions on Automatic Control，1997，42（8）：1098－1105.

［2］ Dorato P，Non－fragile Controller Design：An Overview［C］.In：Proceedings of the American Conference，Philadelphia，Pennsylvania，June，1998，5：2829－2831.

［3］ 冉华军.离散 Markovian跳变系统模态不依赖非脆弱H∞控制［J］.三峡大学学报：自然科学版，2012，34（5）：85－91.

［4］ Costa O L V，do Val J B R.Full InformationH∞Control for Discrete－Time Infinite Markov Jump Parameter Systems［J］.Journal of Mathematical Analysis and Applications，1996，202（2）：578－603.

［5］ Kreinder E，Jameson A.Conditions for Nonnegativeness of Partitioned Matrices［J］.IEEE Transaction on Automatic Control，1972，17（1）：147－148.

［6］ Peterson I R.A Stabilization Algorithm for a Class of Uncertain Linear Systems［J］.Systems ＆ Control Letters，1987，8（4）：351－357.

［7］ Xie L H.Output FeedbackH∞Control of Systems with Parameter Uncertainty［J］.International Journal of Control，1996，63（4）：741－750.