基于参考DEM的机载InSAR定标方法

云 烨，曾琪明，2，焦 健，梁存任，王 庆，周 晓

1.北京大学 遥感与地理信息系统研究所，北京 100871；2.北京大学 空间信息集成与3S工程应用北京市重点实验室，北京 100871

1 引 言

机载干涉合成孔径雷达（interferometric synthetic aperture radar，InSAR）主要应用于地形测绘，获取地面的数字高程模型（digital elevation model，DEM）。系统参数误差会影响机载InSAR生成DEM的精度，利用干涉定标校正系统参数对系统误差进行补偿是提高生成DEM精度的关键技术之一［1］。伴随着DEM精准性需求的提高，InSAR定标技术也在逐步发展和完善。目前常用的方法是基于敏感度方程的定标［2－4］，一些学者改进了原有模型，利用InSAR三维重建模型和敏感度方程进行干涉定标［5－8］。在定标中，通常需要布设一定数量的角反射器等人工靶标作为地面控制点（ground control point，GCP）并精确测量其位置，由于角反射器在图像中易识别、具有较准确的地面坐标，与干涉生成DEM中的位置进行比较可得到目标位置偏差［9－10］。而在实际定标中，角反射器需要专门定制；地面布设数量有限，分布受环境限制；布设前需要进行详细的踏勘，野外布设和测量工作量大，尤其在地形复杂的区域布设更为困难；野外飞行试验存在各种不可控原因，导致实际的飞行与设计可能不同，使布设的角反射器失效等。这些可能的情况会给干涉定标带来很大的困难甚至使定标无法进行。

本文提出一种无人工靶标干涉定标方法，利用已知高程精度的参考DEM与待定标InSAR系统生成的DEM进行比较实现干涉参数的标定，该方法类似于光学遥感中的交叉定标，即利用标定好的遥感器与待定标遥感器在相同条件下观察同一地物，通过对比计算得出待定标遥感器的定标系数［11］，这种方法弥补了场地定标成本较高、定标参数更新周期较长的不足。此外，许多针对国内研制的InSAR系统进行的研究都基于仿真试验［4，12－14］，而实际中试验区自然环境、平台稳定性等都有很多不确定因素，这是仿真试验很难模拟的。在精度检验方面，以往研究采用角反射器等作为检验点，通过测量其真实坐标并与定标后的坐标对比来进行误差检验［15］，但是检验点的数量有限、分布也受自然环境的限制［9，15］。本文对无控制点的干涉定标方法进行了试验研究，采用将整个试验区得到的高程数据和参考DEM做差的方法进行精度检验，最后对定标的精度和误差进行了统计分析。

2 基于参考DEM的干涉定标方法与流程

干涉定标主要有3个关键环节：敏感度方程的构建、GCP坐标的获取和敏感度方程的解算。本研究针对后两个环节进行了改进。在目标三维重建模型的基础上构建敏感度方程，方程中的位置误差矩阵通过无人工靶标的干涉定标方法来确定。借助参考DEM模拟SAR图像，将模拟图像与真实图像进行匹配，获得两幅图像的转换关系，得到一系列匹配点（作为GCP）的坐标，它与干涉生成DEM中相应点之间的坐标差构成位置误差矩阵，再利用敏感度方程解算定标参数。在敏感度方程解算时，考虑到各参数测量值和实际值存在偏差对迭代收敛的影响，利用牛顿下山法对敏感度方程解算进行了改进。定标处理流程如图1。

2.1 敏感度方程的构建

基于敏感度方程的定标通过敏感度方程建立高程偏差和各干涉参数偏差之间的关系，用方程组求解的方法对各干涉参数偏差进行估计，利用这一估计值对干涉参数偏差进行校正［1－5］。文献［1，8］基于InSAR测量原理构建了三维重建模型，本文采用文献［1］中的表述，三维重建模型包括InSAR的距离方程、多普勒方程和干涉相位方程

式中，P为目标位置矢量；A1为主天线位置矢量；r1为主天线指向目标的矢量。fdc为多普勒中心频率；λ为电磁波波长为视向方向的单位矢量，v为速度矢量。φ为解缠的干涉相位；b为基线长度；Q为雷达的工作模式（本试验为标准收发模式，Q＝1），在方程展开过程中采用电磁波波前的球面波模型［6］。求解上述3个方程构成的方程组以确定地面目标点的三维位置，求解该方程组的常用方法是视向量正交分解法［1，3，16］，得到目标位置P的表达式［1］如式（4）

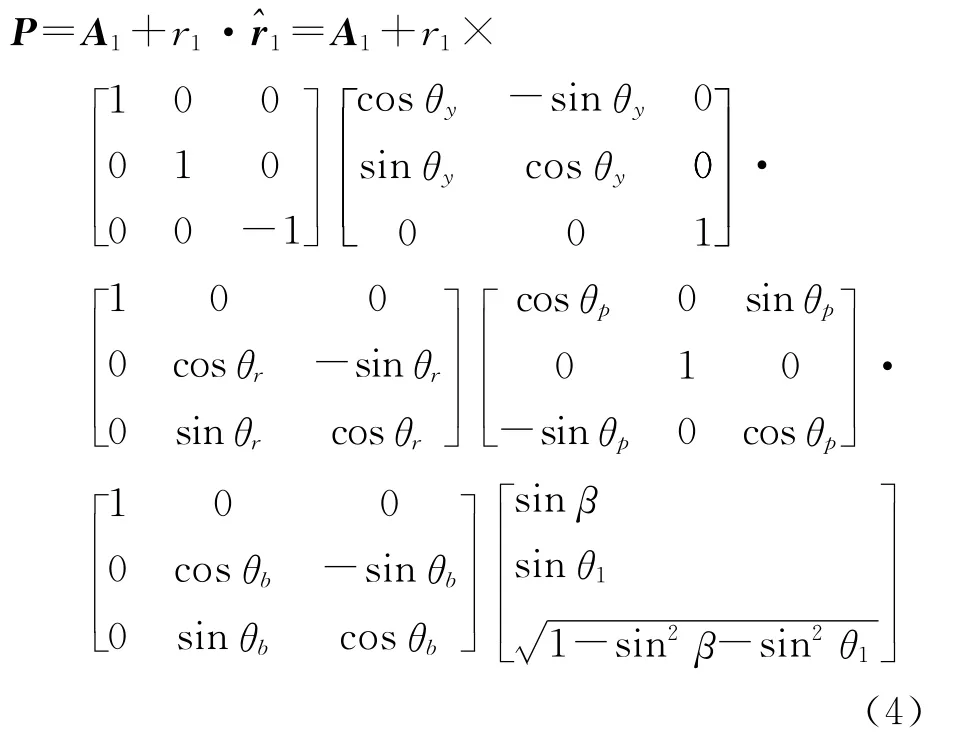
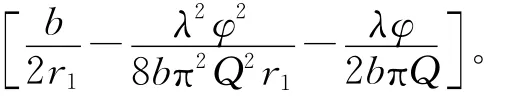
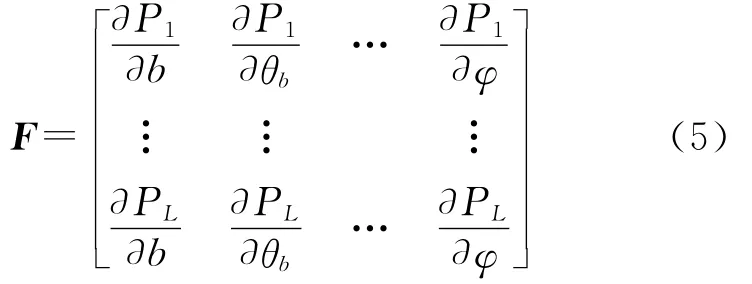
三维位置差和干涉参数偏差的关系构成了敏感度方程

式中，ΔP为L×1阶位置误差矩阵；F为L×N阶敏感度矩阵；ΔX为N×1阶待求的干涉参数偏差向量；N为待定标的参数数目。干涉定标即求式（6）的解ΔX，求解过程可参见文献［1，3，5，8］，其中，F矩阵的结构即干涉定标参数的选择，通过敏感度分析来确定；用无人工靶标的干涉定标方法来得到ΔP。

2.2 基于参考DEM的GCP坐标获取

获取GCP坐标的方法是利用参考DEM（指通过其他方法，如传统测量获得的DEM）模拟SAR图像，建立参考DEM和InSAR生成DEM的关系，获得GCP在两种来源DEM上的坐标差，方法流程如图2。主要包括SAR图像模拟、建立模拟图像和真实图像关系、精度检验等步骤。

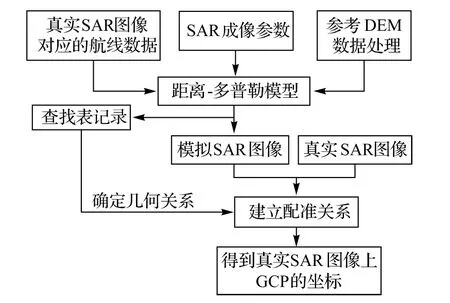
图2 利用模拟SAR图像获取GCP坐标流程图Fig.2 Flow chart of GCP generation by simulated SAR image

2.3 敏感度方程的解算

敏感度方程的解算通常采用广义逆矩阵迭代的方法，其核心思想为最小二乘法。矩阵结构和初始值设置的不同会使敏感度矩阵产生病态，导致得到的偏差改正量并不能使高程误差收敛。研究表明［18］在迭代运算中，初值的选择对迭代过程和结果有很大影响，例如用牛顿法迭代时，若初值偏离所求的根较远，牛顿法可能发散。在敏感度模型解算中，根据系统的初始值进行迭代运算，而初始值一般由实验室测得或飞机惯性导航系统得到，例如基线长度、倾角、飞机姿态角等。由于飞机姿态变化等不确定因素，上述参数测量值与真实值存在一定偏差，例如：雷达天线位置姿态数据通过飞机惯导系统获得，它记录的起始点位于惯导设备中心，而非天线相位中心。另外，常规定标方法中GCP分布不均匀也会造成敏感度矩阵病态。在本研究中，用敏感度模型得到的偏差值修正定标参数重新进行迭代时，得到的结果没有明显收敛，故采用牛顿下山法对定标算法进行改进。

牛顿下山法的基本思想是［18］：为了防止迭代发散，在迭代格式中附加一个条件

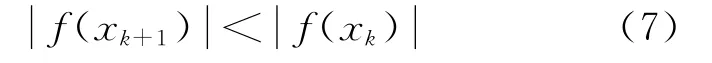
将上述牛顿下山法引入敏感度方程解算中，迭代的附加条件形式与式（7）一致，使其得到的高程差单调下降达到收敛。采用全部试验区得到的高程值与参考DEM做差来检验定标结果，用总体中概率分布最大的高程差值作为衡量指标，即众数M。将式（7）改进为

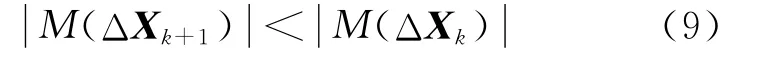
牛顿下山法的f（xk）是一维方程，而在敏感度模型中为多维方程，故将式（8）改进为

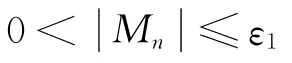
3 试验数据处理与验证

3.1 试验数据

试验数据为中国科学院电子学研究所研制的机载双天线InSAR系统得到的真实数据，主要参数见表1。该系统搭载在无人机平台上（试验时间：2012年9月），试验区位于内蒙古某山区，海拔1400～1800m，主要为山地地形，植被覆盖稀疏，多为荒草，树木极少［19］。试验采用的参考DEM为内蒙古测绘地理信息局生产的1∶1万数字高程模型（生产日期：2008年11月，出版日期：2009年12月），从DEM获取到本研究InSAR数据采集时间间隔内，该地未发生过能够影响地壳运动的重大事件，同时经过和2010年获取的1∶5万DEM比较，两者的趋势一致，而前者是研究区目前可以查询到的分辨率最高的DEM。参考DEM采样间隔（空间分辨率）为5m，山地高程中误差在5m内、高山地在10m内。

表1 InSAR数据主要参数Tab.1 Parameters of InSAR data

3.2 GCP坐标获取

3.2.1 SAR图像模拟

利用参考DEM，基于距离－多普勒模型进行SAR图像模拟［20］，包括几何和辐射模拟。为避免损失数据的细节信息，将参考DEM插值至与SAR图像相同的分辨率1m。经过SAR图像模拟过程，包括：飞行轨道拟合，DEM插值、旋转和镜像，由SAR几何构像模型计算地面点成像位置，建立地面的后向散射模型，计算图像的灰度值等［20］，得到模拟结果如图3（a），真实图像如图3（b）。

3.2.2 建立模拟图像和真实图像的关系获得GCP坐标

由于SAR的侧视成像机理，会产生透视收缩和叠掩等现象，造成SAR图像与参考DEM的点位之间非一一对应，所以在模拟过程中创建一个辅助表记录上述点。同时，创建一个与DEM坐标空间位置对应的查找表，记录每个DEM格网点在模拟图像上的图像坐标；然后建立模拟图像与真实图像精确的仿射变换关系，使模拟图像和真实图像的图像坐标实现互逆转换，同时实现SAR真实图像坐标和查找表信息的对应。通过该方法，使SAR真实图像上每一点以模拟图像为中介都可以对应到参考DEM上，实现GCP坐标的获取及SAR图像的地理编码。

3.2.3 模拟SAR图像精度检验

精度检验包括辐射特征检验和几何精度检验。由于图像具有明显的天线方向图调制效应，辐射特征检验仅作定性分析（图3（a）、（b）），雷达波束照射的前坡较亮，背坡多为弱回波散射区或阴影区，局部纹理变化一致。几何精度检验以真实SAR图像为基准，在模拟SAR图像上进行同名点人工选择，选择特征明显的点（如山脊、山峰点）［20］，如图3（c）。得到31个同名点，如图3（a）、（b），（c）为局部范围的放大图。31个同名点配准均方误差的平均值为0.732像元（其中最大误差1.459，最小误差0.058），像元的大小为1m×1m，表明模拟图像与真实图像之间具有较高的几何相似精度。

图3 模拟SAR图像几何精度检验Fig.3 Registration accuracy of simulated SAR image

3.3 敏感度方程解算及定标

基于参考DEM的无人工靶标干涉定标方法，理论上可以获得图像上全部点的三维坐标。由于SAR原始图像（方位向4096像元／距离向2048像元）两边黑色区域的信噪比较低、相干性较差，故处理中屏蔽两侧的区域。图4为干涉处理和定标使用的GCP在SAR坐标系统下的分布，点的选择原则为在屏蔽两侧区域后均匀分布（距离向间隔50像元、方位向间隔100像元），然后去掉位于SAR图像叠掩、阴影区域的点（3.2.2节中辅助表记录的非一一对应点），得到313个GCP并构建位置误差矩阵。干涉定标参数组合由敏感度分析来确定。通过对基线长度、基线倾角、干涉相位偏置、多普勒中心频率、无人机姿态角、飞行速度等8个变量进行敏感度分析，最后确定的定标干涉参数有：基线长度、基线倾角、干涉相位偏置（式（5）），其敏感度方程表达式由式（4）求微分得到，以基线长度的敏感度为例，公式如下

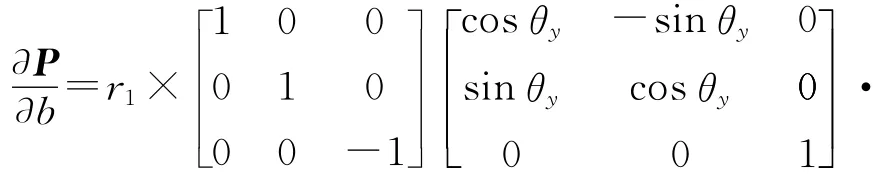
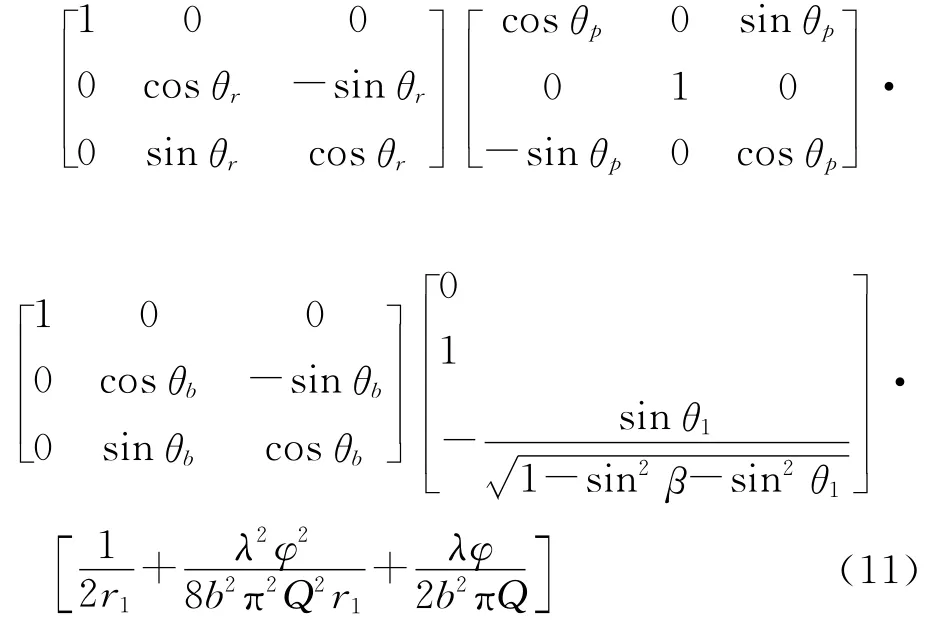
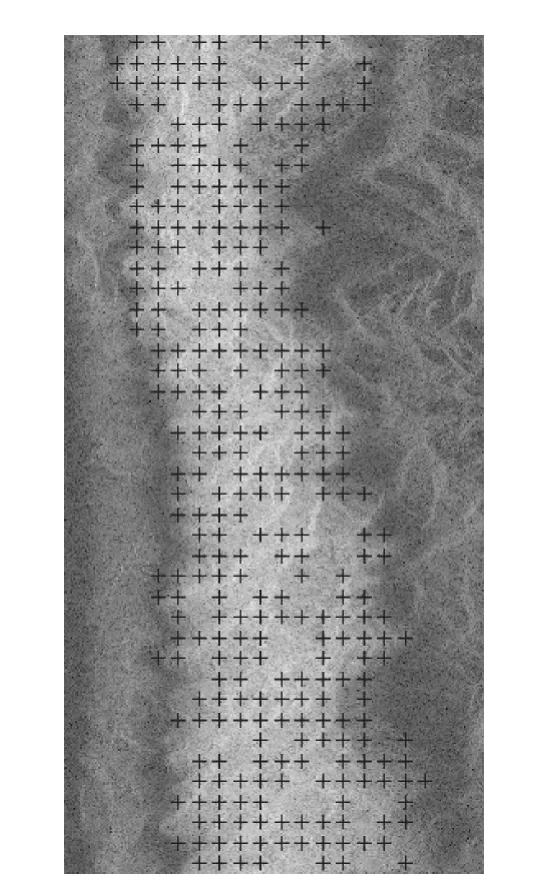
图4 GCP分布图Fig.4 Distribution of GCPs

无人机飞行姿态的不稳定造成垂直基线在方位向上存在变化，根据敏感度分析的结果，垂直基线的变化对高程影响很大，在基线初始值存在误差的情况下，很难仅靠定标来改进这一参数，所以在干涉定标前先对垂直基线进行修正，对其在方位向上做拟合（图5），由图5可知，由于飞机姿态的不稳定，垂直基线沿方位向存在变化趋势，故将基线的改正耦合在干涉处理和定标中，在两个过程中都对基线进行修正。

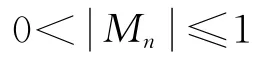
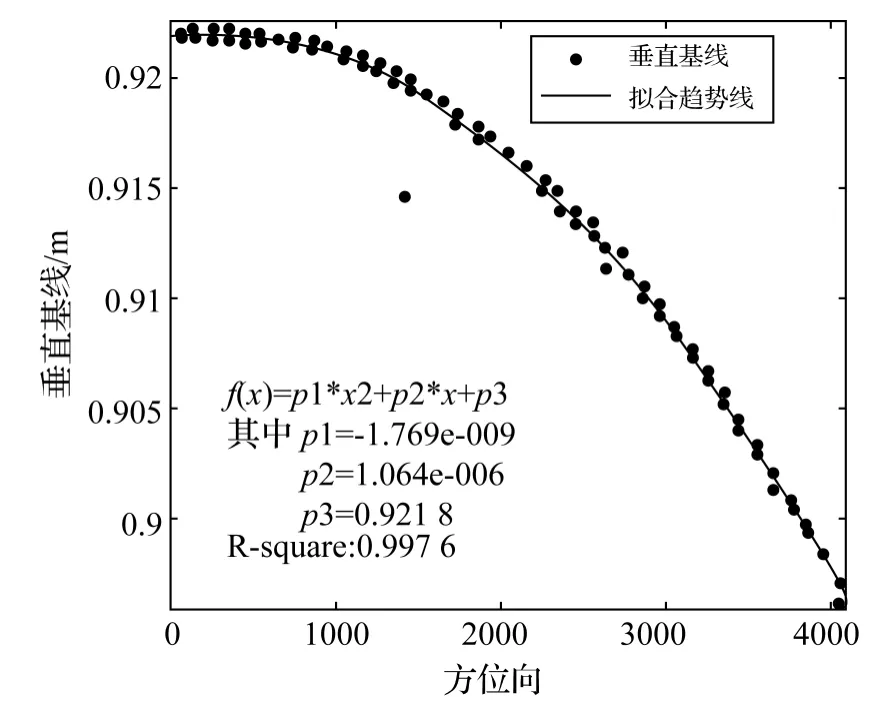
图5 垂直基线随方位向变化趋势拟合Fig.5 Fitting of perpendicular baseline and pixels along azimuth

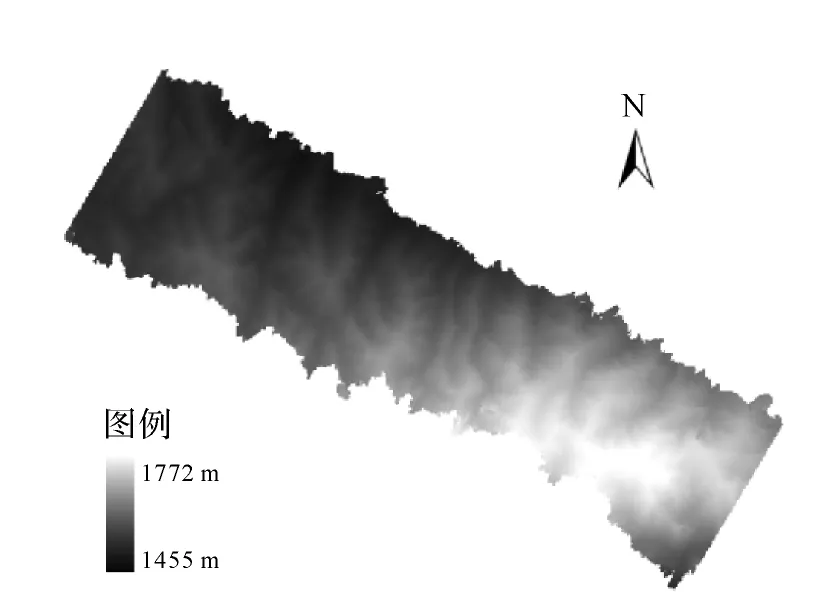
图6 InSAR生成的DEMFig.6 DEM generated from InSAR

表2 干涉定标过程和结果Tab.2 Calibration processes and results

3.4 定标精度检验

在SAR图像模拟阶段，模拟图像和真实图像的平面误差为0.732像元，研究区平均坡度为27.78°，由平面误差带来的高程误差平均值为0.38m，因此这里不再考虑图像模拟中平面位置偏移带来的高程误差。由于参考DEM的空间分辨率为5m，InSAR生成的DEM分辨率为1m，为了减少细节信息的损失，将5m的参考DEM插值至1m后进行做差。定标精度检验是整幅图像所有点都做差，用于高程检验的点达400万个，其中用于定标的有313个，去掉定标点后对整体高程偏差的分布没有影响，因此这里全部点都参与定标精度检验，定标前后的高程偏差结果如图7。

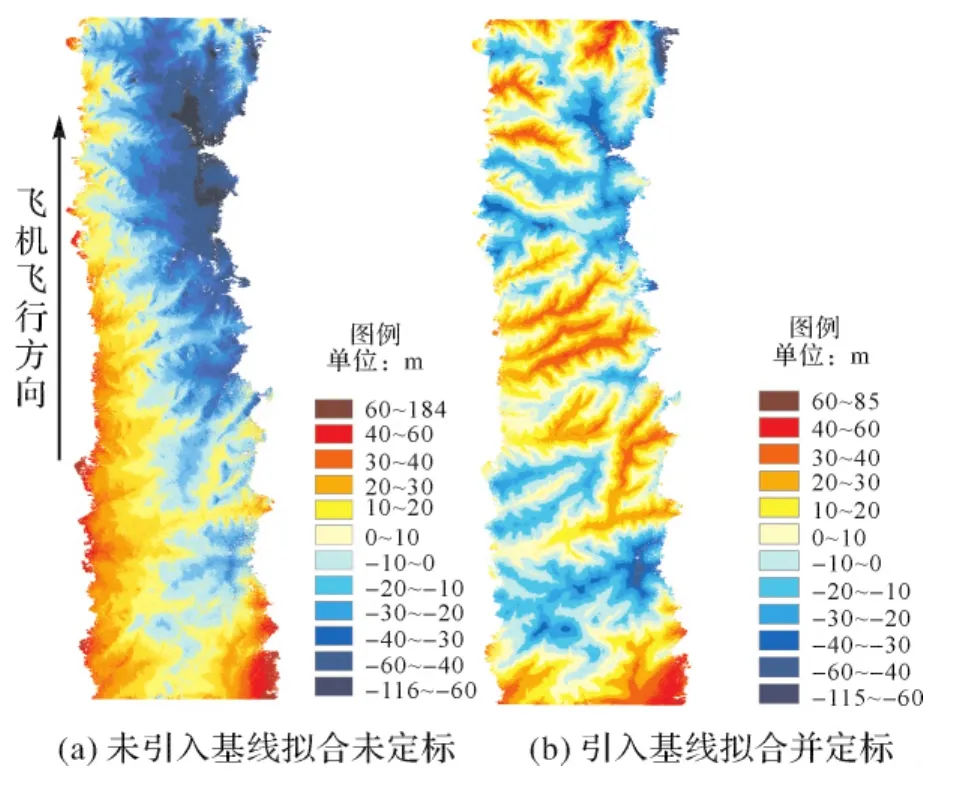
图7 InSAR DEM与参考DEM高程偏差分布图Fig.7 Difference between InSAR DEM and reference DEM

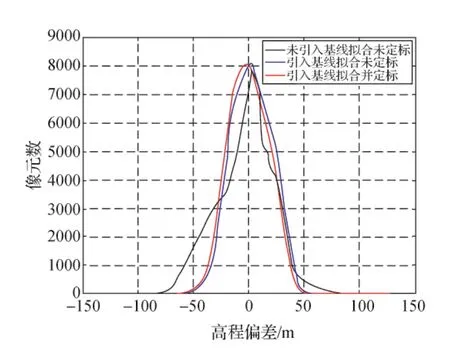
图8 InSAR生成DEM与参考DEM高程偏差分布直方图Fig.8 Histogram of height difference

通过和参考DEM反映出的地形进行对比，高程偏差和地形的对应关系为：高程偏差高值对应于沟谷等低地（图7（b）中红色系图例对应的在参考DEM上为低地），低值对应于山脊等高地（图7（b）中蓝色系图例对应在参考DEM上为高地），即在沟谷地形中由InSAR系统得到的高程高于参考DEM中对应的高程，而在山脊高地区，InSAR得到的高程低于参考DEM对应的高程。将定标过程中的高程偏差进行直方图统计（图8）竖线表示众数所在的位置。统计各直方图众数对应的高程差值，结果如表3。

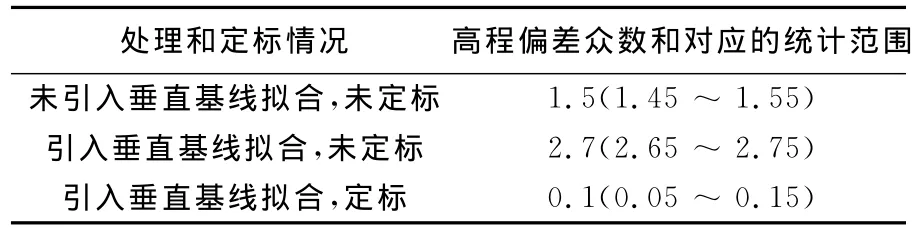
表3 不同处理和定标情况下直方图分布众数对应的高程偏差统计Tab.3 Statistics of height error in difference calibration process m

经过垂直基线拟合和定标得到的高程偏差众数为0.1，定标结果有效收敛。对该结果作分布频率统计，试验的高程精度要求为2～4m，以此为一项统计范围；参考DEM高程中误差为5m，考虑到参考DEM本身的偏差，以±5m和±9m也作为统计范围，结果见表4。此外，定标后的结果近似为正态分布，在正态分布曲线下，横轴区间（μ－σ，μ＋σ）内的面积为68.3%，表征主体分布范围；区间（μ－1.96σ，μ＋1.96σ）内的面积为95%；区间（μ－2.58σ，μ＋2.58σ）内的面积为99%，表征总体分布范围。以上述分布面积统计相应高程偏差的范围，结果如表4。

表4 高程偏差直方图分布频率和分布范围统计Tab.4 Statistics of the height difference histogram

经过上述统计，采用无人工靶标的干涉定标得到的DEM和参考DEM存在误差的原因主要有：① 参考DEM本身的误差。按照测绘行业标准（CH／T 9009.2－2010），DEM 精度分为三级，三级DEM的精度为：1∶1万DEM山地高程中误差在5m内、高山地10m内，本文由参考DEM确定GCP坐标，又以其作基准进行做差，这两步中DEM本身的误差都会对结果造成一定偏差；② 图像模拟的误差：利用31个控制点检验模拟图像和真实图像的偏差，均方误差平均值为0.732像元，该研究区最大坡度73.06°，平均坡度27.78°，坡度值主要分布在11°～45°，由平面误差可能带来的高程误差平均值为0.38m，最大值为2.40m，对应主要坡度分布范围的高程误差为0.14～0.73m；③ 以往研究通过地面检验点来进行结果检验，点的分布范围和数量有限。本试验采用整体DEM做差，而试验区位于山区，地形本身的复杂性也导致这种验证存在一定的偏差。此外，通过和地形的对比，高程偏差的高低值区和地形的对应关系显著，由于参考DEM的获取通常是通过等高线和测点差值得到，且采样间隔远大于InSAR的分辨率，故在高地和沟谷地进行差值会对得到的参考DEM高程造成一定误差。

4 结 论

本文提出一种无人工靶标的干涉定标方法并利用无人机InSAR数据进行了试验验证，结论如下：

（1）利用本文的定标方法可获得一系列GCP及其坐标，得到的点数量多且分布均匀。在没有人工靶标的情况下，利用本方法不仅能提高生成DEM的精度，减少了野外布设的人力、物力，在一些紧急情况下可以快速完成干涉参数定标并生成地形产品。以往研究通过数量有限的检验点来判断定标精度，而本文采用整个试验区范围内的DEM数据进行做差和统计，并分析了误差与地形的关系。

（2）在敏感度方程解算方面，以往的解算方法不考虑系统初始值对迭代的影响，而一些不精确的初始值会使迭代发散，从本研究的实际情况来看，仅靠敏感度模型对初值不精确的系统定标时，定标效果并不理想，因此本文利用牛顿下山法的对敏感度方程解算进行改进使结果有效收敛。

（3）由常规干涉处理得到的高程偏差有随方位向变化的趋势，这与无人机飞行姿态的不稳定有关，本文将基线长度的改正耦合在干涉处理和定标中，能很好地消除飞行过程中垂直基线的变化趋势。

在干涉定标中，如何得到位置误差矩阵是干涉定标的关键问题之一，在有人工靶标的干涉定标中，利用在SAR图像上能够识别的人工靶标建立InSAR得到的坐标和真实坐标的联系，而在无人工靶标的干涉定标中是利用模拟SAR图像建立InSAR得到的坐标和参考DEM坐标（作为真实坐标）的联系。如果在试验区布设少量人工靶标，理论上可使定标结果更加精确。在没有人工靶标的情况下，利用本文的方法可以去掉InSAR生成DEM中的趋势性误差，但结果也表明定标后得到的DEM与参考DEM仍有一定差异，一方面是由于参考DEM本身的误差，另一方面，在引入基线拟合的干涉处理过程中的基线估计可能仍不准确，因此如何在干涉处理中更好地修正基线的误差也是定标处理的关键问题之一，故进一步的工作将着重于干涉处理与干涉定标的耦合问题。

［1］ ZHANG Wei.Airborne Dual－antenna InSAR′s Interferometric Calibration Method Research［D］.Beijing：Institute of Electronics Chinese Academy of Sciences，2009.（张薇.机载双天线干涉SAR定标方法研究［D］.北京：中国科学院电子学研究所，2009.）

［2］ CHAPIN E，HENSLEY S，MICHEL T R.Calibration of an Across Track Interferometric P－band SAR ［C］∥Proceedings of IGARSS 2001.Sydney：IGARSS，2001：502－504.

［3］ MALLORQUI J J，BARA M，BROQUETAS A.Calibration Requirements for Airborne SAR Interferometry［C］∥Proceedings of SPIE－Int Soc Optical Engineering.Bellingham：［s.n.］，2000：267－278.

［4］ MALLORQUI J J，BARA M，BROQUETAS A.Sensitivity Equations and Calibration Requirements on Airborne Interferometry［C］∥Proceedings of IGARSS 2000.Honolulu：［s.n.］，2000：2739－2741.

［5］ WANG Yanping.Studies on Calibration Model and Algorithm for Airborne Interferometric SAR［D］.Beijing：Institute of Electronics Chinese Academy of Sciences，2003.（王彦平.机载干涉SAR定标模型与算法研究［D］.北京：中国科学院电子学研究所，2003.）

［6］ WANG Yanping，PENG Hailiang.3DReconstruction of Targets in Interferometric SAR［J］.Journal of Electronics＆Information Technology，2003，25（9）：1187－1193.（王彦平，彭海良.干涉合成孔径雷达目标的三维重建［J］.电子与信息学报，2003，25（9）：1187－1193.）

［7］ ZHANG Wei，XIANG Maosheng，WU Yirong.Realization of Outside Calibration Method Based on the Sensitivity Equation for Dual－antenna Airborne Interferometric SAR［J］.Remote Sensing Technology and Application，2009，24（1）：82－87.（张薇，向茂生，吴一戎.基于三维重建模型的机载双天线干涉SAR外定标方法及实现［J］.遥感技术与应用，2009，24（1）：82－87.）

［8］ ZHANG Wei，XIANG Maosheng，WU Yirong.Using Control Points′3DInformation to Calibrate the Interferometric Parameters of Dual－antenna Airborne InSAR Systems［J］.Acta Geodaetica et Cartographica Sinica，2010，39（4）：370－377.（张薇，向茂生，吴一戎.利用控制点三维信息标定机载双天线干涉SAR参数［J］.测绘学报，2010，39（4）：370－377.）

［9］ MALLORQUI J J，RPSADO I，BARA M.Interferometric Calibration for DEM Enhancing and System Characterization in Single Pass SAR Interferometry［C］∥Proceedings of IGARSS 2001.Sydney：IGARSS，2001：404－406.

［10］ WANG Yanping，PENG Hailiang，YUN Risheng.Locating Calibrators in Airborne InSAR Calibration［J］.Journal of Electronics ＆Information Technology，2005，26（1）：89－94.（王彦平，彭海良，云日升.机载干涉合成孔径雷达定标中的定标器布放［J］.电子与信息学报，2004，26（1）：89－94.）

［11］ TEILLET P M，SLATER P N，DING Y，et al.Three Methods for the Absolute Calibration of the NOAA AVHRR Sensors in－flight［J］.Remote Sensing of Environment，1990，31（2）：105－120.

［12］ YANG Huaining，GUO Huadong，HAN Chunming.Imitation Experiment on the Parameter Requirements of the Sensitivity Equation－based Calibration for Airborne InSAR［J］.Chinese High Technology Letters，2010，20（10）：1049－1054.（杨怀宁，郭华东，韩春明.机载InSAR敏感度方程定标限制条件的仿真试验［J］.高技术通讯，2010，20（10）：1049－1054.）

［13］ LI Pin，ZHANG Dongchen，WANG Dongjin，et al.Research on the Differential Interferometric Calibration for InSAR Systems［J］.Journal of University of Science and Technology of China，2009，39（5）：460－465.（李品，张冬晨，王东进，等.InSAR系统差分干涉定标的研究［J］.中国科学技术大学学报，2009，39（5）：460－465.）

［14］ WANG Jinhua，LI Pin，CHEN Weidong.An Interferometric Calibration Method Based on Genetic Algorithm for InSAR System［J］.Journal of University of Science and Technology of China，2010，40（2）：133－139.（汪金华，李品，陈卫东.基于遗传算法的InSAR系统干涉定标方法［J］.中国科学技术大学学报，2010，40（2）：133－139.）

［15］ JIN Guowang，ZHANG Wei，XIANG Maosheng，et al.A New Calibration Algorithm of Interferometric Parameters for Dual－antenna Airborne InSAR［J］.Acta Geodaetica et Cartographica Sinica，2010，39（1）：76－81.（靳国旺，张薇，向茂生，等.一种机载双天线InSAR干涉参数定标新方法［J］.测绘学报，2010，39（1）：76－81.）

［16］ MADSEN S N，ZEBKER H A，MARTIN J.Topographic Mapping Using Radar Interferometry：Processing Techniques［J］.IEEE Transactions on Geoscience and Remote Sensing，1993，31（1）：246－256.

［17］ MAO Yongfei，XIANG Maosheng.Joint Calibration of Airborne Interferometric SAR Data Using Weighted Optimization Method［J］.Journal of Electronics ＆Information Technology，2011，33（12）：2819－2824.（毛永飞，向茂生.基于加权最优化模型的机载InSAR联合定 标 算 法 ［J］.电 子 与 信 息 学 报，2011，33（12）：2819－2824.）

［18］ LI Qingyang，WANG Nengchao，YI Dayi.Numerical Analysis［M］.Beijing：Tsinghua University Press，1983：231－233.（李庆扬，王能超，易大义.数值分析［M］.北京：清华大学出版社，1983：231－233）

［19］ YUN Y，ZENG Q M，JIAO J，et al.Calibration of Airborne Interferometric SAR Data by External DEM without Artificial Calibrators［C］∥Proceedings of IGARSS 2012.Munich：［s.n.］，2012：4501－4504.

［20］ WANG Qing，ZENG Qiming，JIAO Jian，et al.Highresolution Airborne SAR Image Simulation Based on RD Model and DEM Data［J］.Science of Surveying and Mapping，2013（4）：134－137.（王庆，曾琪明，焦健，等.基于RD模型和DEM数据的高分辨率机载SAR图像模拟［J］.测绘科学，2013（4）：134－137.）