电磁波电场与磁场相位的疑惑与通俗演义

费 宏

（常州市第一中学，江苏 常州 213003）

1 中学课本对电磁场描述

1.1 根据麦克斯韦理论：变化电场能产生磁场，变化的磁场能产生电场，变化的电磁场由近及远的传播即电磁波.

1.2LC电磁振荡可以得到周期性变化的电场与磁场.如果电路开放就能形成电磁波.

1.3 电磁波是横波，电场和磁场相互垂直，并且电场与磁场的振荡是同相的.

2 困惑与问题

2.1 困惑与问题

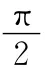
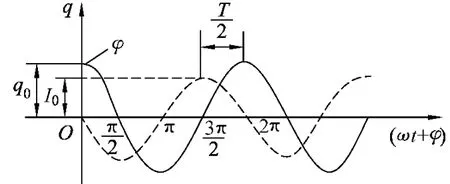
图1

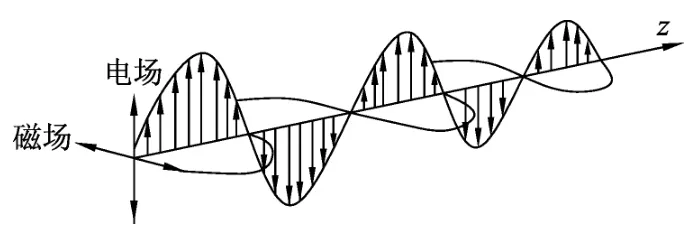
图2

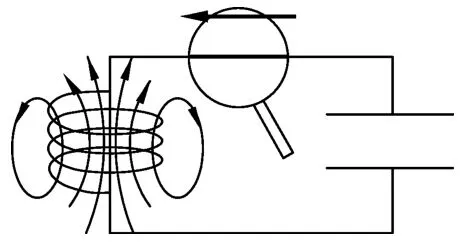
图3

2.2 无阻尼LC电磁振荡

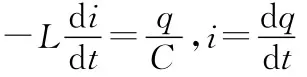
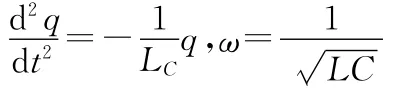
解微分方程

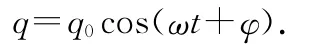
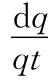
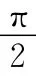
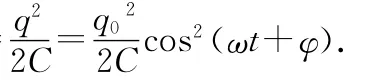
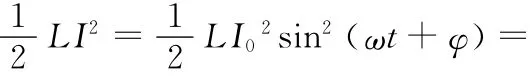
电场能量与磁场能量互相转化，但总能量保持不变.无阻尼自由电磁振荡是理想化的模型，它要求：

①LC回路电阻为0，因此回路不会因产生的焦耳热而损失电磁能；

②LC回路不存在电动势，没有其他的能量转化为电磁能；

③ 电磁能只能在LC内相互转换，还不能以电磁波的形式辐射出去.

2.3 大学电动力学对现行课本所给电磁波图的论证

脱离了场源的无界空间中，没有自由电荷和传导电流，即ρ＝0，j＝0，

麦克斯韦方程组为

如果电磁波在真空中传播，则有D＝ε0E，B＝μ0H，于是麦克斯韦方程组变为

由（5）、（6）式消去B就可得到关系E的偏微分方程，而后两端取旋度，交换时间与空间微商的次序，然后代入（1）式，有

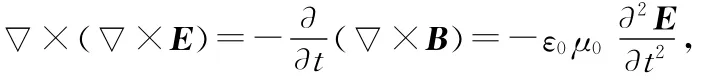
利用矢量运算关系▽×（▽×E）＝▽（▽·E）－▽2E及（7）式，整理得

同样的方法得

上式形成的方程称为波动方程.

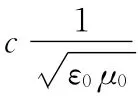
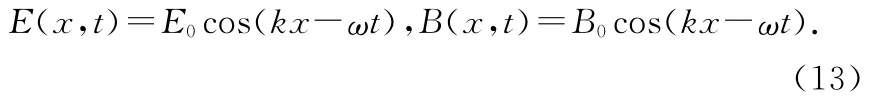
（13）式给出了在x处t时刻的场矢量，由于是平面波，所有距yOz面为x的平面上，在t时刻的场矢量具有相同的值，因此观察点的位置矢为r，取矢量k，称为波矢量，它的方向为波的传播方向大小为波数k，则kx＝k·r，则解可改写成

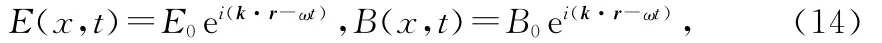
（14）式表示平面波，传播方向已不限于沿x轴，k可为任意方向，而k·r＝kxx＋kyy＋Kzz，由于E，B需分别满足▽·E＝0，▽·B＝0，将（14）代入▽·E＝▽ei（kr－ωt）·E0＝ik·E0ei（k·r－ωt）＝ik·E，即得k·E＝0，同理

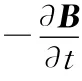
3 通俗演义

大学电动力学是根据麦斯韦方程组对电磁场规律的严格论证，结论正确无误，所以中学课本所给的电磁波传播图是正确的.但是以上论证让中学师生很难看懂.我们希望：尽可能避免高深理论，最好能在中学师生的最新发展区通俗易懂地讲清这个问题.

3.1 中学师生前概念分析

（1）根据麦克斯韦原理，变化的磁场能感应电场，变化的电场等效电流，而电流周围有磁场.（2）电场与磁场是做周期性变化的，电场与磁场相互垂直.（3）电磁波是电磁振荡在空间的传播.

3.2 处理问题的要点分析

（1）LC振荡电路能产生振荡的电磁场，振荡的电磁场是产生电磁波的必要条件但不充分，也即封闭LC振荡电路是不能形成电磁波的.（2）开放的LC电路，只能等效一个振荡电偶极子，由于传播距离R远于偶极距L，空间传播电磁波应该是一个球面波，或直接看成平面波.单纯地认为电磁振荡只与时间有关是错误的，电磁波应该是时间和位移的函数，必须遵守电磁场理论.

3.3 难点化解

即变化磁场产生旋转电场.

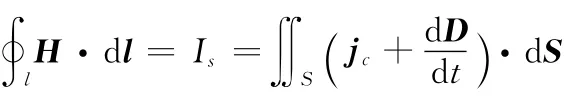
其中D＝ε0E，B＝μ0H得

即变化电场产生旋转磁场.

设平简谐波沿x方向传播，根据横波特性，设电场矢量E在xoy平面内振荡，磁场矢量B在xoz平面内振荡.根据以上分析平面电磁波方程平面简谐的表达式，用Ey和Bx表示为

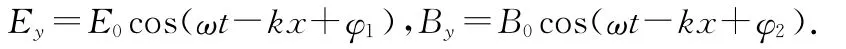
其中φ1、φ2分别是在x＝0处（原点）电振荡与磁振荡的初位相.要说明E、B是同相位，就凭以上2式还不能够说明，原因是波动程是E与B彼此独立的波动方程，要证明E与B同相，必须根据E和B的相互联系的规律，即

（16）分量表示式为

（17）分量表示式为

对以上2式求导

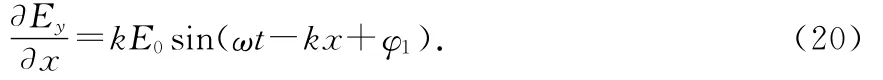
将（20）、（21）代入（18）式得

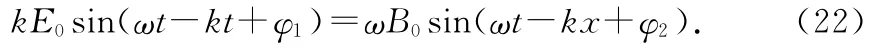
（22）式的两端都是时间t和空间坐标x的正弦函数，要该式成立必须

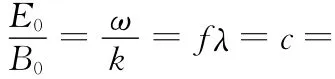
结束语：电磁波是横波，电磁振荡是一个谐函数，对应的电磁波也该是一个谐函数，电场、磁场和传播方向矢量必须满足右手螺旋法则，磁场对时间的变化率等同于电场对空间的变化率.

说得再明确些，平面电磁波的特性为

（1）电磁波为横波，E和B都与传播方向垂直；

（2）E和B互相垂直，E×B沿波矢k方向；

（3）E和B同相，振幅比为C.（见郭硕鸿电动力学第二版高等教育出版社142页）

1 阚仲元.电动力学教程［M］.北京：人民教育出版，1979：105－113.

2 唐果南.教师教学用书（选修3-4）［M］.北京：人民教育出版社，2010：97－98.