利用数学软件MathCAD模拟无阻尼条件下平面振子的真实运动
2014-07-25邢云开
黄 晶 汪 飞 邢云开
(1.嵊州中学,浙江 嵊州 312400;2.海门中学,江苏 海门 226100;3.嵊州市长乐中学,浙江,嵊州 312400)
1 问题的提出
不少高中物理竞赛辅导资料[1,2]中将下列平面振子的题目作为分方向简谐运动合成的典型例题,我们发现其解答分解过程存在问题,导致试题最终解答也是错误的,值得我们深入研究,原题如下.
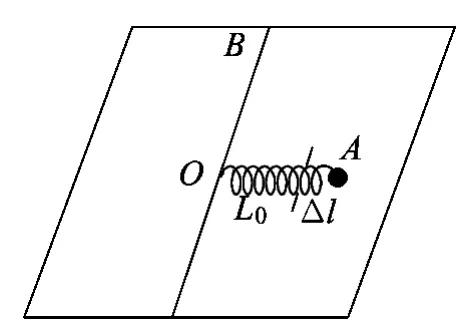
图1
题目.如图1所示,置于光滑水平面上的轻质弹簧原长为L0,劲度系数为k,一端固定在O点,另一端系一质量为m的小球.现沿某方向将弹簧拉长Δl至A点,然后以垂直于OA方向并沿水平面将小球以速度v0射出.求:(1)小球绕O点转过90°至B点的时间;(2)OB的长度.
参考解答:如图2所示,以O点为坐标原点,OA方向为x轴,OB方向为y轴建立直角坐标系xOy,当小球运动至一般位置C时,OC与x轴的夹角为θ,此时弹簧对小球的作用力F=k(OCL0),沿x、y方向的分量分别为
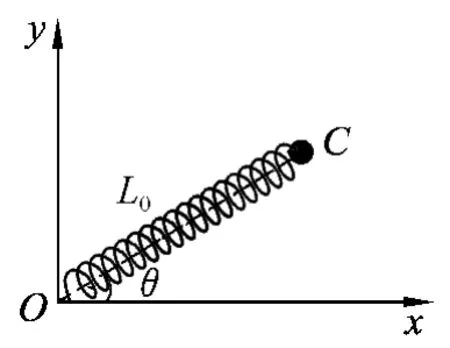
图2
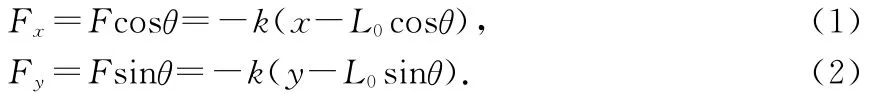
其中x-L0cosθ、y-L0sinθ分别为沿x轴和y轴方向的弹簧的伸长量.
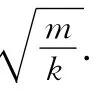
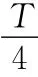
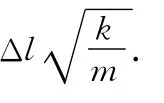
根据机械能守恒定律,设沿y方向弹簧伸长Δy,对A点和B点有
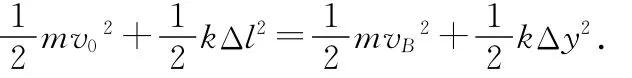
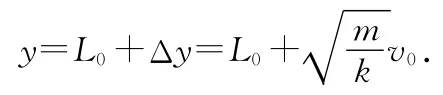
2 演绎推理质疑
从解答结果看,A运动到B的时间与到达B点小球的速度均与初速度v0无关.我们可以考虑简单的特殊情况加以验证.
若v0趋向于0,则小球的运动变为一维的弹簧振子,小球是无法到达y轴上y=L0处,这与参考答案矛盾.
若小球的速度大小合适,使得弹簧的弹力等于小球绕O点做匀速圆周运动的向心力,即
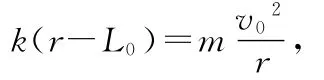
其中r为做匀速圆周运动的半径.解得
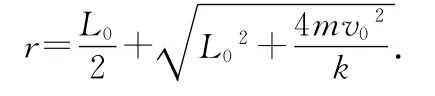
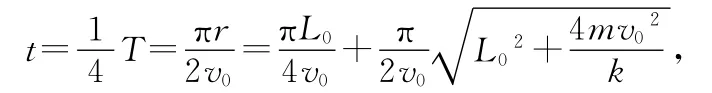
到B点的速度为v0,OB的长度为r,显然这也与参考答案矛盾.
质疑:小球在x、y方向果真做周期相同的简谐振动吗?
3 数学方程表征
根据前面的坐标系约定和受力分析以及几何关系有
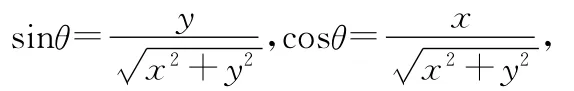
可得平面振子在x、y方向上的动力学微分方程为
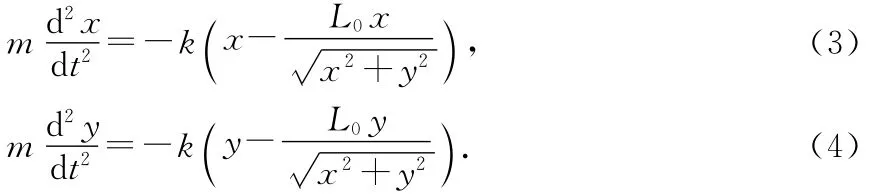
4 软件数值计算
要获得小球真实的运动情况需解非线性微分方程组,十分困难.下面用数学软件MathCAD进行数值计算.
首先设置振子的参数和初始条件如下:弹簧原长L0=0.4m,劲度系数k=50N/m,初始伸长量ΔL=0.1m,小球质量m=0.5kg.
4.1 特殊情况
当初速度v0=0m/s时绘制小球振动轨迹如图3所示,小球的运动变为一维的弹簧振子;当初速度为v0=m/s时,小球做匀速圆周运动,轨迹如图4所示.
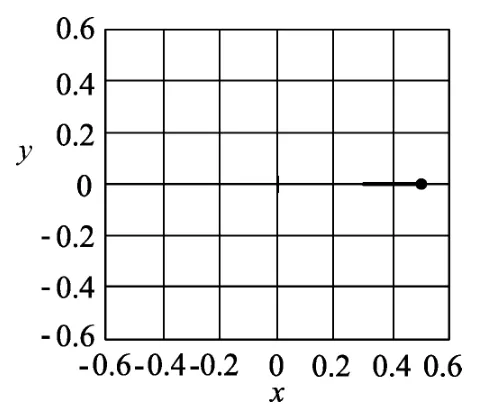
图3
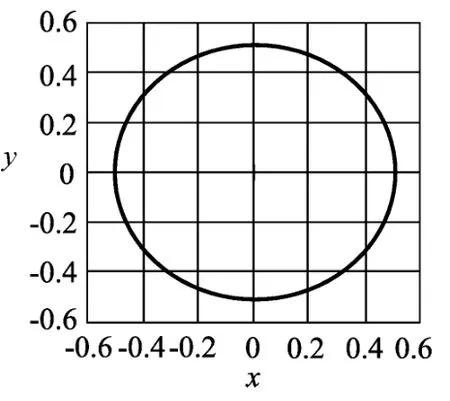
图4
4.2 一般情况
当初速度v0=10m/s时,绘制小球转过90°到B点的轨迹图如图5所示.小球运动到B点时,B点的竖直位移不是整个过程的最大值,速度不是水平方向,由数学软件数值计算可得A到B的时间为t=0.230s,B点的速率为vB=5.049m/s,OB的距离为y=1.246m;图6为小球转动一周的轨迹图,运动一周后小球并没有回到A点且速度方向不是竖直向上的.
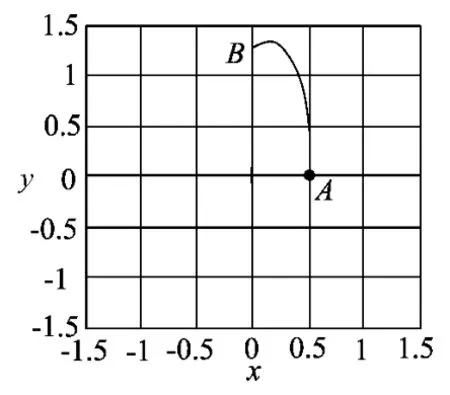
图5
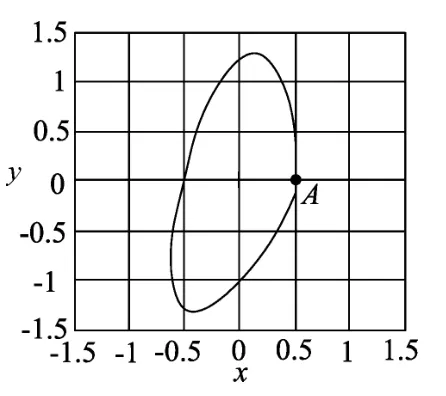
图6
绘制小球前10次回到x正半轴的轨迹图,如图7所示,小球的运动轨迹呈规则的花瓣状;小球前100次回到x正半轴的轨迹如图8所示,小球的运动被限止在一个内切圆与一个外切圆之间,随着时间的变长,瓣状轨迹越来越密集,说明运动轨迹不存在重合现象,反映平面振子复杂的周期性运动.
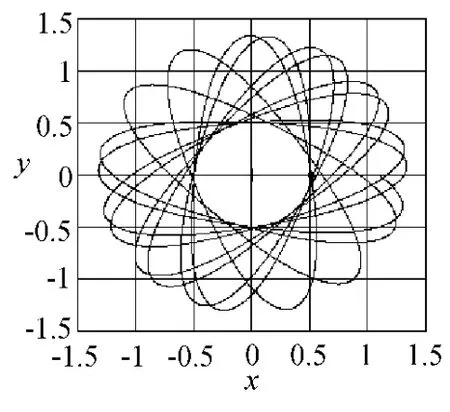
图7
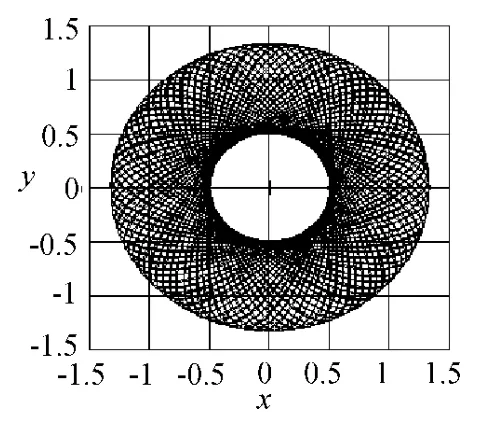
图8
4.3 分方向简谐运动的验证
绘制小球前10次回到x正半轴时间内振子的x-t图、y-t图、vx-t图和vy-t图如图9~12所示,由图可直观地看到振子在x、y方向的分运动不是简谐运动,参考解答中将小球的运动分解为x方向与y方向的简谐运动的方法是错误的.
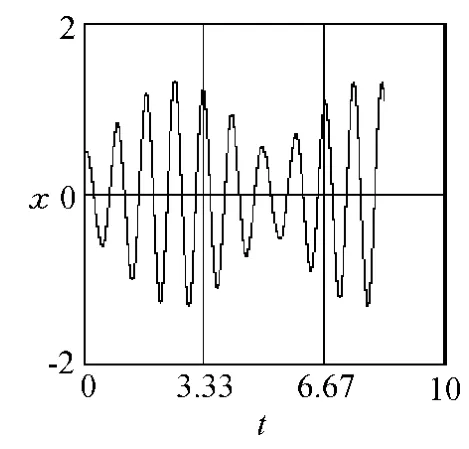
图9
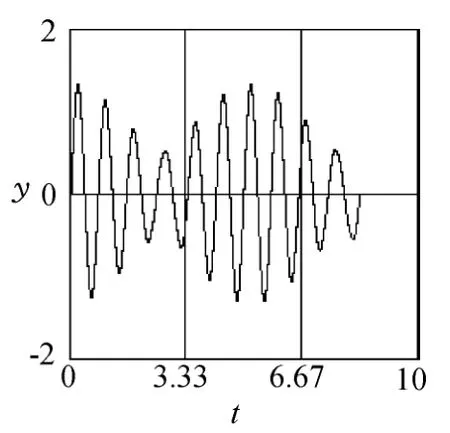
图10
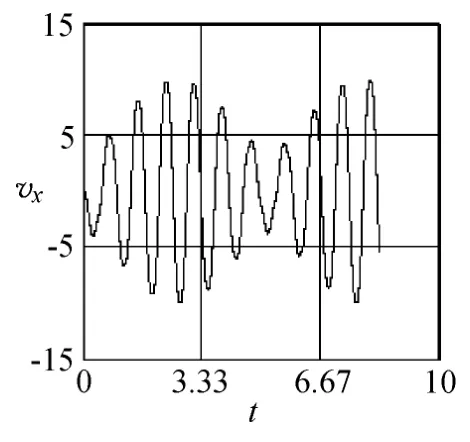
图11
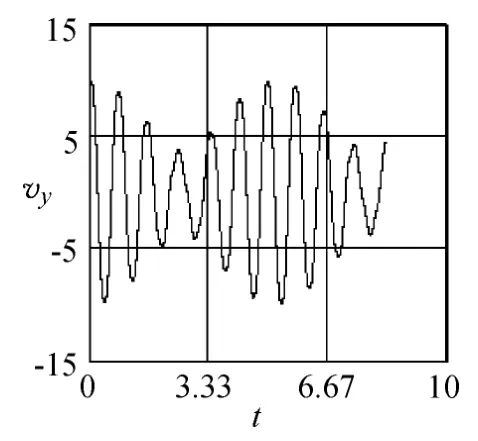
图12
5 问题的解决
那么竞赛资料的参考解答的问题在哪里?观察(1)、(2)两式可得平面振子在水平方向与竖直方向的原长是随θ变化的,由此得出的回复力与相对平衡位置成正比的观点是错误的,参考解答在此错误的前提下推得振子的运动分解为x、y两个方向独立的简谐运动是错误的,导致结果也是错的;事实上由(3)、(4)两式更容易看出,每个方向的微分方程中都包含了另一方向上的位移分量,反映出这两个方向的分运动之间是彼此关联,并不是独立的.将复杂运动正交分解为两个便于研究的直线运动是简化复杂运动的重要研究方法,但前提必须要使两个方向上的分运动是彼此独立的.
附录:MathCAD程序
设置初始条件:
x初始位置Z0∶=5 x方向初始速度 Z2∶=0
y初始位置Z1∶=0 y方向初始速度 Z3∶=10
设置运动的时间T∶=8.269
建立D函数:
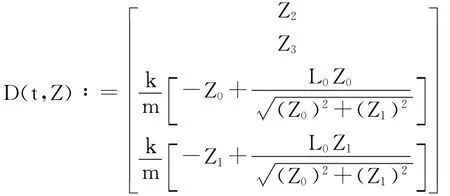
求解微分方程组:
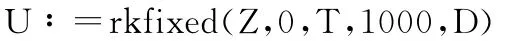
得到各量的数值结果:
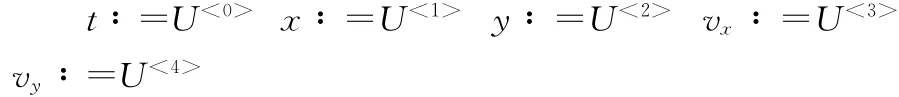
1 范小辉.新编高中物理奥赛实用题典[M].南京:南京师范大学出版社,2008:333.
2 舒幼生,钟小平.高中物理竞赛培优教程[M].杭州:浙江大学出版社,2008:180.
3 闻邦椿,刘树英,陈照波,李鹤.机械振动理论及应用[M].北京:高等教育出版社,2009:148.
4 宋征,林勇等.MathCAD7.0入门及其工程应用[M].北京:人民邮电出版社,1999.
