从一个实例分析电磁场的能量

黄 辉

（宁波市惠贞书院，浙江 宁波 315016）

赫兹通过实验证实了电磁波的存在，这意味着，电磁场不仅是一种描述方式，而且是一种真正的物理实在.天线辐射电磁波，电磁能量随着电磁波的传播不断地从天线传向远方.在空间各点上，用接收器都可以接收到电磁波的能量.不同于一般的实物，电磁场的概念比较抽象.

本文研究一导体棒在处于匀强磁场中的平行板电容器内的运动这一非常简单常见的物理模型.通过定性分析和定量计算，论证电磁场具有能量，它们不仅可以与机械能相互转换，而且在转换过程中满足能量守恒定律.这一模型让初学者对电磁场的能量有一个简单、直观的感受，从而能更好地理解电磁场的能量.

1 匀强磁场中的平行板电容器

两导体板相距为L的平行板电容器，电容为C.如图1所示，处在匀强磁场中.磁场的方向与导体板平行，大小为B.将平行板电容器充电，使两极板所带的电荷量为Q0.然后将一质量为m，电阻为R，长度为L的导体棒垂直放在电容器的两板之间.

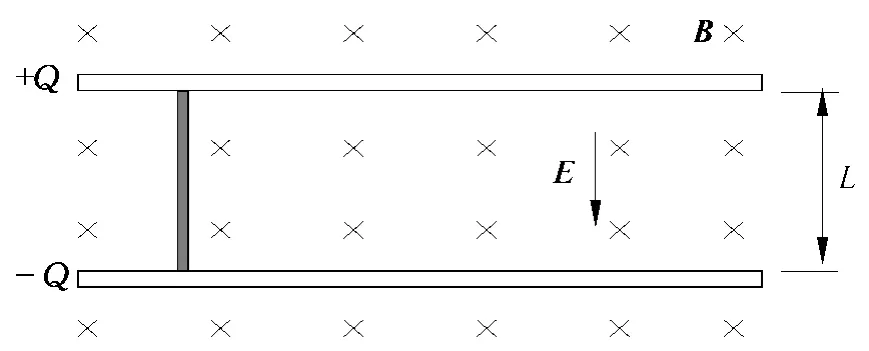
图1

导体棒上的电流导致电容器两极板上的电荷量减少，使得板间电场减小；另外，根据楞次定律，导体棒运动时产生感应电动势，电动势方向也与板间电场相反.所以，导体棒上的电流会逐渐变小，安培力和加速度也随之减小.然而在加速度减小为0之前，导体棒的速度还在变大，感应电动势继续变大，电流继续变小，直到电容器极板上的剩余电荷量产生的电压与感应电动势相等，彼此平衡.此时，导体棒上的电流为0，电容器极板上的电荷量为Qmin，不再改变，板间电场也不再变化.导体棒的速度达到最大，并以此速度vmax做匀速运动，即

由导体棒的运动方程

可知，速度的变化率直接正比于电荷量的变化率，因此

联立式（1）和式（3）可求出

和

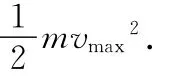
2 电磁场的能量

导体棒的动能是哪里来的？当我们把导体棒作为研究对象时，我们会说，是磁场作用于导体棒的安培力做功改变了导体棒的动能.但当我们把导体棒和电容器以及磁场看作一个整体系统时，我们发现，并没有任何外力作用于这个系统，而导体棒却获得了动能.唯一的解释就是，在系统内一定有另一个对象，它失去了相等数量的能量.失去能量的就只能是电磁场.

研究能量的变化，由（4）式得，导体棒最后获得的动能是

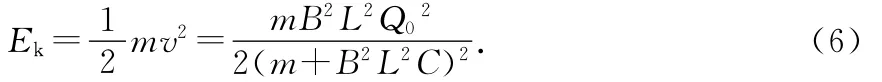
另外，由于导体棒在加速运动过程中一直流有电流，从而不断产生焦耳热.回路中的电流遵从欧姆定律

两边取微分得

将（2）式代入上式得

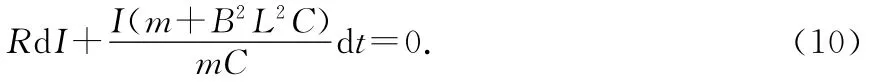
分离变量得

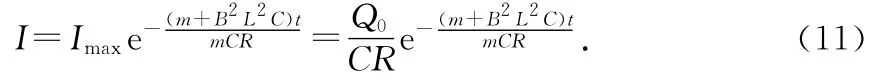
积分得整个过程中产生的焦耳热

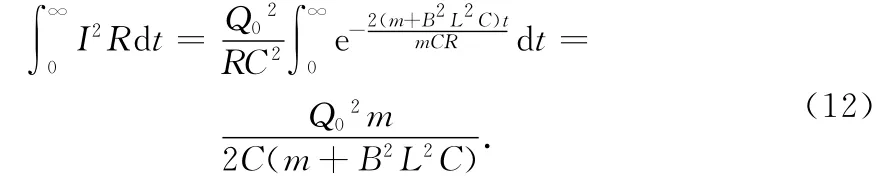
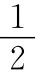
将（6）式和（12）式相加，就是（14）式.即导体棒获得的动能与整个过程的焦耳热之和等于电磁场能量的减少.

3 结论

通过分析处于匀强电磁场中的平行板电容器中导体棒的运动，从一个侧面论证了电磁场的确具有能量，并且可以与其他形式的能量相互转换，在转换过程中遵循能量守恒定律.这一简单的模型使得原本抽象的概念变得具体化，有利于初学者对电磁场的这一重要属性的理解.

1 郭硕鸿.电动力学（第2版）［M］.北京：高等教育出版社，1997.

2 程守诛，江之永.普通物理学2（第2版）［M］.北京：高等教育出版社，1998.