巧用曲率半径求解拱点速度

金 彪

（浙江省春晖中学，浙江 绍兴 312353）

开普勒定律告诉我们，每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中.我们先求椭圆拱点的曲率半径.设平面直角坐标系中，有一动点的位置坐标为

可以证明该动点的运动轨迹为椭圆，求导可以得到该点的速度为

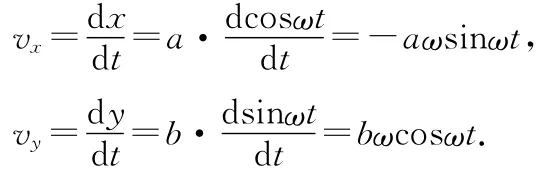
再一次求导，可得到该点的加速度为

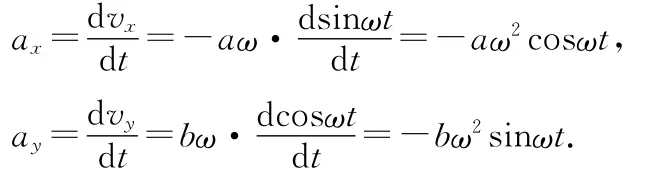
在0时刻，动点位于拱点（a，0），此时速度为

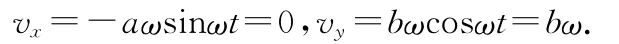
加速度为

由此可求得该点上椭圆的曲率半径为

当某一天体绕中心天体做椭圆运动时，近心点离引力中心的距离为R1＝a－c（c为椭圆半焦距，且有c2＝a2－b2），万有引力产生的加速度为

则由向心力公式可得此时绕行天体的瞬时速度为

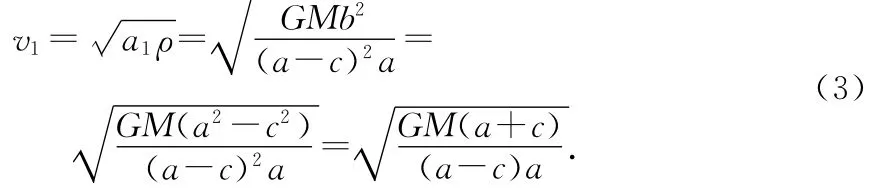
当绕行天体在远心点时，绕行天体离引力中心的距离为R2＝a＋c，同理可得绕行天体在远心点的速率满足

上面（3）、（4）两式为绕行天体在近、远2个拱点的瞬时速度与中心天体质量、半长轴、半焦距的关系式.下面我们就用此解几个竞赛题.

例1.（第23届预赛第9题）如图1，从赤道上的C点发射洲际导弹，使之精确地击中北极点N，要求发射所用的能量最少.假定地球是一质量均匀分布的半径为R的球体，R＝6400km.已知质量为m的物体在地球引力作用下做椭圆运动时，其能量E与椭圆半长轴a的关系为

式中M为地球质量，G为引力常量.

（1）假定地球没有自转，求最小发射速度的大小和方向（用速度方向与从地心O到发射点C的连线之间的夹角表示）.

（2）若考虑地球的自转，则最小发射速度的大小为多少？

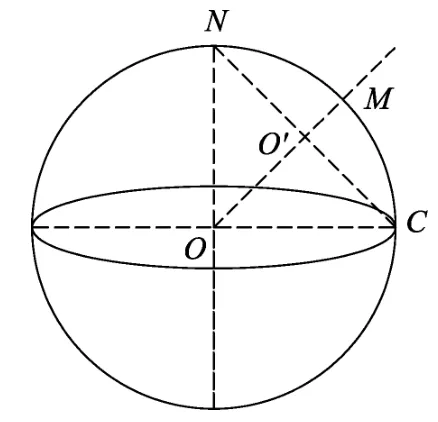
图1

在这里不讨论（1）、（2）两小题的求解，直接看第3小题，我们可以这样解.

解析：根据上面（3）式，可得洲际导弹在近地点的动能大小为

同时可以求得势能大小为

则

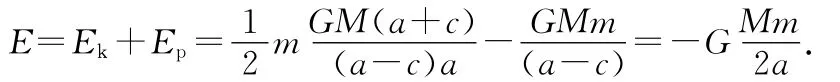
例2.（第17届复赛第4题）宇宙飞行器和小行星都绕太阳在同一平面内做圆周运动，飞行器的质量比小行星的质量小得很多，飞行器的速率为v0，小行星的轨道半径为飞行器轨道半径的6倍.有人企图借助飞行器与小行星的碰撞使飞行器飞出太阳系，于是他便设计了如下方案：

Ⅰ.当飞行器在其圆周轨道的适当位置时，突然点燃飞行器上的喷气发动机，经过极短时间后立即关闭发动机，以使飞行器获得所需的速度，沿圆周轨道的切线方向离开圆轨道；

Ⅱ.飞行器到达小行星的轨道时正好位于小行星的前缘，速度的方向和小行星在该处速度的方向相同，正好可被小行星碰撞；

Ⅲ.小行星与飞行器的碰撞是弹性正碰，不计燃烧的燃料质量.

（1）试通过计算证明按上述方案能使飞行器飞出太阳系；

解析：（1）根据题意，设太阳质量为M0，飞行器加速前速率为

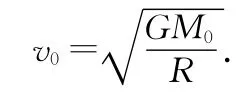
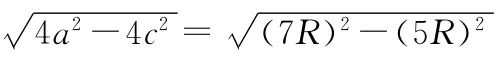
由（3）、（4）两式可以求得飞行器在近日点与远日点的速度分别为

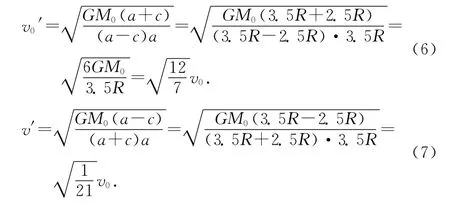
同时，可以求得小行星的速率为

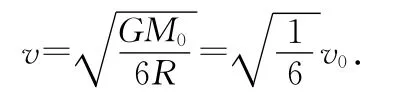
当飞行器与小行星碰撞时，以太阳为参考系，小行星与飞行器整体的机械能与角动量均守恒，设碰后飞行器与小行星的速度分别为v1、v2，则有

将（8）式的v2代入（9）式得

化简得

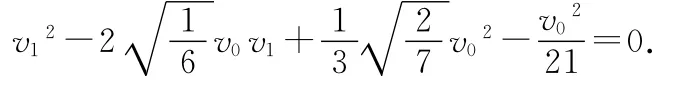
即可得到飞行器与小行星碰撞后的速率为

现在判断飞行器在这个速度下能不能飞出太阳系.假设飞行器不能飞出太阳系，则其近日点速度与轨道半长轴、半焦距的关系依然满足（3）式，即

考虑到此时飞行器在近日点，且其离日距离为6R，即a－c＝6R，将此式与（10）式一起代入（11）式可得

化简可得

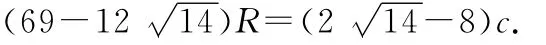
可得c≈－46.64R.

显然，一个正常椭圆的半焦距不可能取负值，即飞行器运行轨道不是椭圆，则飞行器一定可以飞出太阳系.

（2）在上述方法中，飞行器从发动机得到的能量为

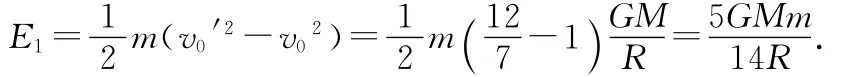
如果不用上述方法，飞行器要刚刚飞离太阳系，相当于椭圆半长轴与半焦距都趋向于无穷大，但两者之差为R，利用（3）式，可得飞行器要获得的动能为

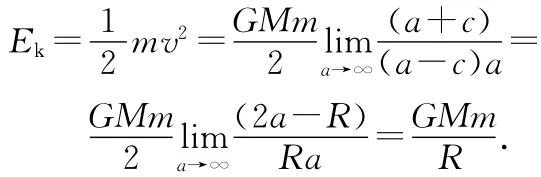
飞行器从发动机得到的能量为

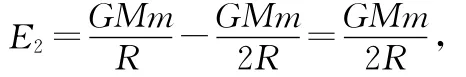
即可得

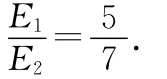
例3.（第20届决赛第2题）一人造地球卫星绕地球做椭圆运动，地心是椭圆的一个焦点，在直角坐标系中，椭圆的轨迹方程为

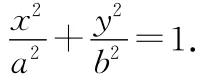
a、b分别为椭圆的长半轴和短半轴，为已知常数.当该卫星在轨道远地点时，突然以很大的能量沿卫星运动方向从卫星上发射出一个质量为m的太空探测器，这探测器在地球引力作用下做双曲线运动，此双曲线的焦点位于地心，实半轴的长度正好等于原来椭圆远地点到地心的距离.试问在发射时，给探测器的能量为多大？设地球质量为mE、万有引力常量为G为已知，不计地球以外星体的影响.

解析：先由（4）式可得远地点速度为

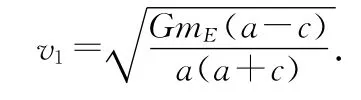
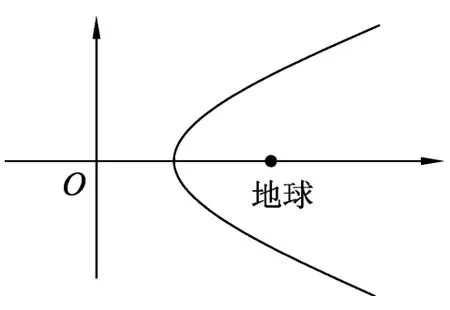
图2

探测器在远地点时，其离地球距离为A＝a＋c.当探测器突然加速做双曲线运动时，双曲线的焦点位于地心，实半轴的长度正好等于原来椭圆远地点到地心的距离，则半焦距等于椭圆远地点到地心的距离的两倍.可以移动直角坐标系，使此时探测器与地球的位置坐标分别为（A，O）和（C，O），其中A＝a＋c，C＝2（a＋c）.

则在0时刻，其速度为

其加速度为

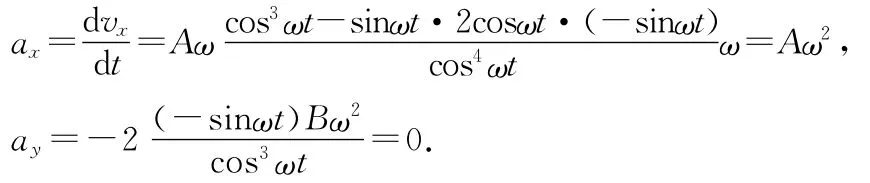
则可得双曲线顶点的曲率半径为

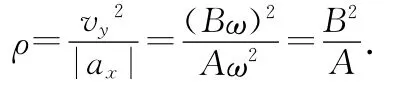
因发射时探测器势能来不及变化，故动能改变量就是获得的总能量