冻土地区高速铁路软土路基沉降预测模型研究
2014-07-25罗海风
邓 锐 李 波 罗海风
(中铁西南科学研究院有限公司, 四川成都 610000)
冻土地区高速铁路软土路基沉降预测模型研究
邓 锐 李 波 罗海风
(中铁西南科学研究院有限公司, 四川成都 610000)
对几种常用沉降预测模型进行了对比分析,介绍了组合预测模型的构建思路及预测效果的评价标准,建立了冻土地区路基组合预测模型。
冻土地区 软土路基 沉降预测 组合预测模型
1 常用沉降预测精度对比
沉降观测工作是测量中变形观测最基本的工作之一。随着科技的不断进步和众多专家学者的不断研究与探索,目前已建立了比较完善的沉降观测体系。常用的沉降预测模型主要有以下几种:规范双曲线模型、修正双曲线模型、泊松曲线模型、三点法模型、Asaoka法模型和灰色系统GM(1,1)模型[6-7],预测精度的评价主要有以下两个方面:相关系数分析与预测误差分析,根据“哈齐客运专线”某区段实测的数据,对以上模型的预测精度进行分析。
1.1 相关系数分析
相关系数是高速铁路沉降观测评估分析一个很重要的技术指标,也是检查沉降观测数据质量的重要手段[8]。本文采取若干个观测断面的沉降观测数据作为实验数据,通过分析并计算出各模型的相关系数。规范双曲线法的曲线回归的相关系数为64.4%;修正双曲线法的曲线回归的相关系数为63.2%;泊松曲线法的曲线回归的相关系数为95.4%;三点法的曲线回归的相关系数为93.1%;Asaoka法的曲线回归的相关系数为89.7%;灰色系统GM(1,1)模型曲线回归的相关系数为40.2%。由此可见,泊松曲线法、三点法和Asaoka法曲线回归的相关系数都比较大,规范双曲线法和修正双曲线法的相关系数次之,灰色系统GM(1,1)模型的相关系数较低。
1.2 预测误差分析
预测误差也是高速铁路沉降观测评估分析一个很重要的技术指标。它是检验沉降预测质量的重要手段,预测误差的大小将直接影响路基的工后沉降量的判定。表1列出了上述监测断面的各个预测模型曲线拟合的预测误差范围(△指预测误差)。
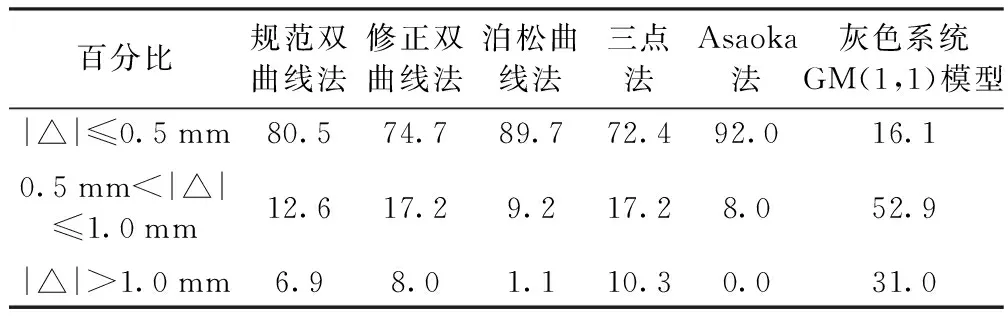
表1 各个预测方法曲线回归的预测误差统计 %
由表1可见,对该段测区而言,泊松曲线法和Asaoka法曲线回归的预测误差比较小;规范双曲线法、修正双曲线法和三点法的预测误差次之;灰色系统GM(1,1)模型的预测误差最大。
通过对以上预测模型相关系数和预测误差进行综合比较,可知泊松曲线法和Asaoka法在该段区域内的预测效果优于其他几种预测模型。
2 组合预测模型介绍
现实生活中,一个问题常常有不同的解决方法,高速铁路软土路基沉降预测也一样,有很多种预测模型可供选择使用,但是各个预测方法将给出不相同的预测结果,预测精度也不尽相同。如果按照预测精度的好坏,从多种预测方法中选择预测精度最好的一个,而把预测误差较大的预测方法完全抛弃,这样并不是提高预测精度的办法,反而会失去一些有用的信息,造成信息的浪费。比较科学的方法是:把各个不同的预测方法通过某种方式进行组合搭配,也就是组合预测模型。组合预测方法就是针对同一个问题,综合分析各种常用预测模型的预测信息,把两种或两种以上的预测模型按照适当的权重比例组合起来,从而得到组合预测模型;组合预测方法的关键问题是各个常用预测模型加权系数的确定,要使得组合预测方法达到最好的预测效果;组合的主要目的是综合各个模型的优点,避其不足,尽可能地提高预测精度。一般地,组合预测方法有两种基本形式。
等权组合:将各个预测模型的预测值按相同的权系数组合,得到新的预测值。
不等权组合:给各个预测模型的预测值赋予的权系数不相同,组合成新的预测值。
2.1 组合预测模型的构建思路
如果一个单预测模型含有待预测系统的独立信息,即使它的预测精度比较差,但是当它与另一个较好的单预测模型组合后,就会有可能提高组合模型的预测精度。其数学表达形式如下
(t=1,2,…,n)
上式被称为B-G模型。其中,m为单预测模型的个数;n为实测数据的个数;fit(i=1,2,…,m;t=1,2,…,n)为第i种单预测模型在t时刻的预测值,ki(i=1,2,…,m)为第i种单预测模型在线性组合预测模型中的权重,为保证组合预测的无偏性,各个权重系数需满足:k1+k2+…+km=1,yt为线性组合预测模型在t时刻的组合预测值。
组合预测模型的一般建模步骤如图1所示。
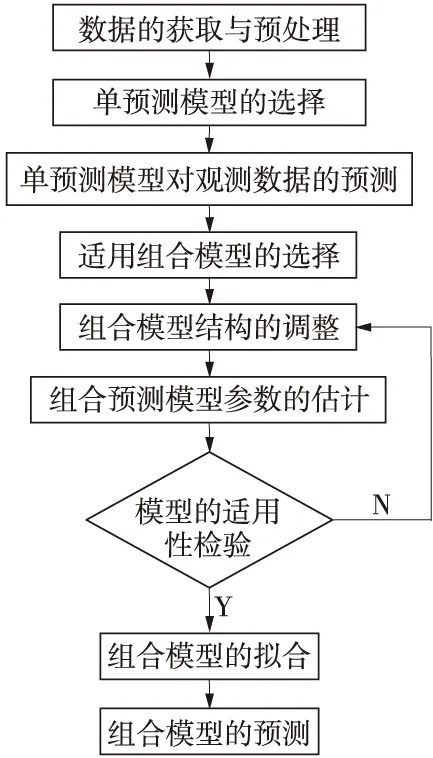
图1 组合预测模型的建模步骤
2.2 组合预测模型运用需要考虑的问题
(1)所选各个单预测模型都能独立对观测数据进行预测分析,并能达到一定的预测效果。
(2)所选单预测模型能够满足组合预测模型的应用条件。
(3)所选单预测模型对观测数据的要求或假设条件应大致相同。
(4)所选单预测模型的复杂程度和数据处理的难易程度要适度。
(5)单预测模型个数的确定要合理。
(6)选择合适的权系数求解方法。
2.3 组合预测模型预测效果的评价标准
根据预测效果的评价原则和惯例,常采用下面五个指标来评价组合预测模型的预测效果:
(1)平方和误差
(2)均方误差
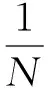
(3)平均绝对误差
(4)均方百分比误差
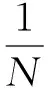
(5)平均绝对百分比误差
一般情况下,通过满足“预测误差平方和最小准则”和“预测误差绝对值最小准则”来衡量模型的预测精度。
预测误差平方和最小准则:假定某一预测对象的指标序列{xt,t=1,2,…,N},存在m种单预测模型对其进行预测分析,设第i种单预测模型在t时刻的预测值为xit,i=1,2,…,m;t=1,2,…,N,称eit=(xt-xit)为第i种单预测模型在t时的预测误差。
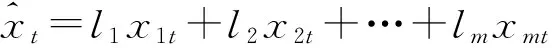
设J1为组合预测模型预测误差平方和,其表达式为
因此,以预测误差平方和最小准则的线性组合预测模型为下面方程式的最优化问题
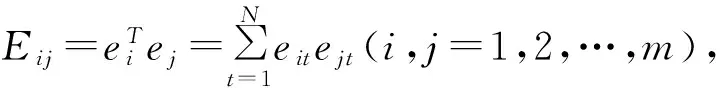
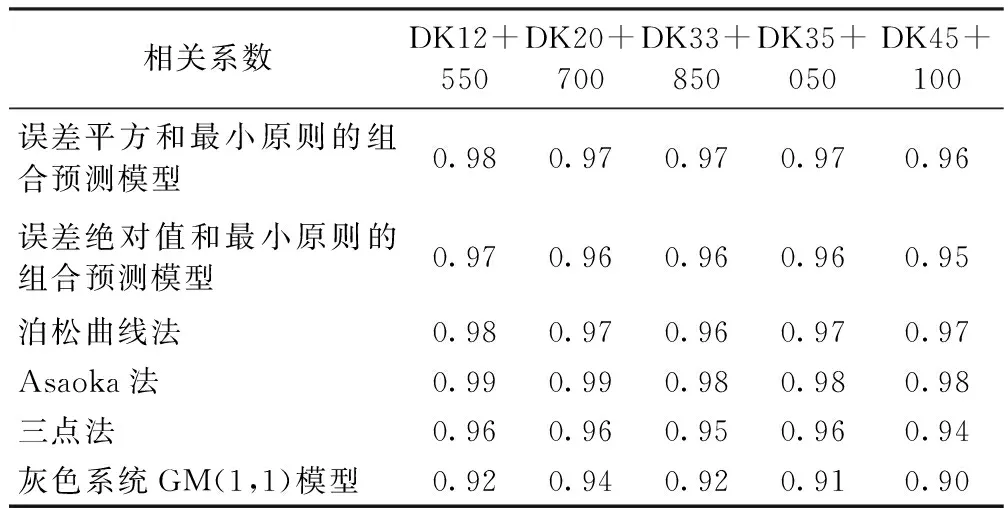
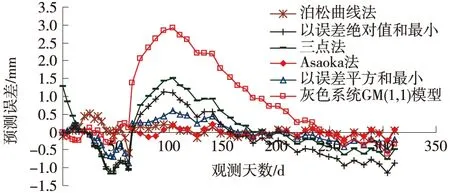
假设m(m 上面的公式可以转化为以下矩阵形式 模型的最优解和目标函数最优解 预测误差绝对值和最小准则: 假设F表示组合预测模型的预测误差绝对值和,则有 可以得到以误差绝对值和最小准则的最优线性组合预测模型 则可以将预测问题转换为线性规划求解最优解的问题,假设 ; 这样就转换成一个线性规划问题,用现有的线性规划软件即可求解。 结合冻土地区的实验数据,论证三点法和灰色系统GM(1,1)的组合预测模型在满足预测误差平方和最小准则和以预测误差绝对值和最小准则前提下的可行性,并与其他基本预测模型进行精度对比。 3.1 相关系数对比 这里仍然以前面所选测区的观测数据作为考查对象,从误差平方和最小准则和误差绝对值和最小准则两个方面考虑,将三点法-灰色系统GM(1,1)组合预测模型与泊松曲线法、Asaoka法、三点法、灰色系统GM(1,1)模型的预测结果相比较,表2给出了6种不同预测方法下的曲线回归分析的相关系数大小。 分析表2可以得出,除了灰色系统GM(1,1)模型曲线回归的相关系数不能完全满足《评估指南》中相关系数不小于0.92的要求之外,其他几种预测模型曲线回归的相关系数都能满足要求;以误差平方和最小的三点法-灰色系统GM(1,1)模型的组合预测方法比以误差绝对值和最小的三点法-灰色系统GM(1,1)模型的组合预测方法的曲线回归的相关系数大,其中以误差平方和最小的三点法-灰色系统GM(1,1)模型的组合预测方法比三点法和灰色系统GM(1,1)模型的曲线回归的相关系数大,以误差绝对值和最小的三点法-灰色系统GM(1,1)模型的组合预测方法与三点法的相关系数相当,比灰色系统GM(1,1)模型的相关系数大。 表2 5个断面在6种不同预测方法下的曲线回归分析的相关系数 3.2 预测误差对比 图2为某一断面在6种不同预测方法下的预测误差。 图2 DK12+550断面在6种不同预测方法下的预测误差 分析上图可知,除了灰色系统GM(1,1)模型的预测误差较大之外,其他几种预测模型的预测误差相对较小;以误差平方和最小的三点法-灰色系统GM(1,1)模型的组合预测方法、Asaoka法、泊松曲线法的预测误差最小,以误差绝对值和最小的三点法-灰色系统GM(1,1)模型的组合预测方法和三点法的预测误差次之。 从以上的介绍和对实测数据的分析,可以得出如下基本结论: 从曲线回归的相关系数大小和预测误差大小来看,以误差平方和最小的三点法-灰色系统GM(1,1)模型的组合预测方法的预测效果明显优于三点法与灰色系统GM(1,1)模型;以误差绝对值和最小的三点法-灰色系统GM(1,1)模型的组合预测方法的预测效果比灰色系统GM(1,1)模型好很多,但与三点法的预测效果相当。 从曲线回归的相关系数大小和预测误差大小来看,以误差平方和最小的三点法-灰色系统GM(1,1)模型的组合预测方法比以误差绝对值和最小的三点法-灰色系统GM(1,1)模型组合预测方法的预测效果要好,与泊松曲线法、Asaoka法的预测效果基本相同。 对于哈齐铁路客运专线软土路基“沉降变形量级小、相对波动大”的情形而言,推荐优先考虑全过程的预测精度高的沉降预测方案,即首选以误差平方和最小的三点法-灰色系统GM(1,1)模型的组合预测方法和泊松曲线法对沉降全过程进行预测分析,其次选择Asaoka法对恒载后的沉降观测数据进行预测分析,并和前两种预测结果进行对比。也可以运用三点法、修正双曲线法等预测方法进行预测,综合考虑各个预测结果,这样会有更好的效果。 本文基于冻土地区高速铁路软土路基的沉降进行预测模型的选取,对冻土地区其他软土路基的沉降预测模型的选取具有一定的参考价值。 [1] 张丽丽.软土路基沉降计算及预测方法研究[D].西安:西安建筑科技大学,2006 [2] 刘升传,曹渊.新建铁路软土路基沉降规律研究[J].铁道工程学报,2010,5(5):1-3 [3] 李涛,张仪萍,张土乔.软土路基沉降的优性组合预测[J].岩石力学与工程学报,2005,24(18):3282-3286 [4] 雷康.软土路基沉降的组合预测方法研究[D].长沙:长沙理工大学,2010 [5] 孟庆新.软土路基变形分析与沉降预测[D].石家庄:河北工业大学,2006 [6] 赵明华,刘煜,曹文贵.软土路基沉降发展规律及其预测[J].中南大学学报:自然科学版,2004,35(1):157-161 [7] 许俊超.软土地基沉降预测方法探讨[J].铁道勘测与设计,2008(4) [8] 中华人民共和国铁道部.客运专线无砟轨道铁路工程测量暂行规定[S].北京:中国铁道出版社,2006 [9] 何飞.高速铁路路基基础工后沉降预测的相关研究[D].成都:西南交通大学,2009 [10]刘志明.客运专线地基沉降计算、预测方法研究[D].成都:西南交通大学,2009 ResearchofPredictionModelofHighspeedRailwaySoftSoilSubgradeSettlementinFrozenEarthArea DENG Rui LI Bo LUO Hai-feng 2014-04-24 邓 锐(1987—),男,2012年毕业于中国地质大学(武汉)遥感科学与技术专业,助理工程师。 1672-7479(2014)04-0024-04 TU433 : A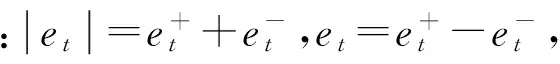
3 冻土地区路基组合预测模型的建立
4 结论
