雷达机动目标的自适应跟踪算法*
2014-07-25李峻年
李峻年 白 颖
(1.海军驻葫芦岛431军代室 葫芦岛 125001)(2.92941部队94分队 葫芦岛 125001)
雷达机动目标的自适应跟踪算法*
李峻年1白 颖2
(1.海军驻葫芦岛431军代室 葫芦岛 125001)(2.92941部队94分队 葫芦岛 125001)
机动目标跟踪一直是雷达目标跟踪的重点难点,论文建立了一种当前统计模型的目标运动模型,给出了概率密度以及非零均值目标加速度随机过程数学表达式,结合基本Kalman滤波,建立了基于该模型的机动目标跟踪自适应算法。最后针对实际目标机动情况,对其进行仿真计算,仿真结果证明,该算法具有良好的跟踪性能。
机动目标跟踪; 非零时间相关模型; 当前概率密度; 自适应
ClassNumberTJ391
1 引言
机动目标跟踪算法的两大要素为: 1)建立较为合理的机动目标运动模型, 2)选择正确的滤波模型。目标机动模型众多,不少学者对此进行了大量研究,建立了众多模型[1~6],总的来看,大致可分为“全局”统计模型和“当前”统计模型,全局统计模型包括Sing模型、半马尔可夫模型和Noval统计模型,它们的共同点是考虑了目标机动变化的可能性,适合于各种情况和各种类型的目标机动,但在该模型中每一种具体情况下的战术情况考虑不够,即机动模型精度不够。相反,我们应该关心的是每一种具体情况下的每一种具体机动,因此本文提出了一种基于“当前”统计模型的目标运动模型,并结合Kalman滤波算法,建立了机动目标自适应跟踪算法。
2 当前统计模型
2.1 加速度的“当前”概率密度
机动目标跟踪的主要问题之一是建立未知的加速度模型。此问题由两部分构成,其一是表征目标机动的随机过程性,即这种随机过程是白色的,还是时间相关的;其二涉及到运动加速度的特定概率密度函数[7~8]。对于第一部分,许多学者更倾向于把目标看成是相关随机过程。而对概率密度而言,可认为当目标正以某一加速度机动时,它在下一瞬时的加速度是有限的,而且只能在“当前”加速度的邻域内。因此在描述加速度的概率密度时,机动加速度的取值范围可以大大减小,并且不用考虑机动加速度取值的所有可能性,在每一瞬间,一种时变的机动加速度概率密度函数将对应于目标“当前”加速度的变化[9]。基于以上考虑,可选用修正的瑞利密度函数作为当前统计模型的概率密度函数,为
(1)
其中amax>为已知的目标加速度上限,a为目标随机加速度,μ>0为一常数。
a的均值和方差为
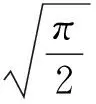
(2)
(3)
当目标的“当前”加速度为负时,概率密度函数为
(4)
a的均值和方差为
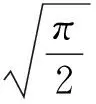
(5)
(6)
当目标的“当前”加速度为零时,概率密度函数为
P(a)=δ(a)
(7)
式中δ(·)为狄拉克函数。在上述概率密度函数中,每一瞬时机动加速度的概率密度是不同的,一旦“当前”加速度值被给定,加速度概率密度函数便完全确定。
2.2 机动加速度的非零均值时间相关模型
在“当前”统计模型概念条件下,当目标正以某一加速度机动时,加速度采用零均值模型是不符合实际的,因此可假设目标加速度是非零均值的时间相关随机过程,即:
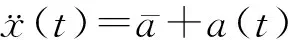
(8)

(9)
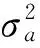
通过Wiener-Kolmogorov的白化过程[10~11],式(8)可表示为一阶平稳相关的Markov过程:

(10)
其中α是机动时间常数的倒数。
3 基于“当前”统计模型的自适应卡尔曼滤波算法
3.1 自适应卡尔曼滤波算法
设采样周期为T,根据以上对零均值相关运动模型的描述,得到该模型的目标状态方程:

(11)

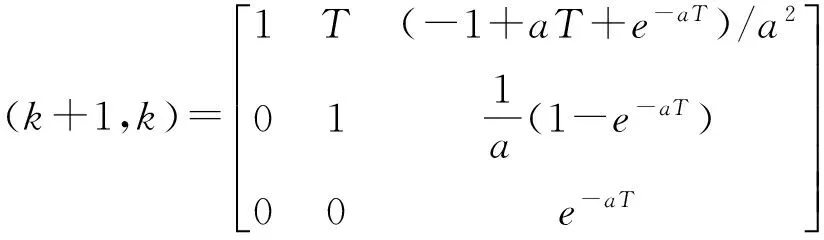
(12)
(13)
W(k)为离散时间白噪声序列,方差为
(14)
QM是与a和周期T有关的常量矩阵[5]。
设目标的观测方程为
Y(k)=H(k)X(k)+V(k)
(15)
其中H(k)=[1,0,0],V(k)为高斯观测噪声,其均值为零,方差为R(k)。
采用状态方程式(11)和式观测方程(15),利用标准卡尔曼滤波递推关系,得到基于“当前”统计运动模型的机动目标跟踪算法的基本过程,如下:

(16)
P(k+1/k)=φ(k)P(k/k)φT(k)+Q(k)
(17)
K(k+1)=P(k+1/k)HT[H(k+1)P(k+1/k)HT×(k+1)+R(k+1)]-1]
(18)
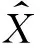
(19)
P(k+1/k+1)=[I-K(k+1)H(k+1)]P(k+1/k)
(20)

(21)
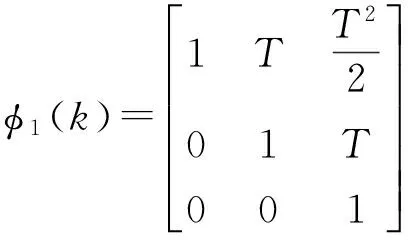

(22)
当“当前”加速度为负时,有:
(23)
3.2 自适应滤波系统
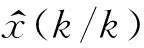
(24)
当“当前”加速度为负时,有:
(25)

图1 自适应滤波系统
4 仿真结果与分析
为了验证该算法的有效性,下面分别用全局统计模型Singer模型和当前统计模型两种方法对典型目标机动情况进行仿真,对比分析。仿真中,假设观测噪声方差与目标距离的平方成正比,即观测噪声:
V(k)=(βx(k)+Δx0)ω(k)
(26)
式中β为相对误差系数,Δx0为固定测量误差,ω(k)是均值为零,方差为1的正态分布随机数,观测噪声方差为
R(k)=(βx(k)+Δx0)2·E[ω2(k)]
(27)
仿真中参数取值为Δx0=30km,β=0.01,α=0.1,T=1。假设目标作恒加速运动,其加速度为20m/s2,仿真曲线如图2、图3所示。实线段表示基于当前统计模型的跟踪结果,虚线段表示Singer模型的跟踪结果。从仿真结果可以看到目标作等加速度运动时,Singer模型无法给出正确的加速度估计。

图2 机动目标加速度仿真结果

图3 机动目标速度仿真结果
5 结语
仿真结果证明,本文提出的基于当前计模型的机动目标自适应跟踪算法能更好地反映目标的实际机动情况,它的跟踪机动目标能力更强,效果更佳。
[1]肖雷,刘高峰,魏建仁.几种机动目标运动模型的跟踪性能对比[J].火力与指挥控制,2004(1):10-13.
[2]高羽,张建秋.机动目标的多项式预测模型及跟踪算法[J].航空学报,2009,30(8):1479-1489.
[3]张强,孙尧,万磊,等.多普勒测速声呐的自适应Kalman滤波算法[J].哈尔滨工程大学学报,2011,12(32):1534-1537.
[4]陈莉,徐庆民.一种新的机动目标跟踪的多模型算法[J].山西国防工业职业技术学院学报,2008(2):18-21.
[5]徐吉莉,高立娥,张超.水下目标运动参量估计及仿真技术[C]//2012中国西部声学学术交流会议论文集,2012(2):98-102.
[6]RA Singer Estimating Optimal Tracking Filter Performance of Manned Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems,1970,6(4):473-483.
[7]周宏仁.机动目标“当前”统计模型与自适应跟踪算法[J].航空学报,1983,4(1):73-86.
[8]曾劲松,朱岩,姚善粱.软件声纳的目标自动跟踪系统建模[J].现代电子技术,2010(14):73-75.
[9]冯道旺,李腾,黄知涛.平方根二阶EKF及其在目标运动分析中的应用[J].系统工程与电子技术,2009,31(9):2101-2105.
[10]刘福声,罗鹏飞.统计信号处理平[M].长沙:国防科技大学出版社,1999:156-187.
[11]白士君,凌国民.水声网络探测节点的一种运动目标参数估计算法[J].舰船电子工程,2010,30(5):186-188.
AdaptiveTrackingAlgorithmofRadarManeuveringTarget
LI Junnian1BAI Ying2
(1. Navy Representative Office in 431 Plant, Huludao 125001)(2. Unit 94, No. 92941 Troops of PLA, Huludao 125001)
The maneuvering mobile target tracking has been the most important and difficult problems in the radar data processing. First a current statistical model of maneuvering target is set up in the paper. Then the probability density and the algorithm of random process about the nonzero time related model are presented. Combing the Kalman Filter, the adaptive tracking algorithm of maneuvering target is set up. Finally the algorithm is simulated, and the simulating result proves the effectiveness of the algorithm.
the maneuvering target track, nonzero time related model, current probability density, adaptive
2013年10月7日,
:2013年11月27日
李峻年,男,工程师,研究方向:水下武备总体研究。白颖,女,工程师,研究方向:舰炮系统试验与研究。
TJ391DOI:10.3969/j.issn1672-9730.2014.04.009
