有限域GF(2n)上Hadamard型MDS矩阵研究*
2014-07-25
(中国船舶重工集团公司第七二二研究所 武汉 430079)
有限域GF(2n)上Hadamard型MDS矩阵研究*
刘丽辉徐林杰张祖平李艳萍
(中国船舶重工集团公司第七二二研究所 武汉 430079)
论文研究了有限域GF(2n)上Hadamard矩阵的性质,证明了Hadamard矩阵成为MDS矩阵及对合MDS矩阵的所需满足的必要条件。特别地,当矩阵阶数为4时,证明了充要条件。改进了4阶及8阶Hadamard型MDS矩阵的生成算法。
Hadamard矩阵;MDS矩阵;对合
ClassNumberTP301.6
1 引言
MDS矩阵作为一种最优扩散映射,广泛应用于AES、CLEFIA[1]、Twofish[2]及FOX[3]等算法的扩散层设计中。常见扩散层设计中的MDS矩阵一般是循环矩阵、Hadamard矩阵、Cauchy矩阵[4]等类型的矩阵。Cauchy矩阵因矩阵元素汉明重量较大,不利于算法在各种平台上的实现,因此在算法设计中并不常用;如果一个循环矩阵是MDS矩阵,则该矩阵一定不是对合的[5],因此,循环矩阵的应用具有局限性;Hadamard矩阵元素汉明重量较小,并且可以是对合的MDS矩阵,具有易于实现的特点。因此,深入研究Hadamard矩阵型MDS矩阵的性质及产生方法,对密码算法设计具有重要意义。随机生成并检验的MDS矩阵生成方法效率较低。文献[6]通过对有限域GF(2n)上Hadamard矩阵生成条件加以限制,提升了MDS矩阵的生成效率,但是效率提升有限。本文通过对Hadamard矩阵性质的深入研究,极大地提升了Hadamard型MDS矩阵的生成效率。
2 预备知识
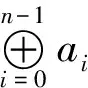
定义1[7]设A=(ai,j)2m×2m是GF(2n)上的2m×2m矩阵,如果当0≤i,j≤2m-1时,均有ai,j=a0,i⊕j,则称A为有限域GF(2n)上的一个Hadamard矩阵,并简记为A=Had(a0,0,a0,1,…,a0,2m-1)。
性质1 有限域GF(2n)上的Hadamard矩阵是对称矩阵。
证明:设A=Had(a0,0,a0,1,…,a0,2m-1),任取0≤i,j≤2m-1,则
ai,j=a0,i⊕j=a0,j⊕i=aj,i,所以矩阵A为对称矩阵,证毕。
定义2[8]设f(x)=Ax,A是GF(2n)上的m×m矩阵,x={x1,x2,…,xm}为(GF(2n))m上的m维列向量,Wh(x)表示非零xi(1≤i≤m)的个数。则称:

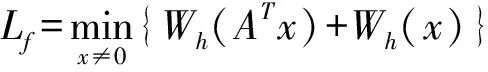
显然f的差分分支数与线性分支数的最大值为m+1。
分支数可以衡量有限域上线性矩阵密码学性质好坏,当f的差分分支数与线性分支数都达到最大值时,则称矩阵A为MDS矩阵。当矩阵A为MDS矩阵时,变换f为最优的扩散变换。
由Hadamard矩阵的对称性,结合差分分支数与线性分支数的定义可有如下推论:
推论1 有限域GF(2n)上Hadamard矩阵的差分分支数和线性分支数相等。
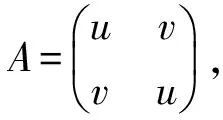
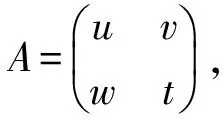
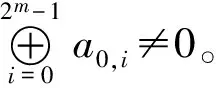
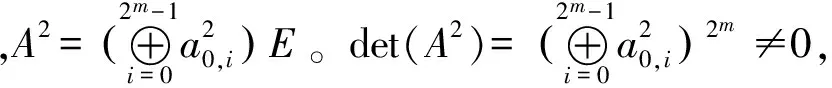
定理2 有限域GF(2n)上的MDS矩阵的逆矩阵也是MDS矩阵。
证明:设矩阵A是有限域上的MDS矩阵,A-1表示矩阵A的逆矩阵,则根据线性分支数的定义有min{Wh(x)+Wh(A-1x)}=min{Wh(A(A-1x))+Wh(A-1x)}=m+1,即A-1的线性分支数达到最大,同理可证A-1的差分分支数也达到最大,因此A-1是MDS矩阵。
性质3 有限域GF(2n)上的Hadamard矩阵的逆矩阵仍是Hadamard矩阵。
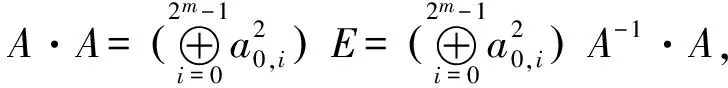
根据定理3与Hadmard矩阵的性质3有如下定理:
定理3 有限域GF(2n)上Hadamard型MDS矩阵的逆矩阵是Hadamard型MDS矩阵。
3 有限域GF(2n)上的Hadamard型MDS矩阵
有限域上Hadamard矩阵一般通过随机方式生成,通过分支数的定义可以判定该矩阵是否为MDS矩阵。但该方法计算量较大,通常使用如下引理检验已知矩阵是否为MDS矩阵。
引理1[5]有限域GF(2n)上的矩阵是MDS矩阵的充要条件是该矩阵的所有子方阵都是非退化的。
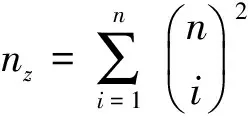
定理4[6]有限域GF(2n)上的Hadamard矩阵Had(a0,0,a0,1,…,a0,2m-1)是MDS矩阵的必要条件是a0,0,a0,1,…,a0,2m-1两两不同且不为0。
根据定理4生成的Hadamard矩阵,第一行元素均不为零,则该Hadamard矩阵的矩阵元素均不为零,即矩阵的1阶子阵均非退化;矩阵的第一行元素互不相同,则矩阵的一些2阶方阵非退化。定理4通过限定Hadamard矩阵的生成条件,使得生成矩阵的非退化子方阵的个数增多。
本文研究了有限域的Hadamard矩阵的性质后,在文献[5]的基础上进一步增加了在限定条件下生成矩阵的非退化子方阵的个数。
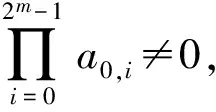
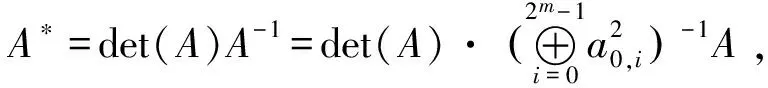
结合引理1与定理4有如下定理:
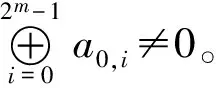
与定理4相比,定理6仅增加一个限制条件,即要求矩阵的第一行元素和不为零,则此时该Hadamard矩阵非退化,且该Hadamard矩阵的所有三阶子方阵也均为非退化矩阵。
对于已知的n阶方阵,所有子方阵的个数是确定的,如果需要判断该矩阵是否为MDS矩阵,若非退化子方阵的个数越多,即非退化子方阵个数的下界越大,则需测试的子方阵个数越少,这就提高了判断已知矩阵是否为MDS矩阵的效率。
表1列举了四种2m(m=0,1,2,3)阶矩阵的所有子方阵的个数和不同方法下非退化子方阵个数的下界。
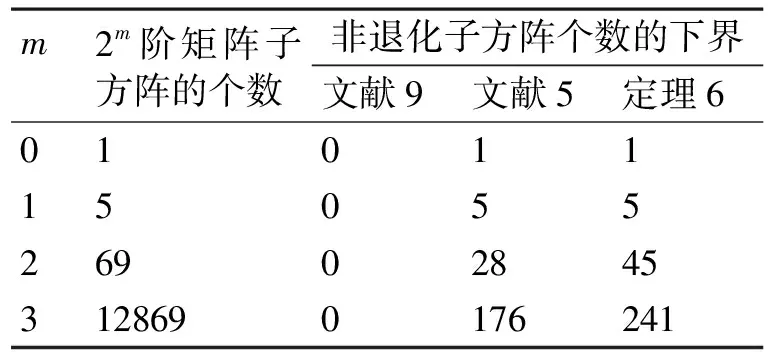
表1 2m阶矩阵非退化子方阵个数下界比较
3.1 有限域GF(2n)上4阶Hadamard型MDS矩阵
以上讨论了2m阶Hadamard矩阵成为MDS矩阵的必要条件。根据定理6的限制条件生成的4阶Hadamard矩阵,具有该矩阵,1阶子方阵,3阶子方阵及一些2阶子方阵非退化的特点。补充以上条件,可得到4阶Hadamard矩阵是MDS矩阵的充要条件。
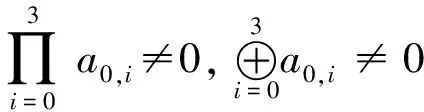
证明:此时只需考虑2阶子式。对任意的2阶子式
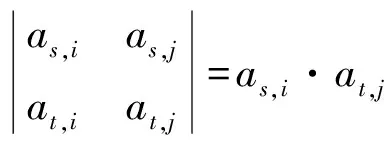
上述定理指出了生成Hadamard型MDS矩阵的充要条件,实际的Hadamard型MDS生成算法中,判断条件可以进一步减少。由于Hadamard矩阵的许多子矩阵是等价的,如:
=a0·a3⊕a1·a2
因此,Hadamard型MDS矩阵生成算法中只需判断其中一个矩阵即可。更实用的筛选4阶Hadamard型MDS矩阵的算法如下:
算法1
step1.定义有限域GF(2n)的运算,加法,乘法;
step2.选取4个互不相同且不为0的元素0
step3.如果a0⊕a1⊕a2⊕a3=0,返回step2;
step4.计算a0a3⊕a1a2,a0a1⊕a2a3或a0a2⊕a1a3,若有结果为0,返回step2;
step5.由a0,a1,a2,a3生成4阶Hadamard矩阵;
step6.输出矩阵A=Had(a0,a1,a2,a3)。
则输出矩阵A即为Hadamard型MDS矩阵。
算法1是一种4阶的Hadamard型MDS矩阵的生成方法,与引理1中需测试69个子方阵相比,通过定理6的限制条件产生Hadamard矩阵,仅需测试3个2阶方阵是否非退化。极大地简化了Hadamard型MDS矩阵生成的判定条件与计算过程,大大的提高了Hadamard型MDS矩阵的生成效率。
3.2 有限域GF(2n)上8阶Hadamard型MDS矩阵
同4阶Hadamard型MDS矩阵相比,8阶Hadamard型MDS矩阵的生成需要测试的子式个数是惊人的,需要测试更多的矩阵才可能产生一个符合条件的矩阵。若能根据较小阶的MDS矩阵生成一个高阶的MDS矩阵是个一个很好的选择。
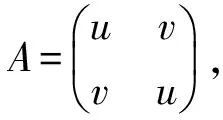
可结合算法1中的4阶Hadamard型MDS矩阵生成算法与定理8,构造8阶Hadamard型MDS矩阵生成算法。如下:
算法2
step1.定义有限域GF(2n)的运算,加法,乘法;
step2.根据算法1选取u0,u1,u2,u3,生成Hadamard型MDS矩阵U;
step3.根据算法1选取v0,v1,v2,v3(与u0,u1,u2,u3两两不同)生成Hadamard型MDS矩阵V;
step5.由U、V生成8阶Hadamard矩阵;
step6.计算该Hadamard矩阵的k阶子式2≤k≤2m-2,若有k阶子式为零,返回step3;
则输出矩阵即为8阶Hadamard型MDS矩阵。
由算法1可知,生成若干个4阶的Hadamard型MDS矩阵是容易的,根据Hadamard矩阵的性质,由任意矩阵元素互不相同的两个4阶的Hadamard型MDS矩阵生成8阶的Hadamard是简单的。通过定理8的限制条件产生的Hadamard矩阵的非退化子方阵的个数已经达到340个,需判断的子方阵的个数进一步减少,进一步提升了Hadamard型MDS矩阵的生成效率。
4 有限域GF(2n)上对合的Hadamard型MDS矩阵
SP结构是目前广泛适用的一种分组密码整体结构,如AES、ARIA[10]、PRESRNT[11]等分组密码都采用此种结构。该种结构可以得到更快速的扩散,使得密码的输入输出更为复杂。但是,SP结构的密码算法需要对子模块进行限制,才能保证算法的加解密相似,如AES算法的扩散层中使用了循环矩阵,虽然该矩阵是MDS矩阵,但是由于该矩阵不是对合的,所以该算法的解密过程中使用了与加密过程中不同的循环矩阵。如果扩散层的MDS矩阵是对合的,则可保证该算法的加解密相似。
文献[5]指出,循环型MDS矩阵一定不是对合矩阵,循环矩阵的这一性质限制了循环矩阵在SP结构分组密码算法中的广泛应用。而由于有限域GF(2n)上Hadamard矩阵结构与性质的特殊性,存在很多对合的矩阵。
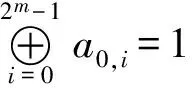
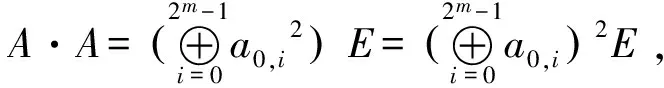
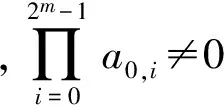
特别地,对4阶Hadamard矩阵有:
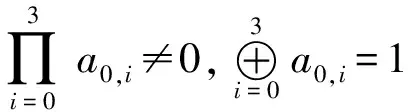
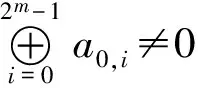
5 结语
本文研究了有限域上Hadamard矩阵的一些性质,结合密码学知识,研究了2m阶Hadamard矩阵成为MDS矩阵,对合的MDS矩阵的必要条件。并针对4阶MDS矩阵的特点,证明了4阶Hadamard矩阵成为MDS矩阵、对合MDS矩阵的充要条件。当矩阵阶越大,需判断条件越多,限制了更高阶MDS矩阵的生成,本文改进了8阶Hadamard矩阵的生成方法,但能否找到8阶Hadamard矩阵是MDS矩阵以及对合的MDS矩阵的充要条件是我们以后的研究工作。
[1]T. Shirai, K. Shibutani, T. Akishita, et al. The 128-bit Blockcipher CLEFIA[C]//FSE’07, LNCS 4593, Springer Verlag,2007:181-195.
[2]Schneier B, Kelsey J, Whiting D. The Twofish Encryption Algorithm:A 128-bit Block Cipher[M]. New York:John Wiley and Sons, Inc,1999:7-11.
[3]Junod, P., Vaudenay, S. FOX:A new family of block ciphers[C]//Handschuh, H., Hasan, M.A. (eds.)SAC 2004. LNCS, Springer, Heidelberg,2004,3357:114-129.
[4]A. Youssef, S. Mister, S. Tavares. On the Design of Linear Transformations for Substitution-Permutation Encryption Networks[C]//Workshop on Selected Areas in Cryptography-SAC’97, Ottawa,1997:164-171.
[5]王念平,金晨辉,余昭平.对合型列混合变换的研究[J].电子学报,2005,33(10):1917-1920.
[6]崔霆,金晨辉.对合Cauchy-Hadamard型MDS矩阵的构造[J].电子与信息学报,2010,32(2):500-503.
[7]Xiao L, Heys H. Hardware design and analysis of block cipher components[C]//Proceedings of the 5th International. Conference on Information Security and Cryptology-ICISC’02,2003,2587:164-181.
[8]J Daemen. Cipher and Hash Function Design Strategies Based on Linear and Differential Cryptanalysis[D]. Leuven:K U Leuven,1995.
[9]Joan Daemen, Lars Knudsen, Vincent Rijmen. The Block Cipher Square[C]//Fast Software Encryption(FSE),1997:149-165.
[10]Kwon, D, Kim, J, Park, S, et al. New Block Cipher:ARIA[C]//Lim, J.-I., Lee, D.-H.(eds.)ICISC 2003. LNCS, Springer, Heidelberg,2004,2971:432-445.
[11]Bogdanov, A., Knudsen, L. R., Leander, G., et al. PRESENT:An ultra-lightweight block cipher[C]//Paillier, P., Verbauwhede, I. (eds.)CHES 2007. LNCS, Springer, Heidelberg,2007:450-466.
InvestigateforMDSMatrixofHadamardTypeonFiniteFields
LIU Lihui XU Linjie ZHANG Zuping LI Yanping
(No. 722 Research Institute of CSIC, Wuhan 430079)
In this paper, the character of Hadamard Matrices is investigated, and the necessary condition of Hadamard matrix being MDS matrix and involution MDS matrix is given. In special, the necessary and sufficient condition for 4-order matrix are illustrated. Additionally, the generating algorithms are improved for 4-order and 8-order MDS matrix of Hadamard type.
Hadamard matrix, MDS matrix, involution
2013年11月8日,
:2013年12月27日
刘丽辉,女,硕士,助理工程师,研究方向:信息安全。徐林杰,男,硕士,工程师,研究方向:信息安全。张祖平,男,硕士,工程师,研究方向:信息安全。李艳萍,女,工程师,研究方向:信息安全。
TP301.6DOI:10.3969/j.issn1672-9730.2014.05.012
