某轻型卡车驾驶室悬置振动试验分析与优化改进
2014-07-25朱学华戴云徐伟郭福祥
朱学华,戴云,徐伟,郭福祥
(1.南京汽车集团有限公司汽车工程研究院,江苏南京 210037;2.南京依维柯汽车有限公司,江苏南京 210028)
0 引言
随着我国商用车产业的快速发展,商用车的振动和噪声问题已日益凸显,乘员的乘坐舒适性已作为评价车辆性能优劣的一个重要指标,正越来越多地受到各大商用车厂家的重视。
轻型卡车驾驶室的悬置系统作为车架与驾驶室之间的弹性连接件,除了支撑驾驶室总成不与其他零部件发生干涉问题外,还有一项重要的功能是衰减来自动力总成、路面以及轮胎的激励经过车架向驾驶室传递的振动能量,从而减小驾驶室振动并提升乘坐舒适性。所以在新车型开发阶段,驾驶室悬置系统参数的合理设置对于隔振、减振以及使部件避开共振频率段将起到事半功倍的效果。
文中针对某轻型卡车在开发验证阶段暴露出的驾驶室在常用车速60 km/h左右车内振动过大问题,通过试验方法找出原因,进而提出驾驶室悬置系统优化匹配方案。优化后的主客观试验验证结果表明:该速度下车内的振动已大幅下降,提高了整车的NVH水平。
1 驾驶室系统的振动测试
1.1 确定试验测点位置
整车主观评价的结果显示在轻型卡车常用车速段60 km/h左右车内存在严重的低频共振问题。为了快速发现和解决问题,通过更换动力总成悬置、更换驾驶室悬置与加强支架等方式检查车内的振动水平,发现更换刚度变小的驾驶室悬置,车内的振动得到了较大程度减轻,而其他方式车内振动无明显变化,所以初步判定驾驶室悬置刚度不合理是引起驾驶室抖动问题的主要因素。为进一步弄清楚产生抖动问题的振动机制过程,项目组制定了详细的客观数据测试方案。考虑到车辆行驶时驾驶室除了受到动力总成工作激励外,还受到路面激励和轮胎不平衡引起的滚动激励的影响。依据振动信号的传递路径,测点分别布置在动力总成悬置的主被动端、驾驶员侧轴头、驾驶员侧车架、驾驶室悬置的主被动端、驾驶员座椅导轨以及驾驶室A柱等位置。测试设备包括比利时LMS公司的LMS Test.lab数据采集与分析系统、美国PCB公司的三向加速度传感器、发动机转速表、车速记录仪以及笔记本电脑等。
1.2 路面试验结果分析及对策
试验时采集车辆在平直的沥青路面上以合适挡位40~100 km/h车速 (10 km/h为速度间隔)匀速行驶以及以最高挡位从最低稳定车速匀加速到最高车速等试验工况下各测点的加速度响应信号,同时记录下发动机转速和行驶车速。
首先,对匀速工况下各测点的振动量随车速变化进行分析,得出的变化曲线如图1所示。由图1得出:最能反映驾驶室振动情况的A柱测点在60 km/h速度下的振动最为明显,振动幅值也最大,这与主观感受是完全一致的,这可能与在这个速度下驾驶室发生低频共振有关。再对A柱振动信号进行频谱分析得出振动最大的频率发生在7 Hz左右,如图2所示。
其次,为了寻找驾驶室振动过大的原因,对匀加速工况下各测点的阶次跟踪图进行分析,驾驶室A柱的阶次跟踪图如图3所示。由图3得出:驾驶室A柱振动受发动机的0.24阶振动影响最大,最大值发生在发动机转速约1 830 r/min、车速62 km/h左右以及频率7.3 Hz附近的区域内。通过理论计算,排除发动机激励的影响,再利用轮胎的滚动频率计算方法得到发动机0.24阶与轮胎1阶滚动频率相接近,这也就说明驾驶室的振动主要是由轮胎的滚动激励引起的。
再者,为确认轮胎振动激励到驾驶室的传递路径,需要对匀加速工况下驾驶室悬置振动信号做0.24阶的切片分析,如图4所示。由图4得出:驾驶室A柱的振动趋势与轴头振动趋势一致,且振动能量主要通过驾驶室前悬置传递到车内,说明该车速下驾驶室前悬置未起到良好的隔振效果。
1.3 驾驶室悬置系统模态测试分析
由于车速60 km/h时轮胎的滚动频率在7 Hz附近,该频率极有可能与驾驶室悬置系统的固有频率过于接近,从而产生频率耦合引起驾驶室共振问题,因此有必要对驾驶室总成系统进行模态测试分析,以获取其刚体模态参数。为了节约时间更快速地诊断出问题,同时避免考虑有限元仿真计算时复杂的边界条件,采用试验模态分析方法获取驾驶室悬置系统固有频率。文中运用LMS Test.lab Impact Testing模块进行模态参数识别,结果得到驾驶室俯仰运动刚体模态振型的固有频率为6.8 Hz,与车速60 km/h时轮胎的滚动频率7 Hz非常接近。
通过路面测试和室内模态测试结果可以判定:车速60 km/h左右驾驶室悬置对轮胎滚动激励隔振效果较差,同时轮胎滚动频率与驾驶室悬置系统固有频率相耦合,从而引起共振问题,加剧了驾驶室的抖动程度,因此有必要对驾驶室悬置作进一步的优化改进。
2 驾驶室悬置系统的优化匹配设计
2.1 获取驾驶室质心和转动惯量
运用LMS Test.lab Rigid Modal软件模块根据测得的频响函数计算出驾驶室的刚体模态,再由刚体模态参数可快速计算出驾驶室的质心和惯性参数。首先将驾驶室置于空气弹簧上模拟自由—自由的边界条件,再在驾驶室上均匀布置加速度响应测点,同时选择在驾驶室刚度较大位置作为锤击输入点,获取不同测点的频响函数曲线,试验系统支承方式如图5所示。这种刚体惯性参数的识别方法能大大简化以往识别方法的复杂性,有利于进一步提高识别效率和识别结果的准确性。表1为驾驶室总成的质心及惯性参数测试识别结果。
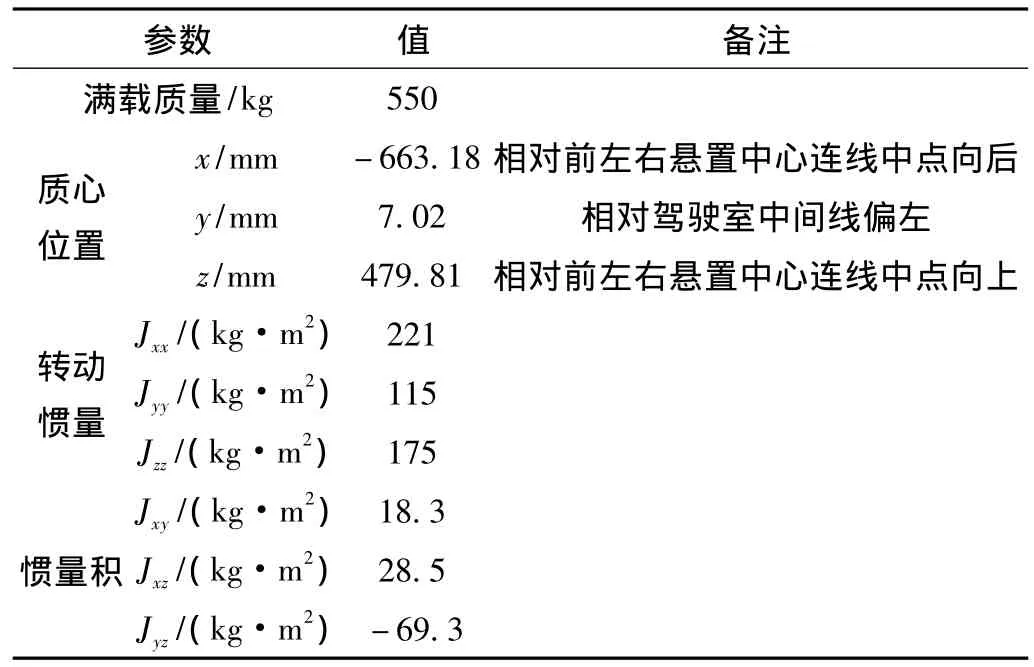
表1 驾驶室质心及惯性参数
2.2 建立驾驶室悬置系统的动力学模型
该样车驾驶室悬置的布置方式为四点支承,同时为进一步研究方便,可以把驾驶室悬置系统简化为有6个自由度的振动系统,具体可用驾驶室质心的3个直角坐标x、y、z,以及绕过质心平行于定坐标轴的3个坐标轴转角θx、θy、θz来表示。坐标方向定义为:在驾驶室总成静止时,原点与驾驶室总成质心重合,x轴指向驾驶室前方;y轴指向驾驶室左侧;而z轴指向驾驶室上方。简化后驾驶室悬置系统的动力学模型可用图6表示。通常悬置系统的模态解耦和优化设计是以系统各个模态下的频率和振型为理论基础。所以文中首先利用拉格朗日动力学方法建立驾驶室悬置系统的振动微分方程:
由于驾驶室的悬置系统采用普通的橡胶悬置弹垫,阻尼一般很小,且系统的固有振动频率与阻尼无关,所以在作系统模态分析时可不予考虑,可认为C=0;此时振动方程可以改写成:
式 (2)— (4)中:M和K分别是悬置系统的质量矩阵和刚度矩阵;Ei为悬置系统的悬置点坐标位置组成的矩阵;Bi为悬置的安装方向角余弦值组成的矩阵;Di为悬置三向刚度组成的矩阵;x是刚体的广义坐标矢量。在通过相关试验方法获取驾驶室的质量、质心位置、转动惯量、转动惯量积、悬置点坐标、悬置安装角以及橡胶悬置x、y、z三个轴方向刚度参数的基础上,再利用系统的动能、势能和广义坐标矢量之间的关系式可得到质量矩阵M和刚度矩阵K的表达式。再将式 (2)转换到频域内,可得到:
对式 (5)作模态分析,即可得到驾驶室悬置系统6个自由度的模态频率fi(i=1,2,…,6)和相应振型 φi=[φ1i,φ2i,φ3i,φ4i,φ5i,φ6i]T。
2.3 驾驶室悬置系统固有频率的设置
为避免发生共振问题,悬置系统固有频率的设置应满足以下2点要求:(1)各阶次的固有频率应相互错开;(2)各阶次固有频率还应该避开悬架偏频、车架模态频率以及发动机怠速激励频率。
2.4 驾驶室悬置系统的振动能量解耦
系统解耦可使系统各个自由度方向上振动相对独立,避免发生2个或多个耦合振动的模态产生互相激励,导致振动响应放大的现象。悬置系统的振动解耦关键是控制好系统6个自由度上的固有频率分布,且沿各自由度方向的振动是解耦的。由于目前有关悬置系统匹配大多采用能量解耦法,因此文中也将以驾驶室悬置系统的振动解耦问题视为首要的目标函数进行优化改进。
依据上述驾驶室悬置系统的动力学模型,当悬置系统以第i阶固有频率fi和振型φi振动时,第n(n=1,2,…,6)个广义坐标上分配到的动能所占悬置系统总动能的百分比为:
式中:mnl为质量矩阵M的第n行、第l列元素;φni是φi第n个分量;φli是φi第l个分量。E(n,i)表示系统在第i阶固有频率振动时,振动占优方向所占的振动能量的百分比。此数值越大表示系统的解耦程度越高。
2.5 驾驶室悬置系统的设计变量
由于该样车驾驶室的前期设计数据已全部冻结,因此通过更换驾驶室总成、改变悬置的安装位置和角度等措施来改善振动耦合的方式减小振动传递存在较大的实施难度。结合驾驶室悬置系统动力学模型,并综合考虑到样车的实际情况,利用改变悬置本身的特性方法来降低系统的振动,相比而言较容易实施。而悬置系统阻尼特性的主要作用是降低共振峰幅值,对系统的解耦作用影响很小,因此文中选取各悬置各向主轴刚度作为设计变量。
2.6 悬置系统的优化计算及结果
将以悬置系统动力学模型为理论依据,并以悬置系统的解耦度为目标函数,悬置系统固有频率分布的设置以及悬置刚度上、下限值为约束条件,悬置系统的刚度作为设计变量,同时结合驾驶室和悬置参数测量结果进行综合优化计算。因此,文中采用矩阵计算功能强大的MATLAB软件编制程序来计算和优化系统的固有频率和解耦率。在综合考虑驾驶室悬置系统的固有频率分布、振动能量的解耦率、驾驶室静平衡姿态以及疲劳可靠性等因素,最终悬置优化后结果如表2所示。表2反映了优化后前悬置的x和y向刚度未变化,而后悬置的x向刚度提高,y向刚度降低,同时z向刚度均有所降低。此外,表3和4既说明了相比于原车状态优化后悬置系统的固有频率分布更合理,驾驶室振动能量解耦率明显提高;另一方面也再次验证了车速60 km/h左右车内共振问题是由于原悬置系统振动能量解耦度不高以及轮胎滚动频率与驾驶室悬置系统固有频率相耦合共同导致的。
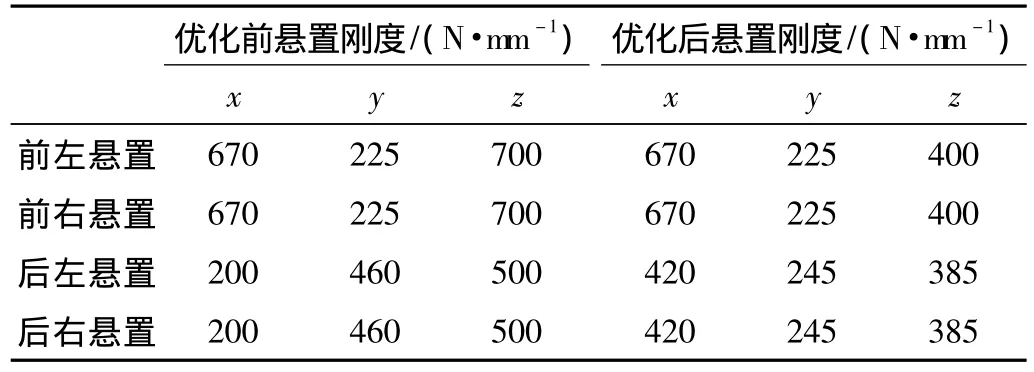
表2 优化前、后悬置刚度值变化

表3 优化前悬置系统的固有频率和解耦率
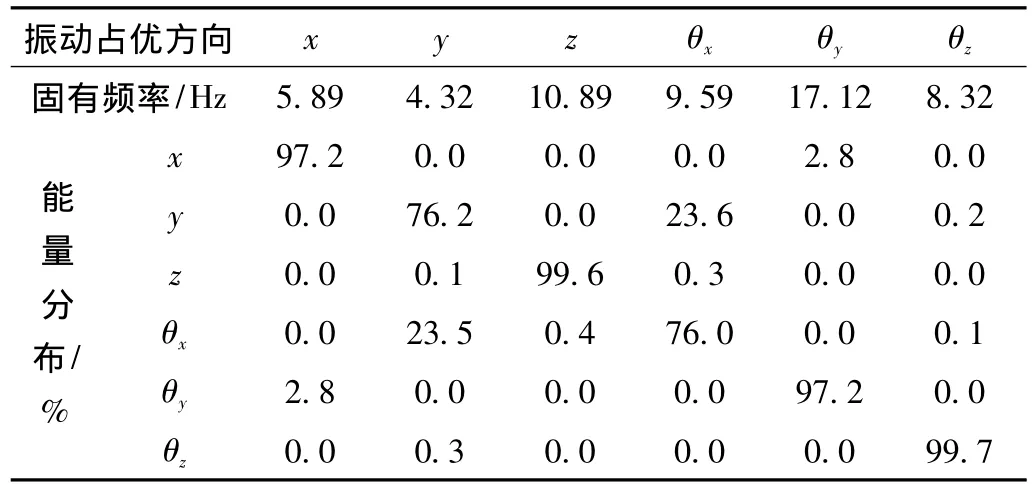
表4 优化后悬置系统的固有频率和解耦率
3 优化后驾驶室悬置系统试验验证
根据驾驶室悬置优化改进的计算结果,委托供应商重新试制了样件,并将其安装在原车上进行试验验证。主观评价车速60 km/h左右车内严重的抖动问题已基本消除,客观数据也验证了该车速下驾驶室A柱振动已大幅减小,如图7所示。总之,驾驶室悬置的重新匹配优化对驾驶室振动起到了显著改善作用,达到了改进的目的。
4 结论
针对主观评价车速60 km/h左右车内存在严重的抖动问题,从测点布置、试验工况等方面详细叙述了试验过程并深入解读了试验数据。依据振动信号的传递路径分析发现轮胎滚动频率与驾驶室悬置系统固有频率发生耦合以及前悬置隔振效果不佳等因素共同造成了车内较大振动,严重影响了车内舒适性。针对此问题,获取了驾驶室质心和惯性参数,建立了悬置系统多自由度的动力学模型,依据悬置系统固有频率合理分布和振动能量解耦为匹配设计理论,并以悬置刚度为设计变量,运用MATLAB软件编制程序对驾驶室悬置系统重新进行优化匹配。优化后样件装车试验结果表明:车内振动已明显减小,达到了改进的目的。
总之,文中详细叙述的有关驾驶室悬置振动试验与数据分析方法以及优化匹配方法对今后悬置开发具有重要的借鉴意义。
【1】Zhang Han,Guo Xuexun,Fang Zhigang.Application of Wavelet A-nalysis in Truck Cab Vibration Signal Processing[R].SAE Paper,2012-01-2011.
【2】Jeong T,Singh R.Analytical Methods of Decoupling the Automotive Engine Torque Roll Axis[J].Journal of Sound and Vibration,2000,234(1):85-114.
【3】庞剑,谌刚,何华.汽车噪声与振动一理论与应用[M].北京:北京理工大学出版社,2006.
【4】杨雷,黄鼎友,王鑫蜂,等.MATLAB在动力总成悬置系统优化设计的应用[J].机械设计与制造,2011(5):93-95.
【5】王天利,孙营,田永义.基于能量解耦的汽车动力总成悬置系统优化[J].机械设计与制造,2006(7):31-33.
【6】付江华,史文库,沈志宏,等.基于遗传算法的动力总成悬置系统优化研究[J].振动与冲击,2010,29(10):187-190.
