斜拉索张力优化研究

朱 敏, 李衍赫

(1.中铁工程设计咨询集团有限公司，北京 100055;2.浙江大学 建筑工程学院,浙江 杭州 310058)

斜拉索张力优化研究

朱 敏1, 李衍赫2

(1.中铁工程设计咨询集团有限公司，北京 100055;2.浙江大学 建筑工程学院,浙江 杭州 310058)

合理确定斜拉索的预张力是斜拉空间网格结构成败的关键，提出一种适用于半刚性结构的静力平衡法线性迭代优化方法。通过对灵武体育中心体育场屋盖斜拉索张力优化分析，获得{N3}=(1+0.3)N为优化预张力，结构最大竖向位移为跨度的1/718，各杆件应力/强度比基本在0.8以内。

体育场屋盖;斜拉索;预张力;优化

0 引言

体育场等大型斜拉空间网格结构体系，多为拉索与空间桁架、塔柱组成的刚柔组合体系。通过悬挂在塔柱顶部的拉索拉吊桁架网格结构，并利用拉索的预张力，形成桁架网格的中间弹性吊点，使空间网格结构内力和变形得以调整，减小结构的绝对跨度，降低桁架杆件的内力和变形[1]。

在斜拉网格结构中，一般增加拉索的预张力，部分抵消结构的外荷载作用，桁架网格结构杆件内力降低、挠度减小；塔柱结构的柱顶位移和塔体结构的内力加大[2-4]。拉索的预张力过大，钢筋混凝土材料的塔柱(又称巨柱)则需承担过大的偏心应力，虽然混凝土塔柱多采用预应力混凝土来解决偏心应力，这也可能导致塔柱设计不合理。因此，合理的拉索预张力是改善结构性能、提高综合经济效益的重要技术措施，使空间钢结构体系获得良好结构性能和经济指标的有效方法。在确定拉索预张力时要综合考虑杆件内力、结构挠度、塔柱结构位移与内力等因素，同时须保证在温度应力、风吸力等影响下拉索正常工作。

在确定拉索的初始张力时，常用的方法有倒退分析法和前进分析法[5]、基于初始应变影响矩阵法和多次复形法等，这些方法的缺点是操作复杂。因此，结合实际工程，提出一种基于变形控制的静力平衡法的线性迭代优化方法。

1 灵武体育中心体育场工程概况

位于灵武市新区行政中心的灵武体育中心[1]体育场，距银川市38 km。体育中心由25 401座的体育场和约3 000座体育馆、服务系统与配套设施等构成。其中，体育场底部面积36 521 m2，总建筑面积27 173 m2。东、西区看台固定座席25 401个。椭圆型屋盖的长轴跨度214 m、短轴跨度193.7 m。体育场挑棚高38.76 m、挑棚长40 m，拉索吊点前的悬背长13.16 m。

体育场屋盖由斜拉桁架、拉索、斜塔柱构成受力体系。沿体育场环向共有84根塔柱(又称巨柱)，每根巨柱引出1根径向索和2根斜向拉索，吊挂着空间桁架。屋盖挑篷桁架为弧形曲面，前高后低。沿巨柱的椭圆方向为径向主桁架，截面为3根钢管构成的空间倒三角型(V型)，根部截面高度约为2.0 m，端部截面高度约为1.4 m，宽度1.5 m。主桁架前部1/3处通过拉索与外斜巨柱的上端连接。各榀径向桁架之间有环向桁架，其中中间环向桁架布置在钢索位置，端部布有提拉桁架和封边桁架，以增加屋盖结构的整体性。

斜拉钢索为耐腐性好的半平行钢丝束，规格根据长度分别为Φ5×61和Φ5×121，对应钢丝束直径分别为45 mm和61 mm，截面面积分别为1 198 mm2和2 376 mm2。

2 相关计算参数及主要计算荷载

2.1 计算参数

钢材的弹性模量2.06×105N/mm2、泊松比0.3、容重7 850 kg/m3，钢材线膨胀系数取(计算温度荷载时)1.2×10-5m/m℃。抗拉、抗压和抗弯强度设计值为250 N/mm2。

拉索钢丝束弹性模量1.95×105N/mm2、泊松比0.3、容重7 698 kg/m3，抗拉强度标准值为1 670 MPa，抗拉强度设计值取930 MPa。两种规格的钢丝束破断力分别为2 000 kN和3 968 kN；为保证结构的安全度，在各工况下拉索实际设计拉力应小于0.4Nb(分别为500 kN和1 587 kN)。

2.2 计算荷载

(1)钢结构自重G。考虑钢节点、加劲肋等增加的自重，计算中按钢材容重取1.1倍的放大系数。

(2)屋面活荷载L。膜屋面、檩条、雨水管道、照明设备等，按0.5 kN/m2取值。

(3)基本雪压S0。50 a按0.20 kN/m2，100 a按0.25 kN/m2。

(4)合龙温度T。 10±5 ℃，根据当地气象资料，设计最大正温差取+35 ℃，最大负温差取-25 ℃。

(5)风荷载WL。按照风洞实验的结果，不同部位的上吸风压值为-2.48～1.2 kN/m2。

3 拉索预张力静力平衡法线性迭代优化计算方法

3.1 静力平衡法计算原理

基于变形控制的静力平衡法过程如下：

(1)首先不施加预张力，即在屋面荷载和结构自重作用下求得各索的内力，求得的各索内力记作{N}。

(2)调整预张力,以1+i{N}(i=0.1,0.2,…)进行迭代计算，使结构的整体变形控制在跨度的1/1 500以内。

(3)考虑屋盖的受风吸力，还需保证结构在最不利吸风荷载作用载下拉索不松弛。

3.2 基于静力平衡法线性迭代优化方法

3.2.1 目标函数的选取

根据灵武体育中心体育场工程的特点，目标函数选取杆件应力/强度比，表达式为

(1)

式中,λi为各杆件的截面编号；Ni为各杆件最不利组合下的内力值；Ai为各杆件的截面面积；fi为各杆件材料强度设计值。

3.2.2 优化线性插值函数的选取

由于目标函数唯一，杆件应力/强度比的优化属一维优化问题。一维优化方法第一类为试探法，第二类为线性搜索法。其中线性搜索法根据是否采用导数信息分有导数和无导数方法，无导数方法的搜索方法有直接插入法、0.618法、Fibonacci法等。

线性搜索是多变量函数最优化方法的基础，在多变量函数优化中，迭代格式为

(2)

式中,∂k为步长因子;dk为搜索方向。设

(3)

从xk出发，沿搜索方向dk，确定步长因子∂k，使

(4)

3.2.3 优化方法

第一阶段从{N1} =N到第六{N6}，Ni=N1+(I-1)N，I=1,2,…,6。

第二阶段在第一阶段数值接好的Ni值范围内按式(5)进行分析

(5)

第三阶段在第二阶段数值接好的Ni值范围内再次线性插值分析。理论上讲，阶段次数越多，优化结果更好，但一般2～3次可满足设计精度要求。

选取不同预张力批次对结构进行反复计算，最终找出使得杆件应力/强度比和结构竖向位移最小的批次即为最优初始预张力。

4 灵武体育场斜拉屋盖拉索预张力优化计算分析

采用上述的基于变形控制的静力平衡法计算灵武体育场斜拉屋盖拉索预张力，借助Midas/gen有限元设计软件进行求解。

4.1 基本假设

未计入拉索初始缺陷,为了便于求解且满足工程简化精度要求，模拟中将巨柱简化为拉索的固定支座。斜拉网格结构中，增加拉索的预张力，桁架网格结构杆件内力降低、挠度减小；但塔柱结构的柱顶位移和塔体结构的内力加大。依据斜拉网格结构的计算结果，再分析巨柱钢筋混凝土应力和优化混凝土巨柱钢筋预应力值。再通过检验和校正屋盖拉索与张力。

4.2 计算模型

采用Midas/gen有限元计算程序，以西侧屋盖为对象建立有限元模型。桁架中的弦杆和腹杆采用桁架单元，拉索采用索单元，计算模型如图1所示。各拉索的编号及对应位置如图2、表1所示。

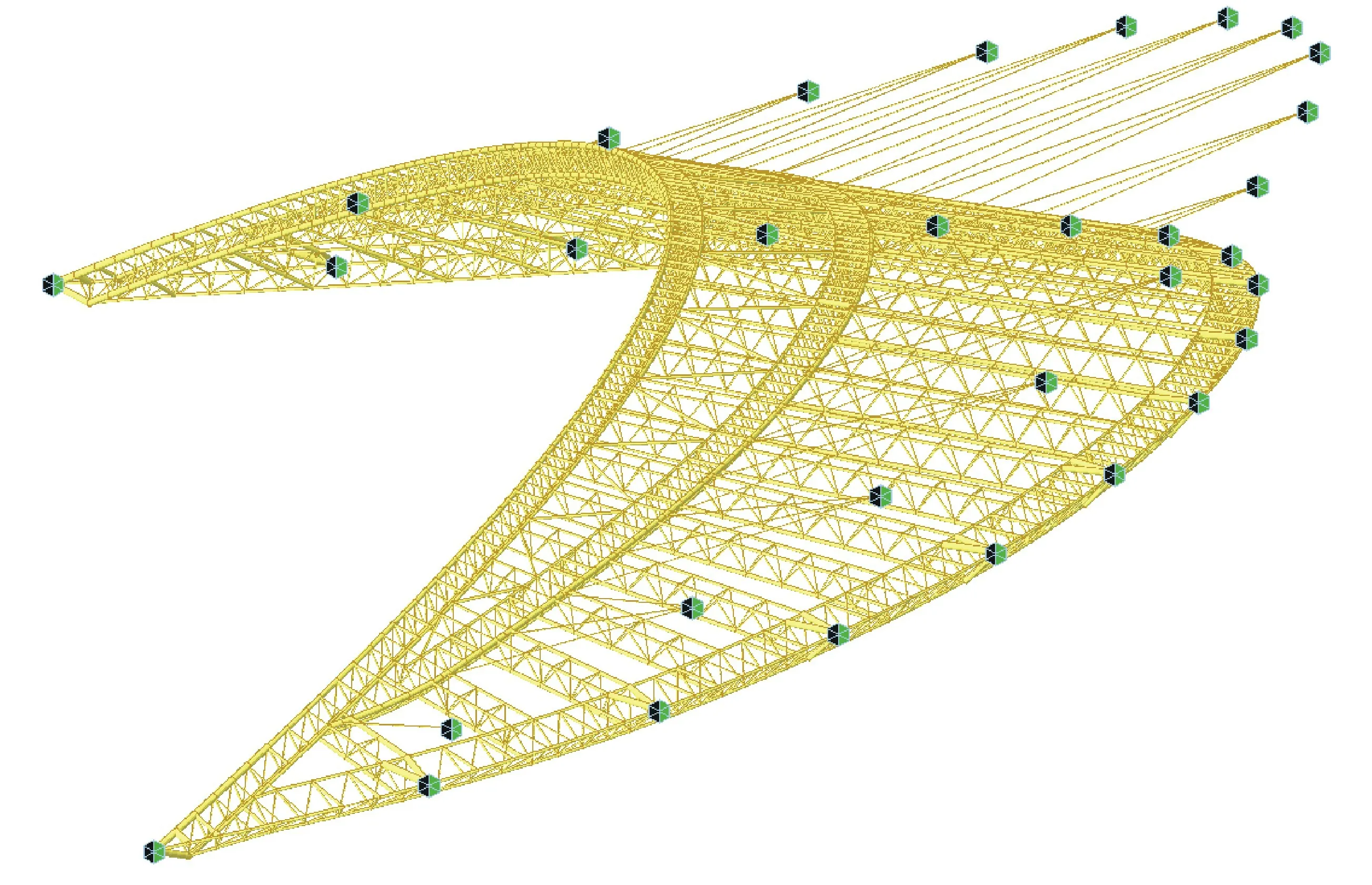
图1 有限元网格计算模型

图2 拉索分布位置示意

由于结构为左右完全对称形式，故图2只示意了右侧一半的拉索布置情况，另外左侧一半拉索的布置情况与此完全对称。

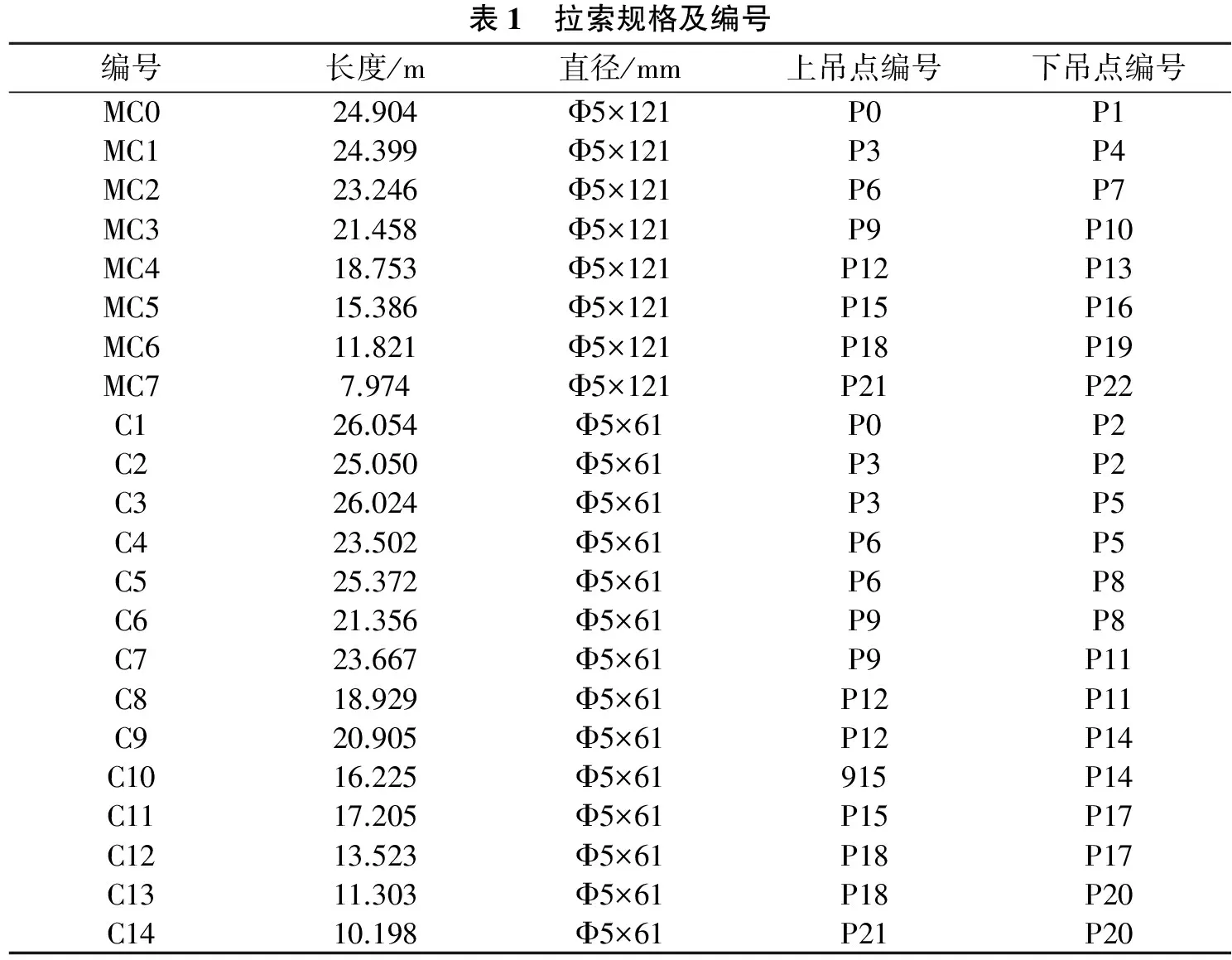
表1 拉索规格及编号编号长度/m直径/mm上吊点编号下吊点编号MC024．904Φ5×121P0P1MC124．399Φ5×121P3P4MC223．246Φ5×121P6P7MC321．458Φ5×121P9P10MC418．753Φ5×121P12P13MC515．386Φ5×121P15P16MC611．821Φ5×121P18P19MC77．974Φ5×121P21P22C126．054Φ5×61P0P2C225．050Φ5×61P3P2C326．024Φ5×61P3P5C423．502Φ5×61P6P5C525．372Φ5×61P6P8C621．356Φ5×61P9P8C723．667Φ5×61P9P11C818．929Φ5×61P12P11C920．905Φ5×61P12P14C1016．225Φ5×61915P14C1117．205Φ5×61P15P17C1213．523Φ5×61P18P17C1311．303Φ5×61P18P20C1410．198Φ5×61P21P20

第一阶段首先计算{N1}=1.0{N}({N}为屋面恒载，拉索预张力为0.0)，并分别计算{N2}=1.1{N}～{N6}=1.6{N}。因{N7}对应的结构最大竖向位移大于71 mm，超过跨度的1/1 500。{N1}工况的计算结果如表2和表3所示，其它工况计算结果见图3～图5。

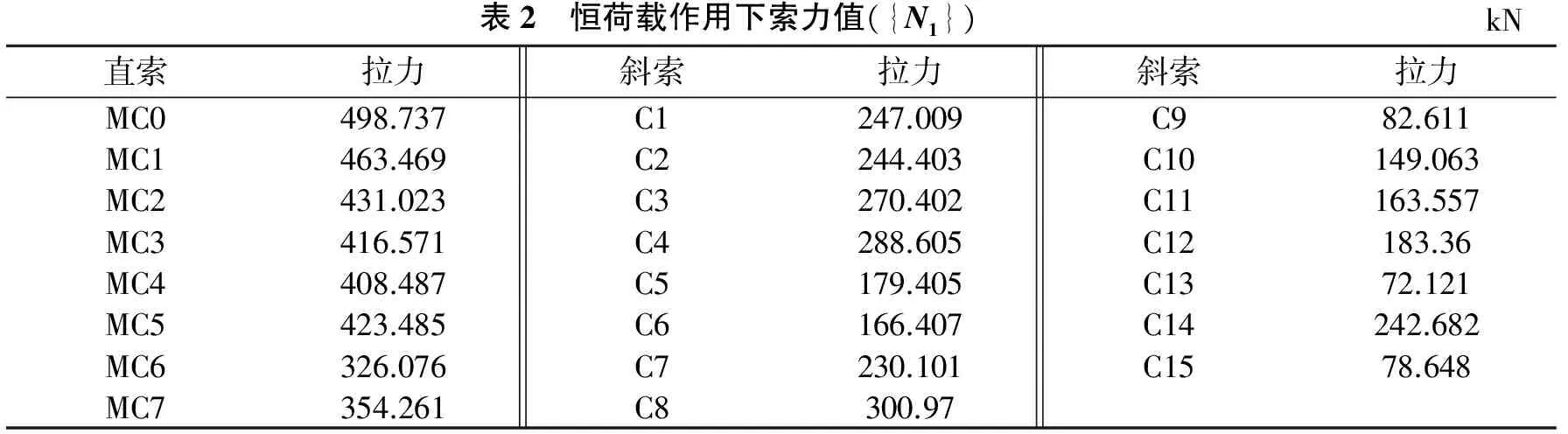
表2 恒荷载作用下索力值({N1})kN直索拉力斜索拉力斜索拉力MC0498．737C1247．009C982．611MC1463．469C2244．403C10149．063MC2431．023C3270．402C11163．557MC3416．571C4288．605C12183．36MC4408．487C5179．405C1372．121MC5423．485C6166．407C14242．682MC6326．076C7230．101C1578．648MC7354．261C8300．97

表3 恒荷载和{N1}作用下下结构竖向位移值(向下为正)mm工况索拉点桁架端点桁架跨中杆件最大应力/强度比恒+预张力-5-8-40．95最大包络412532304

第二阶段可根据第一阶段计算结果，缩小搜索范围、即在小范围内插值优化。本文根据第一阶段拉索预张力线性分布特征，第二阶段仍然在全部范围内插值计算。{N1}、{N1}+{N1-N2}/2、{N2}、{N2}+{N2-N3}/2、{N3}、…、{N6}的计算结果如表4和图3～图5所示。

由图3恒+预张力和图4最不利荷载组合时的桁架跨中竖向位移与拉索预张力关系可知，桁架跨中竖向位移与拉索预张力呈近似线性关系，拉索预张力越大、桁架跨中竖向位移越大。由图4可知，在{N6}预张力及最不利荷载组合作用时桁架跨中竖向位移变成向上的负位移(-12.8 mm)。由图5可知，最不利荷载组合作用时桁架杆件应力/强度比与拉索预张力关系呈“抛物线”型，拉索预张力较小时杆件应力/强度比先随拉索预张力增大而减小，拉索预张力较大时随拉索预张力增大而快速增加。根据杆件应力/强度比的优化目标，初步判断最优预张力在{N3}附近。

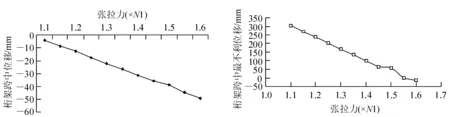
图3 不同拉索预张力及恒荷 图4 不同拉索预张力及最不利 载作用的桁架跨中竖向位移 荷载组合时下桁架跨中竖向位移

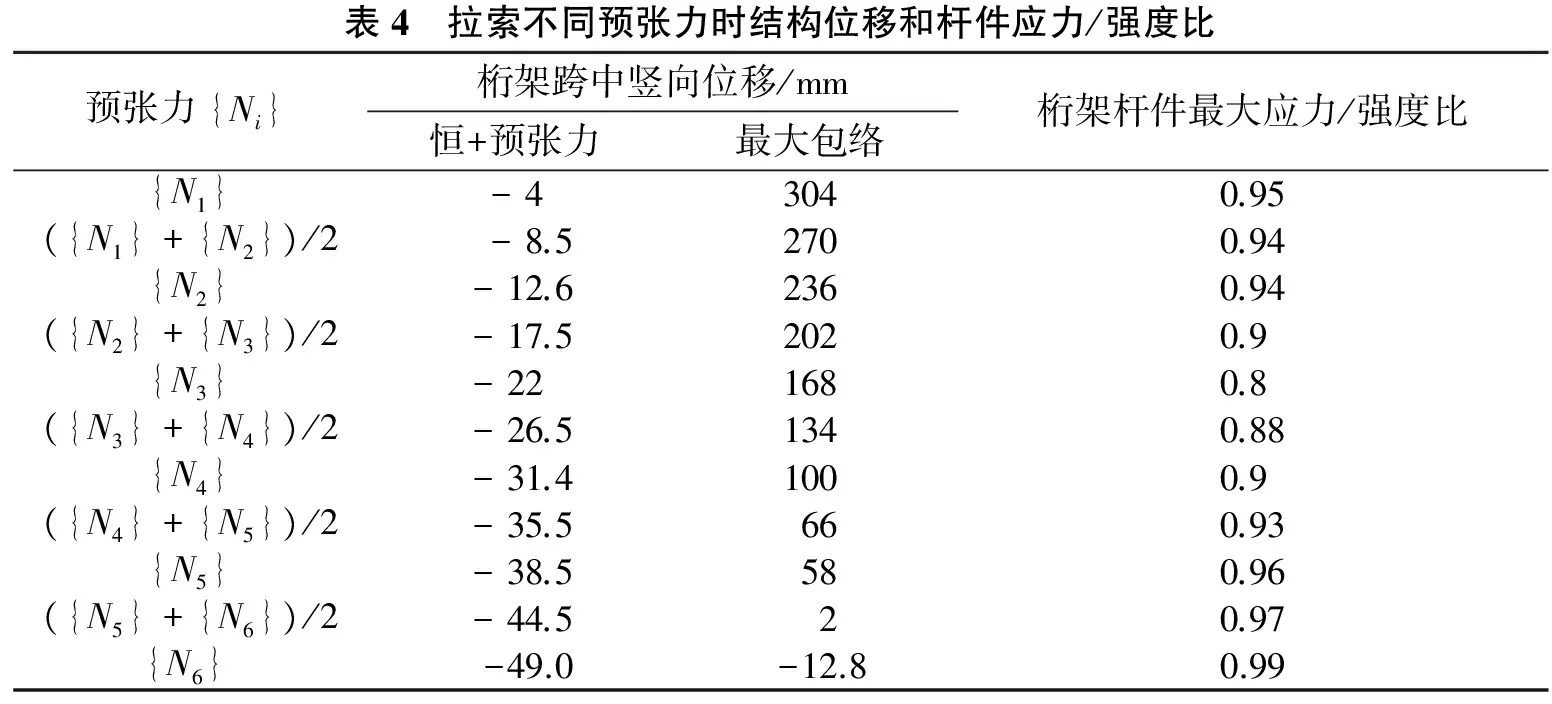
表4 拉索不同预张力时结构位移和杆件应力/强度比预张力{Ni}桁架跨中竖向位移/mm恒+预张力最大包络桁架杆件最大应力/强度比{N1}-43040．95({N1}+{N2})/2-8．52700．94{N2}-12．62360．94({N2}+{N3})/2-17．52020．9{N3}-221680．8({N3}+{N4})/2-26．51340．88{N4}-31．41000．9({N4}+{N5})/2-35．5660．93{N5}-38．5580．96({N5}+{N6})/2-44．520．97{N6}-49．0-12．80．99

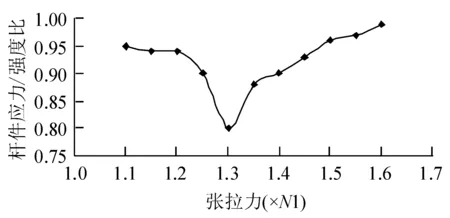
图5 不同拉索预张力及最不利荷载组合时桁架杆件应力/强度比

为进一步寻求优化的拉索预张力，在拉索预张力为{N3}邻近进行插值分析。在{N2}和{N3}间进行4分点插值：{N2}，{N2}+{N2-N3}/4，{N2}+{N2-N3}/2， {N2}+{N2-N3}/4，{N3}。4分点插值分析结果与2分点插值分析结果规律一致，并且仍然以拉索预张力为{N3}时杆件应力/强度比最小。

综合考虑结构位移和杆件应力/强度比，拉索预张力为{N3}是本工程的优化计算结果。

5 结论

(1)合理确定斜拉索的预张力是斜拉空间网格结构成败的关键，随着拉索预张力的加大、网格结构杆件内力峰值降低、挠度减小，但塔柱的柱顶位移、塔体附加弯矩加大。因此，提出一种适用于半刚性结构的基于变形控制的静力平衡法基础上的线性迭代优化方法。

(2)将不施加预张力、在屋面荷载和结构自重作用下求得各索的内力为拉索基本值，以N+0.10N的倍数进行一定拉力值计算，再在基本合理的拉力范围内线性插值计算，达到杆件强度/应力最小、结构变形在1/1 500的优化目标。

(3)通过对灵武体育中心体育场屋盖斜拉索张力优化分析，获得{N3}=(1+0.3)N为优化预张力，结构最大竖向位移与初始预张力(N)相比减小了近1/2，数值为跨度的1/718，各杆件应力/强度比基本均在0.8以内。

[1]朱敏.体育场柱索体系预应力优化研究[D].北京：北京交通大学土木学院，2013.

[2]董石麟.我国大跨度空间钢结构的发展与展望[J].空间结构,2000,6(2):3-13.

[3]姜正荣,王仕统,魏德敏.斜拉网格杂交结构设计中的若干问题[J].工程设计,2005,20(7):41-44.

[4]梁明,周岱,柳杰,等.斜拉空间网格结构的索系张拉和预应力控制[J].上海交通大学学报,2005, 39(5):769-773.

[5]冯健,张耀康.预应力斜拉网格结构的静力优化分析[J].东南大学学报:自然科学版,2003,33 (5):583-587.

(责任编辑 刘宪福)

Research on Optimization of Stay Cable Tension

Zhu min1, Li Yanhe2

(1.China Railway Engineering Consulting Group Co., Ltd, Beijing 100055, China;2.Institute of Structural Engineering, Zhejiang Unverisity, Hangzhou310058,China)

Reasonable determination of the pre-tension in cables is the key point to the success of cable-stayed spatial grid structure. This paper presents a linear iterative optimization method of static equilibrium method suitable for semi-rigid structure. By analyzing and optimizing the tension in the roof cables of Lingwu Sports Center Stadium, this paper obtains the conclusion that {N3}=(1+0.3)Nis the optimized pretension of the cables, and under this circumstance, the maximum vertical displacement of the structure is 1/718 of the span and the stress / strength of each rod is less than 0.8.

stadium roof; cable-stayed; pretension; optimization

10.13319/j.cnki.sjztddxxbzrb.2014.03.03

2014-05-04

朱敏 女 1988年出生 实习工程师

U448

A

2095-0373(2014)03-0012-06