基于CHC算法的集卡与岸桥协调调度优化问题

韩晓龙，牟少莉

(上海海事大学物流研究中心，上海201306)

1 文献综述

集装箱码头运输已经发展成为全球国际贸易中最重要的运输方式之一。近年来，随着集装箱码头的扩建、集装箱数量的增加、作业设备调度规则的不断更新，以及码头设备资源管理的复杂性，使得码头集装箱调度逐渐成为一项非常复杂的工程。研究者对集装箱码头作业设备的调度优化研究层出不穷。BISH等［1－2］提出了一个车辆位置分配问题，堆场龙门吊的位置已知，因此，在卸载集装箱时，有优先约束以及在多台龙门吊和多辆集卡的情况下，对装、卸集装箱同时作业问题进行了优化。文献［3］基于码头堆场堆存能力，建立了集卡分派优化两阶段模型，分别用Lingo和Gurobi进行求解，得到最优方案。NISHIMURA等［4］将一定数量的集卡分配给岸桥进行作业，在岸桥位置已知时，建立单车和多车两种情况下的模型，并用遗传算法对相应问题进行求解。张莉等［5］分析了集卡的数量配置对集装箱码头装卸作业的影响，并使用Witness仿真软件，得出在装卸不同时段进行动态调配，集卡车速提高并不一定能加快整船的装卸效率。曾庆成等［6］研究了集卡调度问题，建立集卡调度动态模型，使岸桥装卸作业时等待时间最小。随着集卡数量的增加，通过Q学习算法求解结果优于最长等待时间、最远距离等调度策略，以及动态分配集卡要优于静态分配集卡的策略。KOO等［7］提出了一种基于启发式禁忌搜索算法的新型车队管理程序，运用网络流的方法建立以车辆的空载时间最小为目标的模型，使用禁忌搜索算法优化车队大小并求出运输路径。张波等［8］将模拟退火算法应用于路径优化问题中，对类似货郎担的车辆路径问题进行求解，并用该算法得到最优计算结果与树形算法进行比较，克服传统优化算法局部求解的缺点，在解决城市道路交通方面的问题中具有一定的实用价值。CAO等［9］研究的是岸桥与集卡的综合调度，在进行卸箱作业中，建立以总完工时间最小为目标的MIP模型，运用遗传算法以及基于Johnson规则的改进启发式算法求解模型，得到协调调度方案的最优解。CAO等［10］研究集卡与龙门吊的协调调度(i－YTYCSP)，建立了一个整数规划模型，用通用 Benders分解方法和组合Benders分解方法来求解模型。WOOYEON等［11］研究交叉对接系统，可以预测集卡在码头的卸箱作业以及如何分配集卡，从而找到较好的集卡调度序列，以减少总作业时间，提高码头作业效率，其采用启发式算法对临时存储交叉对接问题进行求解。EBRU等［12］研究集装箱码头同时进行装卸作业，对作业集卡进行合理调度，减少作业总时间，并考虑到绝对和渐近情况，运用启发式算法进行求解，通过数值实验，取得该调度问题的最优结果。

然而，在文献中，对码头作业设备协同调度问题研究较少，未考虑实际操作的约束及模型求解的复杂性，故笔者考虑岸桥与集卡在实际作业中的绝对重要性以及约束，建立岸桥与集卡的协同调度优化模型，用改进的遗传算法(CHC算法)进行求解，提高求解准确性，实现集卡的最优调度。

2 问题描述及数学模型构建

2.1 问题描述

在港口实际操作中，为船舶配置一定数量的岸桥和集卡，集装箱作业可以看成码头内部的水平运输物流系统，主要包括装、卸两个流程，集卡则是该流程中的主要运输设备，是连接岸桥与堆场的中间设备，笔者基于一定的实际作业条件约束，研究岸桥与集卡的协同调度问题，在集装箱进口作业中，集卡完成一次作业后，空载返回岸桥，等待进行下一次作业，如此反复，最小化集卡的最大完工时间。集卡的一个简单作业循环流程如图1所示。

图1 集卡作业循环流程

2.2 模型基本假设

为了便于求解，对问题进行一定的简化。根据港口集卡的卸船作业实际情况提出如下假设:

(1)只考虑码头船舶卸箱作业;

(2)不同的岸桥提取集装箱时间点不同，但每次作业时间均相等;

(3)集卡一次只能运输一个集装箱;

(4)岸桥间互不存在约束，不能对同一集装箱重复操作，不存在等待集卡的情况;

(5)龙门吊互不存在约束，数量足够对集卡的作业，无需等待。

2.3 模型参数设置

笔者将每个待作业的集装箱视为一项作业，序号为 i，j，共有 Q 项作业，k 辆集卡，k，l分别为集卡的作业序号，N台岸桥，m，n分别为岸桥的作业序号。此外，定义两个虚拟工作0和n+1，分别表示集装箱的初始和最终作业状态。该模型采用的参数如下:

N为岸桥的作业数量;K为集卡的作业数量;Q为集装箱的作业数量;ukilj为岸桥在集卡k作业i后立即对集卡l作业j的准备时间;p为岸桥m对集卡k上作业i的作业时间;ukij为集卡k作业i后立即作业j的准备时间;t为集卡进行作业的运输时间;r为龙门吊从集卡卸箱的作业时间;M为一个很大的数;Smi为岸桥m进行作业的开始时间;cmi为岸桥m进行作业的完成时间;Ski为集卡k进行作业的开始时间;cki为集卡k进行作业的完成时间。

模型中决策变量如下:

2.4 构建数学模型

目标函数即最小化作业总完工时间为:

式(1)为目标函数，求总完工时间最小;式(2)为最后总完工时间，由最后一辆集卡作业完成时间决定;式(3)和式(4)为对岸桥作业先后顺序的约束;式(5)为岸桥m对集卡l作业j开始时间的约束;式(6)为岸桥m对集卡l作业j的完成时间约束;式(7)为岸桥作业结束后集卡再开始作业;式(8)和式(9)为同一辆集卡作业的先后顺序约束;式(10)为对集卡 i后序作业j的顺序约束;式(11)为集卡一次作业的时间约束;式(12)为不同集卡作业先后顺序;式(13)为集卡一次只能进行一次作业;式(14)为作业先后顺序约束。

3 模型求解

3.1 CHC算法应用

遗传算法计算简易流程如图2所示。

图2 遗传算法计算简易流程图

笔者以2台岸桥，4辆集卡和12只集装箱作业为例，根据集卡调度的规则，结合CHC算法，进行求解。

3.1.1 编码

CHC采用整数编码，随机生成12个1和N(N为岸桥的数量)的随机数作为岸桥对集装箱的作业序号，如图3所示。

图3 岸桥作业集装箱作业序号

同时可得岸桥与集卡作业的初始种群，如表1和表2所示。

表1 岸桥(QC)初始分配任务

表2 集卡(YT)初始作业分配任务

3.1.2 适应度计算

遗传算法中适应度函数与目标函数有较大的关联，笔者采用界限构造法，若优化问题为求最小值问题，则 fit(f(x))={cmax－f(x)，f(x) ＜cmax};若优化问题为求最大值问题，则 fit(f(x))={f(x)－cmin，f(x) ＞cmin};其中，f(x)为求解问题的目标函数，cmax为f(x)最大值估计，cmin为 f(x)最小值估计。

笔者求解的目标函数为集卡总完工时间最小值问题，定义f(x)为目标函数，即f(x)=min T，那么，适应度函数可表示为:fit(f(x))=c－f(x);c取值为200，即 fit(f(x))=200－T。

3.1.3 选择

笔者使用跨世纪精英的最佳保留选择法，使用轮盘赌选择后，将当前种群中适应度最高的个体结构完整地复制到子代，保留适应度较高的个体，不会因为选择操作的误差而被淘汰掉，提高精确度，选取11个个体的适应度，选择概率，累计概率，如表3所示。

表3 CHC算法的跨世纪精英选择法

假设抽取随机数0.79，介于第5和第6个个体之间，那么第6个个体被选中，以此类推，选取最佳个体。

3.1.4 交叉

改进的CHC算法使用两点交叉，随机地产生两个实数 k，h(1≤k≤h≤N) ，取 k=2，h=10，从而确定交叉点位置，N为染色体长度，取N=12，选取交叉点之间的部分染色体交叉，图示如图4。

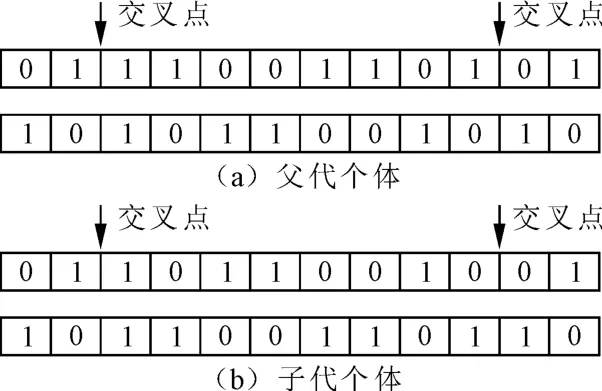
图4 两点交叉

3.1.5 变异

笔者采用基本位变异法，对某一个体，通过已确定或动态确定的变异概率确定是否对其进行变异;再随机产生一个变异点k(1≤k≤W－1)，取k=1，W为个体中变异点的数量，取W=1，最终确定一个变异点，用等位基因替代产生新子代。

3.2 参数设定

遗传算法自身参数有种群大小n、迭代代数gen、交叉概率pc和变异概率pm。种群大小n的取值范围一般取为20～100，本着种群规模不宜太大，取n=50。进化代数应结合染色体长度和种群规模等因素进行综合考虑，取进化代数gen=100。研究问题染色体长度取为N=12，在实际操作中，作业规模会变得很大，染色体长度也会相应增加。

进化终止的条件规定:在种群中最大适应度值已趋于稳定、增加不超过0.5%，或平均适应度值相对稳定、增加不超过3% 的时候，可以终止遗传算法，取进化代数到达规定值终止运行。

交叉采用两点交叉方式，交叉概率pc=0.8，变异采用基本位变异方法，如图5所示，已进行交叉的个体不再参与变异，这里变异概率 pm=0.05，变异概率为 pm/(1－pc) 。

图5 基本位变异

3.3 算例结果及分析

将遗传算法在Matlab 7.12(R2011a)软件，MicrosoftWindows 7系统环境下实现，得到基于集卡总完工时间最小，桥吊最优任务序列及作业时间、集卡最优任务序列以及等待时间。

由种群的平均适应度值变化趋势可以得出，集卡动态调度模型用遗传算法求解具有收敛性，并且种群中的每个子代中最大适应度值也趋于稳定，即随着代数的增加时间趋于平稳状态，显示了CHC算法在求解作业时间的优越性，此时的最大适应度值为fitmax=183，最小适应度为fitmin=168，平均适应度fitmean=172.78，对应的桥吊与集卡的染色体，即最优调度方案分别如表4和表5所示。

表4 岸桥(QC)的最优作业序列

表5 集卡(YT)的最优作业序列

从表4和表5可以得出，1号岸桥的作业序列为1→2→5→9→10→11，2号岸桥作业的序列为3→4→6→7→8→12;同时1号集卡作业序列为4→7→8→9→10→12，2号集卡的作业序列为11，3号集卡作业序列为3，4号集卡的作业序列为1→2→5→6。

最大完成时间由4辆集卡中最后一辆集卡的最大完成时间来决定，即max T=32，如表6所示。

表6 作业的开始、作业、结束时间

4 结论

笔者研究了考虑多种约束条件下的集卡与岸桥的协同调度问题，主要对卸箱作业过程，在考虑集卡作业的情况下做出岸桥的工作计划，并考虑了岸桥与集卡工作之间的优先约束，例如，不存在岸桥等待集卡的情况。由于NP－hard问题模型的复杂性，一般的优化算法不能求解。为此，引进了一个CHC算法来求解问题。通过算例测试，该算法能得到最优方案。

［1］B ISH E K，LEONG T.Analysis of a new vehicle scheduling and location problem［J］.Naval Research Logistics，2001(48):363 －385.

［2］B ISH E K.A multiple－crane－constrained scheduling problem in a container terminal［J］.European Journal of Operational Research，2003(144):83－107.

［3］徐 远琴，韩晓龙.集装箱码头集卡动态调度模型优化［J］.武汉理工大学学报:信息与管理工程版，2013，36(3):357 －360.

［4］N ISHIMURA E，IMAIA.Yard trailer routing at a maritime container terminal［J］.Transportation Research Part E，2005，41(1):53－76.

［5］张莉，霍佳震.基于单船装卸运输模型的集卡配置仿真研究［J］.系统仿真学报，2006(12):3532－3538.

［6］曾庆成，杨忠振.集装箱码头集卡调度模型与Q学习算法［J］.哈尔滨工程大学学报，2008，29(1):1 －6.

［7］KOO PH，LEEW S，JANG D.Fleet sizing and vehicle routing for container transportation in a static environment［J］.OR Spectrum，2004，26(2):193 － 209.

［8］张波，叶家玮，胡郁葱.模拟退火算法在路径优化问题中的应用［J］.中国公路学报，2004(1):79－83.

［9］CAO JX，SHIQ X，LEE D H.Integrated quay crane and yard truck schedule problem in container terminals［J］.Tsinghua Science and Technology，2010，15(4):467－474.

［10］CAO JX，LEE D H.The integrated yard truck and yard crane scheduling problem:Benders＇decomposition － based methods［J］.Transportation Research Part E，2010，46(3):344 －353.

［11］WOOYEON Y，EGBELU P J.Scheduling of inbound and outbound trucks in cross docking systems with temporary storage［J］.European Journalof Operational Research，2008(184):377 －396.

［12］EBRU K B，FRANK Y C.Dispatching vehicles in a mega container terminal［J］.OR Spectrum ，2005，27(3):491－506.