风电机组主轴承的设计与技术要求

张宏伟，闫瑞志，薛鹏，阚旭东

(1.大连冶金轴承股份有限公司，辽宁 瓦房店 116202；2.大连理工大学 机械工程学院，辽宁 大连 116024；3.中国航天万源国际(集团)有限公司，北京 100176)

风电机组发电机转子与轮毂连接部位的主轴承承担轮毂和叶片重量产生的径向力、倾覆力矩及风与叶片相互作用产生的轴向力、径向力、倾覆力矩，将风能产生的旋转力矩传递到风电机组发电机转子，带动发电机转子旋转产生电能。为了减小风机的体积和重量研发出的紧凑型风机，以及为提高发电质量研发出的直驱风机，都需要一种既满足较高工作转速又可以承受径向力、轴向力和倾覆力矩构成的交变载荷的主轴承。三排滚子转盘轴承是比较理想的风电机组主轴承的结构形式[1]。

1 结构设计原则

从风机主轴承的受力(图1)和载荷谱(表1)可知，其承受的径向载荷和倾覆力矩已成为影响其寿命的2个重要因素。该轴承的设计必须保证其具有较高的工作转速，匹配的径向、轴向承载能力，以满足其对承载能力和使用寿命的要求[2]。

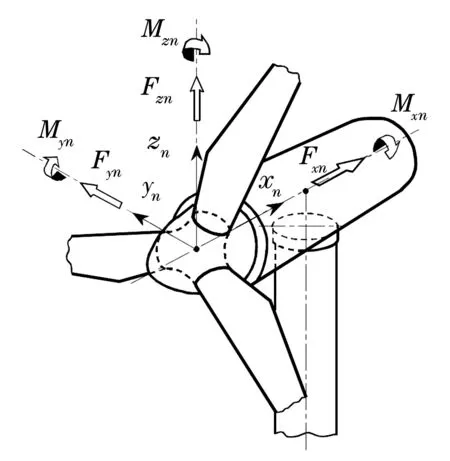
图1 风机主轴承的载荷坐标系

表1 风机主轴承载荷谱(总运行时间：175 000 h)

1.1 滚子尺寸的确定

由于安装空间的限制，三排滚子主轴承通过加大滚子直径提高自身承载能力和使用寿命的方法受到制约，因此在滚子直径一定时，主要通过加长滚子来提高自身的承载能力和使用寿命。轴向承载滚子随着长度的增加，滚子两端的线速度差也随之增加，势必加大滚子产生滑动的趋势，会对保持架施加载荷并产生发热现象，因此轴向承载滚子长度达到或超过1.5Dw(Dw为滚子直径)时，要采用双滚子配置。轴承的内、外圈结构近似环形梁，在倾覆力矩的作用下会产生变形；轴向游隙也会使套圈产生角位移，在变形和角位移的双重作用下，径向承载滚子会发生局部受载。在倾覆力矩和径向力共同作用下，径向承载滚子容易出现应力集中现象，且会随着滚子长度的增加而加重，因此径向承载滚子的长度达到或超过1.5Dw时，也应采用双滚子配置，以减小应力集中造成的影响。轴向、径向承载滚子的直径在初步确定时，应统筹考虑，根据安装空间在允许最大直径的前提下合理匹配，轴向与径向承载滚子的直径比一般为1∶(0.8～1)。考虑到主轴承承载能力和滚子的生产精度与经济性，应尽量选择Φ40～60 mm的滚子。

1.2 保持架结构的确定

三排滚子主轴承是否满足高速旋转的要求，保持架的结构是关键，其可靠性决定了轴承的可靠性。主轴承为水平轴线安装，运行时主轴承径向承载滚子的运行状态和承载形式与通用圆柱滚子轴承一致，因此保持架的结构也应同圆柱滚子轴承一样，轴承的内滚道作为保持架的引导面；轴向承载滚子除了绕主轴旋转外，在重力和离心力作用下会产生向下向外位移的趋势；轴向承载滚子的保持架在滚子重力和离心力作用下会向下拉长产生变形，因此保持架应采用有足够刚性的整体结构，以保证高速旋转时的稳定性，其宜采用内引导结构，边框应有足够的厚度以保证20年使用寿命对耐磨性的要求[3]。

2 材料的选择与技术要求

2.1 套圈材料的选择与热处理

套圈材料选用42CrMo4或在42CrMo4化学成分的基础上添加能够细化组织提高淬透性、力学性能的有益化学元素[3]。套圈需经过调质处理，调质处理前在能够保证加工余量和取样的前提下，应尽可能将套圈加工出接近成品的轮廓。调质硬度为260～310 HB；材料的最低力学性能应达到：抗拉强度σb=950 MPa，屈服强度σ0.2=700 MPa ，冲击功40 J；滚道采用中频表面淬火，表面硬度为59～62 HRC，有效硬化层深度大于5 mm， 58 HRC以上有效硬化层深度大于3 mm；软带宽度不超过18 mm。

2.2 保持架材料的选择

保持架材料选用强度高、耐磨性好且铝、铁、锰含量较高的铜合金。材料的最低力学性能应达到：抗拉强度σb=740 MPa ，屈服强度σ0.2=400 MPa，伸长率δ5=7%，布氏硬度170 HBW。

3 计算校核

3.1 滚道静安全系数与轴承疲劳寿命的校核

各种风机在设计时必须遵循国际上公认的认证要求才能进入市场运营，因此轴承滚道的静态安全系数与疲劳寿命也必须达到认证要求的数值。按照GL认证要求，滚道静安全系数大于1.5，轴承疲劳寿命按ISO 281的方法计算，为135 000 h，按ISO 16281的方法计算，为175 000 h。

3.1.1 滚道静安全系数的计算

按照风机提供的载荷谱(表1)选取极限轴向力、径向力、倾覆力矩，采用ISO 76的方法计算滚道静安全系数。

3.1.2 轴承疲劳寿命的计算

轴承疲劳寿命按ISO 281的方法计算时，需确定将倾覆力矩转换为轴向力的等效系数，等效系数的确定因计算理解上的差异而不同，建议进行轴承疲劳寿命的计算时采用ISO 16281的计算方法。

风机在设计时，通过设计软件计算出风机的轮毂与轴承连接凸缘的载荷谱，此载荷谱需经过简化与等效，变为能够满足ISO 16281计算方法的简化载荷谱(表1)。

风机在运行中，每种载荷状态下的运行转速和时间不同，对寿命的影响也不同，需要计算出工作时间百分比Pi，即

Pi=Ni/Nz，

Ni=niti，

式中：Ni为某种载荷状态下运行的转数；Nz为总寿命运行转数;ni，ti分别为某种载荷状态下的转速和运行时间；i=1，…，10。

将每一组合成后的轴向载荷、径向载荷、倾覆力矩和对应的工作时间百分比Pi按顺序输入计算软件界面，计算出轴承的寿命转数。将轴承的寿命转数与加权平均转速相除，得出轴承疲劳寿命。

3.2 套圈结构强度校核与加载变形的计算

3.2.1 套圈的有限元建模及网格划分

利用ANSYS的APDL语言对套圈进行参数化建模，得到的有限元模型如图2所示[4]。

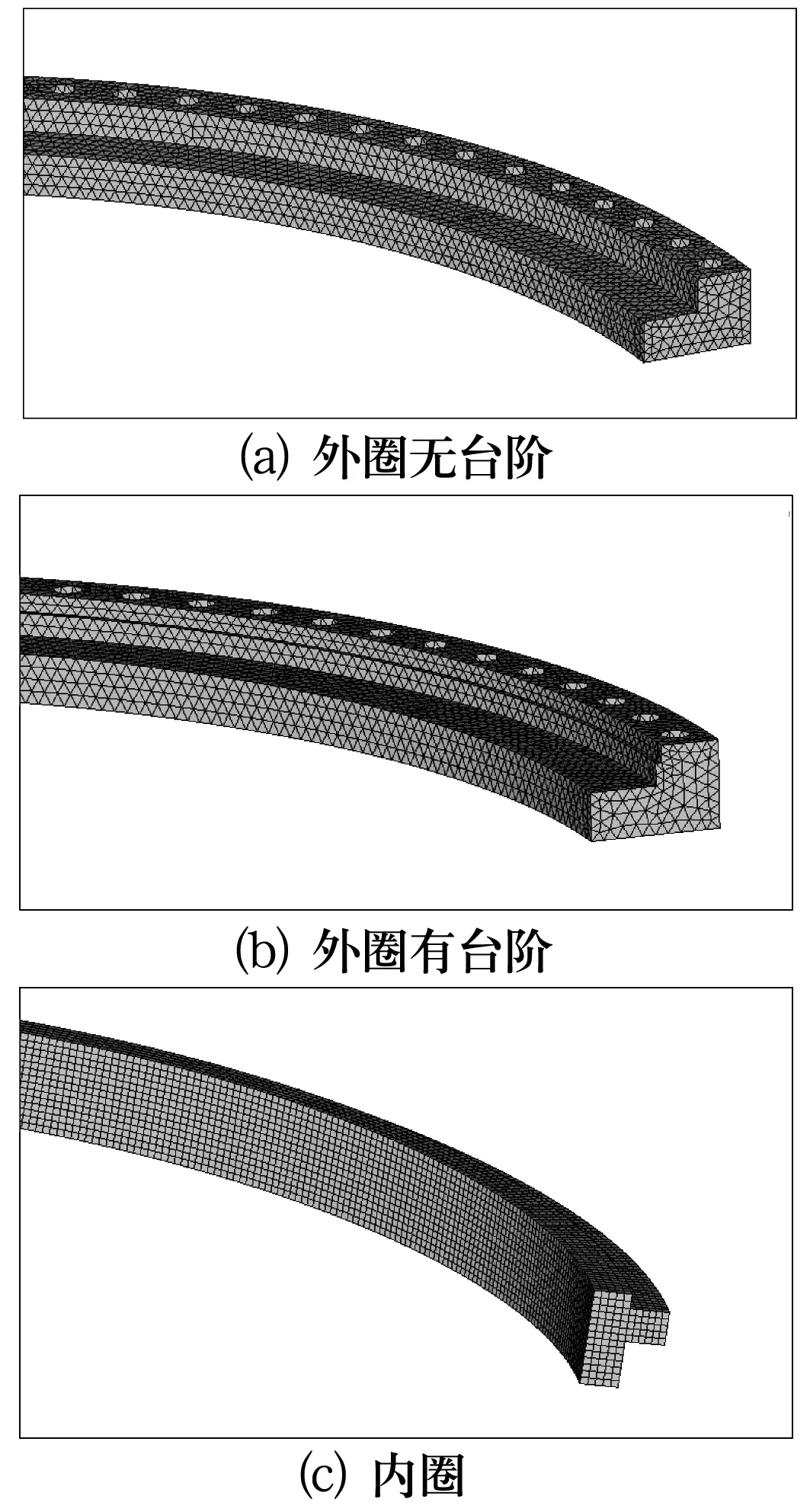
图2 单个套圈的有限元模型

3.2.2 边界条件

(1)双套圈结构中的单个套圈剖面的断面为对称受力、对称约束；2个套圈结合面、端面、安装螺栓为固定约束；

(2)单套圈结构中的单个套圈剖面的断面为对称受力、对称约束；端面、安装螺栓为固定约束。

3.2.3 有限元计算结果

通过有限元分析，计算出双套圈结构外圈的应力分布如图3a所示，位移云图如图3b所示；而单套圈结构内圈的应力分布如图4a所示，位移云图如图4b所示。确定套圈的最大变形是否小于允许的最大变形量；最大应力是否小于材料的许用应力[5]。

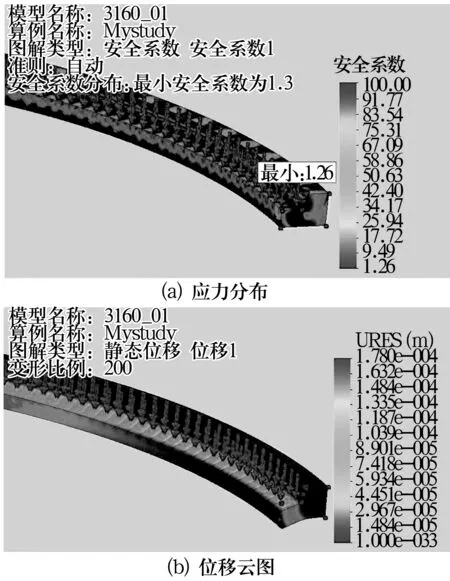
图3 双套圈结构的有限元计算结果

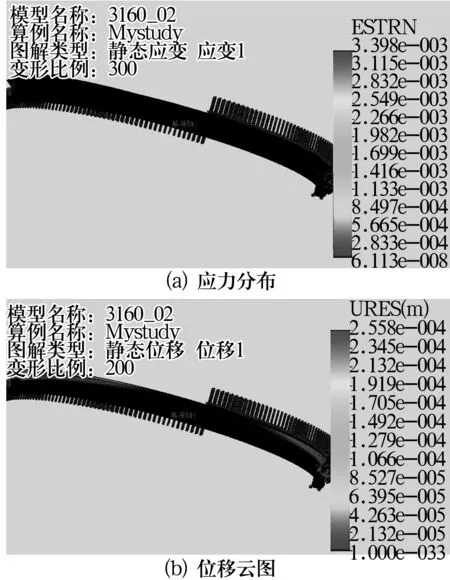
图4 单套圈结构的有限元计算结果

3.3 安装预紧后套圈变形量的计算与确认

3.3.1 套圈的有限元建模及网格划分

利用ANSYS建立套圈施加螺栓预紧后的模型，由于其为对称结构，为了便于分析，提高运算效率，建立一半模型。

在此采用8节点的Solid45单元对套圈进行网格划分，大小为30；为对接触区域进行细化，采用10节点Solid92单元对螺栓进行网格划分，得到的有限元模型如图5所示，经统计共有149 103个节点，423 134个单元。

图5 施加预紧后套圈的有限元模型

3.3.2 边界条件

根据有限元模型，双套圈结构中的单个套圈剖面的断面为对称约束，考虑模型的安装和工作条件，对于端面施加固定约束，而2个套圈的结合面和安装的螺栓面利用Target170目标单元和Contact174单元建立接触对。建立的接触对模型如图6所示。

图6 接触对模型

3.3.3 受力分析与计算

基于此处是考虑螺栓预紧对套圈变形量的计算，结合实际应用，采用10.9级的高强度螺栓。

螺栓预紧力为

(1)

式中：k为拧紧力系数；σS为螺栓材料的屈服极限；AS为螺栓危险界面的面积；d1为螺栓危险剖面的计算直径。

根据设计要求，选取k=0.7，σS=900 MPa，得到需要施加的螺栓预紧力。

3.3.4 有限元计算结果

通过非线性的迭代运算，得到的整体位移云图如图7a所示，上排滚子与套圈接触面的局部位移云图如图7b所示。

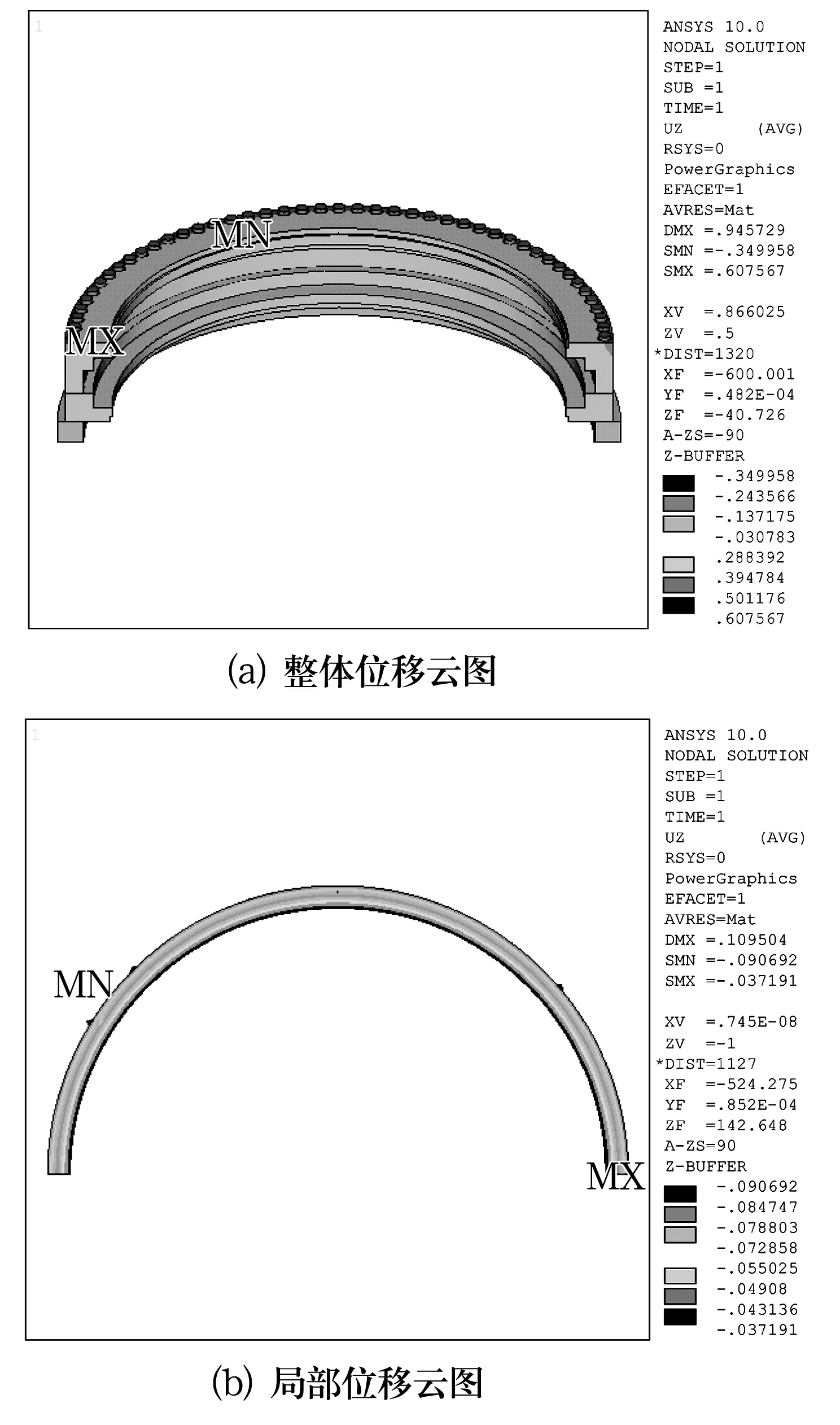
图7 有限元分析结果

3.4 保持架工作变形量的计算与确认

3.4.1 有限元建模及网格划分

保持架采用三维制图软件Pro/E进行实体建模，如图8所示。

图8 保持架实体模型

实体单元类型选取Solid45，单元尺寸设置为5 mm。得到保持架有限元模型如图9所示，共有68 856个节点，240 290个单元。

图9 保持架有限元模型

3.4.2 保持架受力分析与计算

根据设计的三排圆柱滚子轴承结构可知，轴承水平轴线安装，此时保持架受力有[6]：(1)滚子和保持架旋转而产生的离心力；(2)因保持架和滚子的重力作用而产生的附加径向偏心离心力；(3)保持架和轴向承载滚子的重力。

3.4.2.1 附加径向偏心离心力计算

保持架受自身和滚子重力的影响会产生沿垂直方向的偏移量e，进而产生垂直向下的附加径向偏心离心力。该离心力为

F=mv2/r，

(2)

式中：m为物体质量，kg；v为运动物体的线速度，m/s；r为物体质心距旋转中心的距离，m。

根据角速度与线速度的转化关系v=πdn/60，并将提供的风电主轴承的相关参数代入(2)式中，计算可得保持架处于最大偏心位置时产生的附加径向偏心离心力为

(3)

式中：mw为轴向承载滚子的总质量；mb为轴向承载滚子保持架的总质量；na为轴向承载滚子中心转速;ea为轴向承载滚子保持架的最大偏心量。

3.4.2.2 旋转离心力计算

保持架的旋转离心力为所有轴向承载滚子和保持架的旋转离心力之和，且离心力沿径向均匀分布，其计算过程如下。

(1)滚子旋转离心力计算。钢制滚子的离心力为[7]

(4)

式中：Dw为滚子公称直径；l为滚子长度；Dpw为滚子组节圆直径；nm为滚子公转速度。

根据无滑动条件，在接触点处滚子与滚道表面线速度相同，因此轴向承载滚子与内滚道的接触点C的实际线速度为

(5)

式中：dc为C点所在圆直径，dc=Dpw；ni为内圈实际转速。

由于外圈固定，内圈旋转，轴向承载滚子与外滚道的接触点D的实际线速度vD=0。根据滚子直径CD上的速度分布可得滚子中心点的实际线速度为

(6)

而va也可表示为

(7)

式中：ωm为轴向承载滚子公转角速度。

在风电主轴承最大工作转速下(ni=22 r/min)，由(6)和(7)式得轴向承载滚子的公转速度为

(8)

则在风电主轴承最大工作转速下，可由(4)式求出每个滚子的离心力。

(2)保持架旋转离心力计算。由轴承运动学关系可知，保持架的转速与滚子公转速度nm相同，为11 r/min。

则保持架旋转离心力为

(9)

式中：ma为保持架的质量。

总的旋转离心力为

(10)

3.4.2.3 保持架所受重力计算

保持架每个兜孔位置还受一个滚子重力的作用，保持架整体所受重力值为所有滚子重力和保持架重力之和，方向垂直向下。

3.4.3 边界条件

保持架通过内圈接触面来约束其径向位移的变化，通过端面控制其轴向位移。在实际的运动过程中，保持架内圈的上半段都有可能与内圈引导面接触，结合实际接触范围，在此选取了内圈上半段的一半施加全约束。

3.4.4 有限元计算结果

经过有限元计算，得到的整体变形云图如图10所示。

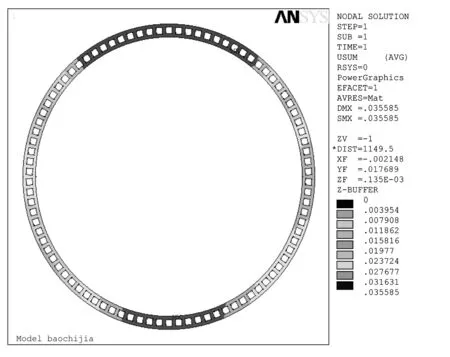
图10 保持架变形云图

4 结构设计的修正与确认

根据滚道静安全系数与疲劳寿命的校核数据确定滚子尺寸，根据套圈结构强度的校核与加载变形的计算确定各个滚道厚度与游隙。

4.1 滚子尺寸的确定

采取“穷极法”逐渐增大滚子直径进行计算，直至满足寿命要求；若达到结构允许的最大直径时，仍未满足寿命要求，则逐渐增大滚子长度进行计算，直到满足寿命要求。

由于采取“穷极法”的计算量比较大，因此采用以ISO 281中轴承疲劳寿命计算方法为基础的计算软件进行计算和分析，可以提高效率和计算精度。虽然按照GL认证要求，轴承疲劳寿命分别按ISO 281 和ISO 16281的方法计算应为135 000，175 000 h，但是由于轴承套圈的应力变形，径向承载滚子会出现应力集中现象，因此径向承载滚子尺寸达到轴承疲劳寿命后，长度应增加30%，以确保轴承的实际使用寿命达到要求[8]。

4.2 轴承轴向游隙的确定

在实际工作状态下主轴承的轴向承载滚道处于轻微过盈的状态。轴承装配轴向游隙在安装使用时会被双套圈组合外圈的预紧变形量抵消，因此轴承装配轴向游隙由安装预紧后套圈的变形量决定。通过对双套圈组合外圈在预紧力作用下变形量的计算，计算出2个滚道的位移量，将装配轴向游隙定为预紧力作用下2个滚道之间尺寸减小的数值[9]。

4.3 保持架与外圈间隙的确定

该轴承的保持架尺寸较大，刚性较差，在离心力的作用下非常容易变形。为避免工作过程中保持架与外圈的接触碰撞，降低保持架的磨损，保持架与外圈的间隙要大于保持架高速旋转时的最大变形量。通常将保持架与外圈的间隙定为保持架高速旋转时最大变形量的1.2～2倍。

5 结束语

通过对风电机组主轴承所受载荷的分析，运用有限元分析软件和转盘轴承计算软件对三排滚子主轴承的结构强度、刚性以及寿命进行分析计算，能够使主轴承的设计得到校核，依据校核数据对轴承结构进行的优化能在理论上为保证轴承的使用寿命奠定基础。实际生产时，通过对实物零件的测试，校对理论计算时的参数，并对理论计算值加以调整，使理论计算更加贴近实际，产品更加可靠。这种三排滚子主轴承的设计方法还可以推广到有近似载荷工况的盾构机主轴承的设计中。