强度折减法在含软弱结构面岩坡稳定性分析中的应用
2014-07-21张云杰
卜 林,徐 涛,2,张云杰
(1.大连大学 材料破坏力学中心,辽宁 大连 116622;2.东北大学 岩石破裂与失稳研究中心,沈阳 110004)
岩坡的稳定性分析历来是引人关注的重大课题。由于工程实际中的岩质边坡包含大量的不连续结构面(例如节理、硬性结构面、裂隙、断裂破碎带、岩脉以及软弱夹层等),给岩质边坡的稳定性分析带来了非常大的困难。郑颖人等[1-2]将基于强度折减的有限元法引入有限元计算,为含软弱结构面及节理的岩质边坡问题的分析与研究开辟了新的途径。
本文将应用ABAQUS软件进行含软弱结构面的岩质垂直边坡的安全稳定性分析,描绘出坡体塑性变形及水平位移随荷载增加的情况以及塑性区的萌生与发展,由以上所述的分析结果来评价含软弱结构面岩质边坡的稳定性以及相应的安全系数。
1 有限元强度折减法分析的基本原理
用有限元强度折减法分析边坡稳定性的基本原理是:在弹塑性有限元计算过程中将反映岩土体强度的指标C、Φ值除以相应的折减系数F,把得到的一组新的C’、Φ’值作为新的材料参数重新代入到有限元程序中进行计算,当边坡岩土体符合所给定的临界破坏状态的判定条件时,对应的F被称作边坡的最小安全系数,参数C、Φ分别由式(1),(2)求得,而弹性模量E和泊松比v在计算中假设为定值,不随C、Φ 值的变化而变化[3]。

2 有限元法边坡稳定性评判依据
2.1 屈服准则的选取
影响边坡失稳破坏的决定性因素是边坡岩土体的抗剪强度,当最大剪应力达到边坡岩土体的破坏极限时,边坡就会发生失稳破坏。本文采用有限元强度折减系数法求解边坡稳定问题时,采用的是理想的弹塑性模型,屈服准则采用的是Mohr-Coulomb准则:

式中:I1—应力张量的第一不变量;J2—应力偏张量的第二不变量;θσ—应力罗德角;φ—岩土体的内摩擦角;C—岩土体的黏聚力。
2.2 流动法则的选取
Mohr-Coulomb准则的塑性势方程为:

式中,σm为平均应力;ψ为剪胀角且0≤ψ≤Φ。当ψ=0时没有剪胀现象,ψ=Φ时即为 Mohr-Coulomb屈服条件,具有最突出的剪胀现象。本文采用非关联的流动法则,取剪胀角ψ=0。
2.3 边坡失稳的判断依据
边坡岩体的塑性破坏主要与边坡岩体的塑性区出现、发展以及其重分布紧密相关,而塑性应变能够较好地反映出岩体塑性区的萌生、发展与破坏过程,因此本文将塑性应变作为评判边坡失稳的指标,根据塑性区的出现范围以及连通程度来确定边坡潜在滑动面及安全系数,评价含软弱结构面边坡的稳定性[4-5]。
3 算例分析
分别对岩坡中软弱结构面的几何位置,以及结构面间的岩桥长度等方面进行数值模拟,分析验证前述分析方法的合理性与实用性。选取如图1所示的以典型边坡作为算例,岩坡高25m,坡脚β=90°,采用ABAQUS软件进行具体的模拟计算。岩体与软弱结构面的参数如表1所示。

表1 材料参数Table 1 Material parameters

图1 数值模型Fig.1 Numerical model
岩体及结构面采用理想弹塑性模型,屈服准则采用Mohr-Coulomb准则,采用四节点平面应变单元(CPE4),限制模型两侧的水平位移和模型底部的水平与垂直位移。
3.1 含两条条未贯通结构面的岩坡算例
模型如图2(a)所示:在距离坡脚5m高处有一外倾软弱结构面,结构面倾角为45°,AB=5m,AB与CD的垂直距离BC=10m,CD=7.76m,结构面AB和CD的倾角均为45°。通过有限元强度折减得到的破坏形式如图2所示。
塑性区最开始出现在CD结构面的下端,随后结构面AB上端也开始出现塑性区,之后两边的塑性区逐渐在岩桥间扩展,出现塑性区的贯通现象。在此过程中,贯通区之上部分的位移量也逐渐增大,贯通区上的单元逐渐破坏,直至最后形成了破裂面。出现塑性区贯通区时对应的安全系数3.79。对剪应力云图分析可得,结构面AB、CD间的岩桥上的点在塑性区贯通时的剪应力分别为:C点0.209 MPa,E点0.241MPa,B点0.231MPa。由此可以看出,当两条软弱结构面之间岩桥为垂直时,岩桥中部单元所受剪应力最大,下部单元其次,上部单元最小。由图2中的边坡失稳时的增量位移图可以很清晰地判断出边坡失稳时的滑动面。

图2 含两条软弱结构面的岩坡数值模拟(a)软弱结构面分布;(b)塑性区分布;(c)剪应力分布;(d)坡顶增量位移图Fig.2 Simulated result of rock slope with two weak structure planes(a)distribution of the weak structure plane;(b)distribution of plastic zone;(c)distribution of shear stress;(d)incremental displacement on top of the slope
4.2 含三条结构面的岩坡算例
如图3所示,在图2(a)的基础上增加与CD平行的结构面EF,AB与EF共线。通过有限元强度折减得到的破坏形式如图3所示。
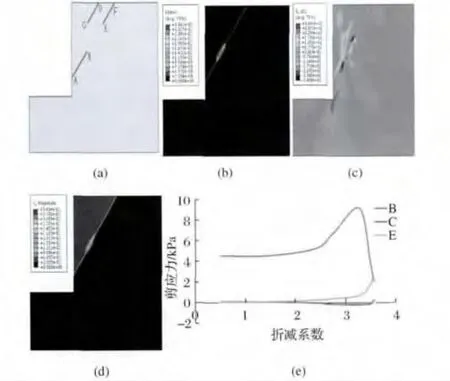
图3 含两条软弱结构面的岩坡数值模拟(a)软弱结构面分布;(b)塑性区分布;(c)剪应力分布;(d)坡顶增量位移图;(e)岩桥上不同位置的剪应力随折减系数的变化情况Fig.3 Simulated result of rock slope with two weak structure planes(a)distribution of the weak structure plane;(b)distribution of plastic zone;(c)distribution of shear stress;(d)incremental displacement on top of the slope;(e)shear stress-reduction coefficient curve on different positions of rock bridge
有三条结构面的情形,塑性区最先出现在结构面AB的上端和结构面EF的下端,随后塑性区不断在岩桥中扩展,最后破坏滑动面在结构面AB与EF之间贯通。边坡破坏时对应的安全系数为3.5。滑动面在AB与EF间贯通,是因为AB与EF贯通之后形成了直线滑动面,这是使坡体更容易发生破坏的形式。由图4可以看出,在有限元分析的折减步中整个岩桥上单元所受剪应力总体呈逐渐增大趋势,不同的单元又受不同的剪应力:BE间的岩桥所受剪应力较大,岩桥下部单元B点的剪应力又明显高于岩桥上部单元E点的剪应力。随着折减系数的增大,当达到边坡失稳时的折减系数时,贯通的岩桥间单元的剪应力开始减小。而处于非贯通区的C点,剪应力状态则变化不大。
将图3(a)中的结构面EF平行右移2m,如图4(a)所示。

图4 含两条软弱结构面的岩坡数值模拟(a)软弱结构面分布;(b)塑性区分布;(c)剪应力分布;(d)坡顶增量位移图;(e)岩桥上不同位置的剪应力随折减系数的变化情况Fig.4 Simulated result of rock slope with two weak structure plane(a)distribution of the weak structure plane;(b)distribution of plastic zone;(c)distribution of shear stress;(d)incremental displacement on top of the slope;(e)shear stress-reduction coefficient curve on different positions of rock bridge
虽然AB与EF贯通会产生直线滑动面,但是AB与CD之间的岩桥长度(5m)要小于AB与EF之间的岩桥长度(8.7m)。由有限元强度折减分析得出AB与CD最先贯通。安全系数3.32。由图4可以看出,处于最后贯通区岩桥上的B点与C点剪应力一开始逐渐增大,直至贯通区形成后开始减小。岩桥下部单元B点的剪应力明显高于上部单元C点的剪应力。图5(a)中,BC=10m,BE=8.5m,通过有限元强度折减发现,虽然结构面AB与结构面EF距离较近,但结果却是AB与CD最先贯通,这是因为结构面AB与CD贯通后,形成的是直线滑动面。这说明岩桥两端软弱结构面倾角与结构面之间岩桥的倾角越相近,岩桥越容易破坏、贯通并形成滑动面,而直线破坏形式的滑动面最容易贯通与滑动。此时的安全系数为4.2,由图5(e)可以看出,当折减系数逐渐增大时,结构面上各处计算单元的剪应力呈逐渐增大的趋势,当在岩桥中形成塑性贯通区后,结构面上的剪应力开始逐渐减小,破坏滑动面上B点和C点的剪应力明显大于处于非贯通区E点的剪应力。
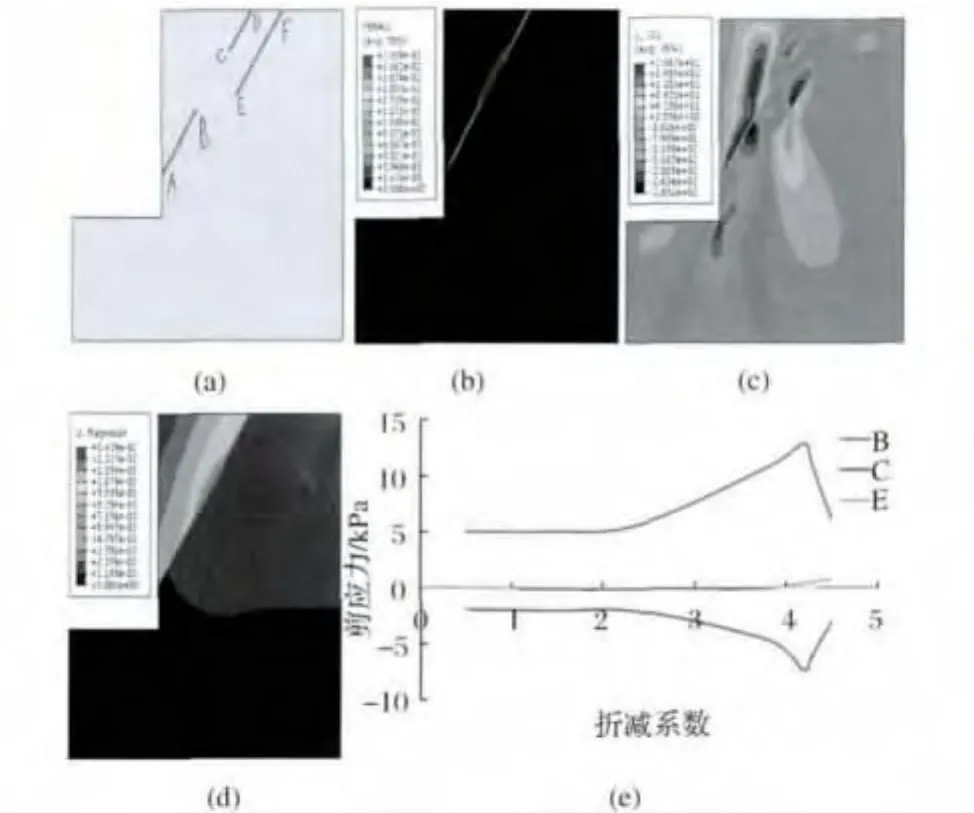
图5 含两条软弱结构面的岩坡数值模拟(a)软弱结构面分布;(b)塑性区分布;(c)剪应力分布;(d)坡顶增量位移图;(e)岩桥上不同位置的剪应力随折减系数的变化情况Fig.5 Simulated result of rock slope with two weak structure planes(a)distribution of the weak structure plane;(b)distribution of plastic zone;(c)distribution of shear stress;(d)incremental displacement on top of the slope;(e)shear stress-reduction coefficient curve on different positions of rock bridge
如图6(a)所示,结构面CD倾角为70°,B与C垂直共线,AB与EF共线,BC=5m,BE=10m。

图6 含两条软弱结构面的岩坡数值模拟(a)软弱结构面分布;(b)塑性区分布;(c)剪应力分布;(d)坡顶增量位移图;(e)岩桥上不同位置的剪应力随折减系数的变化情况Fig.6 Simulated result of rock slope with two weak structure planes(a)distribution of the weak structure plane;(b)distribution of plastic zone;(c)distribution of shear stress;(d)incremental displacement on top of the slope;(e)shear stress-reduction coefficient curve on different positions of rock bridge
由模拟结果可知,结构面AB与CD间的岩桥距离(5m)比AB与EF间的岩桥距离(10m)小,塑性区在结构面AB与CD的末端率先出现,并贯通其之间的岩桥,最终形成塑性贯通区。说明相同的情况下,岩桥长度越短,岩桥就越容易贯通形成滑动面。此时的安全系数为3.8.对应于滑动面BC上B点和C点的剪应力明显大于处于非滑动面E点处的剪应力。如图7(a)所示,BC=10m,BE=7m,B与E水平共线。
图7表明,塑性区由坡脚处开始出现并逐渐向上延伸形成了圆弧状的滑动面,该滑动面与软弱结构面EF相贯通并最后形成了一个完整的滑动面。尽管软弱结构面AB与EF间的岩桥距离最短,但是此岩桥为水平方向,与软弱结构面AB与软弱结构面EF形成的夹角比较大,可以形成的是折线形式的滑动面。结构面AB和CD的方向一致,且软弱结构面AB与CD间距离小于软弱结构面EF到边坡坡脚的距离,因为岩坡坡脚处的剪应力较大,滑动面也没有在软弱结构面BC处通过,而是在边坡坡脚的位置发生了贯通破坏。此时的安全系数为4。由图7(e)可以看出,坡脚的剪应力明显大于岩桥个点的剪应力,这也说明了贯通区在坡脚出现的原因。
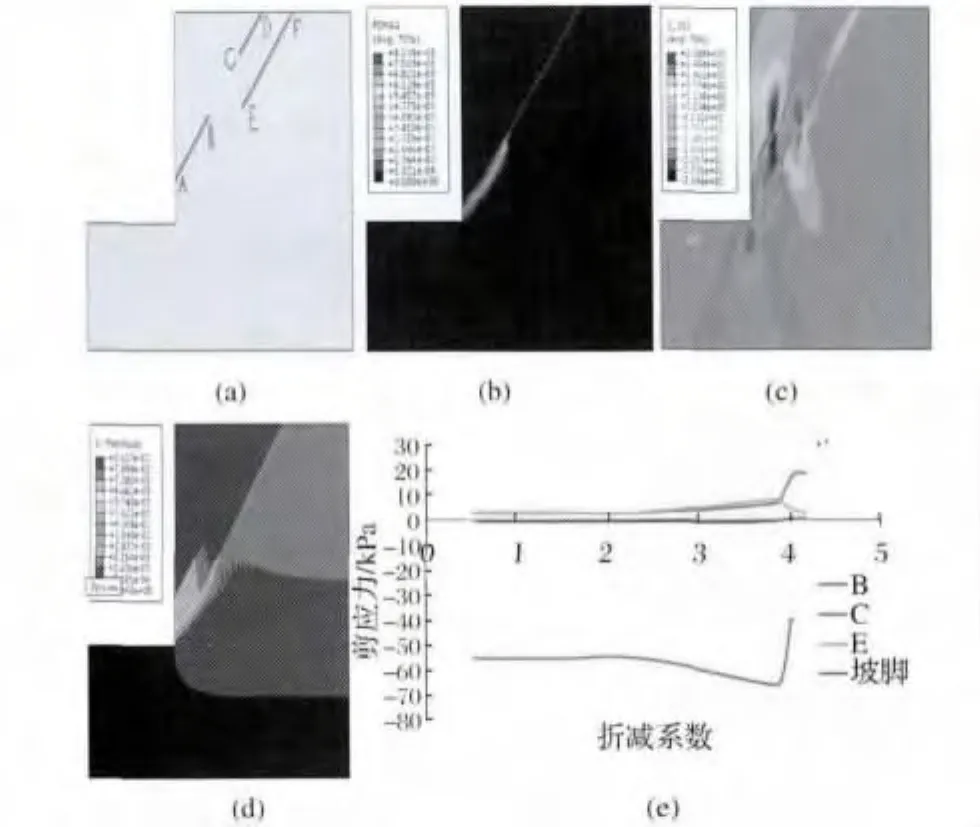
图7 含两条软弱结构面的岩坡数值模拟(a)软弱结构面分布;(b)塑性区分布;(c)剪应力分布;(d)坡顶增量位移图;(e)岩桥上不同位置的剪应力随折减系数的变化情况Fig.7 Simulated result of rock slope with two weak structure planes(a)distribution of the weak structure plane;(b)distribution of plastic zone;(c)distribution of shear stress;(d)incremental displacement on top of the slope;(e)shear stress-reduction coefficient curve on different positions of rock bridge

图8 不同结构面分布形式时的折减系数—坡顶水平位移图Fig.8 The horizontal displacement-reduction coefficient curve of different distributions of the weak structure planes
图8为以上5种存在三条软弱结构面的不同分布情况时的折减系数—坡顶水平位移图,其中的坡顶位移指边坡模型坡顶的左上角点的水平位移。由于当折减系数到达最终的安全系数时,随着塑性区在边坡破体内的贯通,会形成滑动面,继而边坡失稳,而坡顶的水平位移能很好地反映边坡由稳定状态至最终破坏的过程。由图8可以看出,在折减步中当坡体内的塑性区由萌生至发展的过程中,坡顶的水平位移基本为0,随着塑性区在坡体内贯通(即折减系数等于安全系数)时,坡顶的水平位移开始迅速增加,表明此时边坡已经进入了破坏的状态。通过图中结构面不同分布情况下的安全系数的大小比较可以发现:1)岩桥两端结构面的倾斜角度与岩桥的倾斜角度越接近时,岩桥越容易破坏贯通,从而形成滑动面,最容易贯通破坏的形式是直线滑动面。2)岩桥长度越短时,岩桥间的软弱结构面越容易贯通破坏。3)受剪应力越大的地方越容易发生贯通破坏,即使受力大的地方不存在软弱结构面,滑动面依然会通过剪力较大的区域,例如坡脚处。
5 结论
将强度折减法与ABAQUS软件的非线性分析相结合,以岩质边坡中塑性区的贯通作为边坡失稳的评判依据,利用ABAQUS计算结果的显示技术,对平面应变条件下的岩坡稳定性进行了数值分析计算,直观地得到了土坡的塑性滑移带,并求得了相应的安全系数,为准确判定边坡的滑动面及相应的安全系数提供了可靠的依据。为准确考虑结构面的影响,分别对含单一软弱结构面、两组软弱结构面、三组软弱结构面的岩坡进行了模拟计算,针对岩坡中软弱结构面的贯通率、几何位置、以及结构面间的岩桥长度等方面,进行了分析,证明了软弱结构面是在岩质边坡破坏过程中起主要作用的控制因素,软弱结构面之间的贯通机制受结构面之间岩桥的长度、倾斜角度以及结构面的倾斜角度、几何位置等因素的影响。在其它因素相同的情况下:1)岩桥两端结构面的倾斜角度与其间岩桥的倾斜角度越接近,软弱结构面间的岩桥越容易贯通从而形成滑动面;2)岩桥长度越短时,岩桥越容易贯通破坏;3)受力越大的地方越容易破坏,比如坡脚处。结构面在相互贯通过程中,岩桥上不同点的剪应力总体呈增大趋势,岩桥上部单元的剪应力水平明显大于下部,当形成塑性贯通区时,岩桥上的剪应力将逐渐减小。
[1] 郑颖人,赵尚毅 .有限元强度折减法在土坡和岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.
[2] 赵尚毅,郑颖人,时为民,等 .用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.
[3] 张绪涛 .ABAQUS强度折减法在边坡稳定分析中的应用[J].人民长江,2009,5(9):62-64.
[4] 栾茂田,武亚军,年延凯 .强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1-8.
[5] 刘金龙,栾茂田,赵少飞,等 .关于强度折减有限元方法中边坡失稳判据的讨论[J].岩土力学,2005,26(8):1345-1348.
