基于MPC的液压混合动力车辆能量管理策略研究

李顶根，严 索，高幼民，苗华春

（1.华中科技大学 能源与动力工程学院，武汉430074；2.襄樊宇清电动汽车有限公司，襄阳441021）

基于MPC的液压混合动力车辆能量管理策略研究

李顶根1，严 索1，高幼民2，苗华春2

（1.华中科技大学 能源与动力工程学院，武汉430074；2.襄樊宇清电动汽车有限公司，襄阳441021）

针对双轴并联式液压混合动力车辆（PHHV），以蓄能器荷电状态(SOC)和发动机瞬时燃油质量流量 为输入量,发动机需求功率比例φ为输出量，以油耗最小为目标函数设计了模型预测控制器（MPC）进行PHHV的能量管理。基于MATLAB/Simulink平台搭建了包括需求功率计算、发动机、蓄能器和泵/马达等主要部件的PHHV车辆模型并进行MPC能量管理。研究结果表明,在美国道路城市循环工况（UDDS）下， MPC管理下的PHHV能充分发挥混合动力的特点，合理调节分配发动机和液压单元的需求功率，降低行驶过程的总油耗。

液压混合动力（PHHV）；能量管理；模型预测控制（MPC）

传统车辆在能源消耗和环境污染方面存在巨大问题。利用新能源的风能车和太阳能车尽管节能环保,但是由于技术的限制,其发展前景并不明朗[1]。液压混合动力车辆由于能回收利用制动能量,具有工作效率高、燃油消耗少和尾气排放少的优势,已经吸引了各大主流汽车厂商以及研究机构的注意。学者Delprat的研究表明混合动力车辆的能量管理问题最终要落实到功率和转矩的分配问题上来[2]，众多科研工作者对混合动力技术能量管理策略的研究也逐渐从速度控制转向了功率和扭矩的研究,并且不断有新的管理策略出现。

现阶段的研究情况大致可以分为四类：基于规则法的能量管理策略、瞬时最优法能量管理策略、全局最优法能量管理策略以及智能型能量管理策略。规则法主要是通过门限值来确保发动机工作在高效区，但这种方法过于简单，无法保证系统各部件能达到最佳匹配的状态[3]。瞬时优化法和全局优化法都是基于对系统等效燃油的优化，但前者计算量过大，后者需要限制在特定工况[4，5]。智能型能量管理策略虽然能模仿人处理问题的分析、推理以及决策过程，但需要采集大量数据用作先验经验[6]。本文基于MATLAB/Simulink平台，建立了并联式液压混合动力车辆模型和模型预测控制器，研究了MPC的能量管理策略对PHHV燃油性的影响。

1 PHHV车辆模型

本文研究对象为双轴并联式液压混合动力车辆，简化原理示意图如图1所示。

1.1 需求功率计算模型

研究不涉及混合动力车辆的操纵性问题，忽略车辆的横向运动，故研究只局限在一维范围，即将车辆简化为一固定质量的方块，得到一个单自由度模型。车辆在行驶过程中，受到四种阻力，有轮胎滚动阻力、空气阻力、爬坡阻力和加速阻力。由循环工况所要求的需求功率 ：

式中：P为作用于滚动车轮中心铅垂方向的载荷；fr为滚动阻力系数；α为路面的倾斜角度；v为车速；ρ为空气密度；A为车辆迎风面的正面面积；CD为与车身形状有关的空气阻力系数；M为车辆的质量；g为当地重力加速度；a为车辆的加速度；f（u）为车辆的质量系数。

1.2 发动机模型

现阶段常用的发动机建模方法是通过实验来获取发动机的外特性曲线和万有特性曲线等相关数据，建立类似于MAP图的数据表格。然后在模型仿真运行过程中，通过快速的插值和查表，得到发动机运行所需的相关参数和数据。但这种方法建模所需要的数据都基于台架稳态实验，忽略了发动机的动态效应，此外建立的模型也仅适用特定的发动机[7]。理论建模则是基于发动机特征参数，利用流体力学、热力学以及动力学原理来建立发动机的燃油流量方程，甚至会涉及到复杂的燃烧理论和各部件的热传递问题等。这种建模方法有个最大的好处是模型的移植性更强,只要修改发动机的相关几何尺寸参数就能很方便的应用于其它型号发动机上。本研究采用理论建模法建立的发动机模型如图3所示，模型的输入量为车速、发动机需求功率，输出量为瞬时燃油消耗量、输出转矩值。

研究对象为柴油机，缸内理想循环为等压循环，即狄塞尔循环。热效率为 ：

式中：rc为 压缩比；rcut为膨胀比；k为绝热指数。

发动机角速度we为：

式中：v为车辆速度；if为 传动系传动比；ig为变速器传动比；r为车轮半径。

发动机缸内的摩擦损耗功率[8，9]：

式中：cm为 活塞工作行程；ne为 发动机转速；Vs为发动机排量；ρs为缸内燃气密度，理想情况下取ρs=1 000。燃料质量流率 ：

式中：Hu表 示柴油热值；ηm为机械效率。

1.3 液压单元

理想气体状态方程:

定义蓄能器中氮气体积Vi时 的能量SOCi：

式中：Va表示氮气膨胀至最大程度时的气体体积；Vmin表示氮气压缩至最小程度时的气体体积；SOC为0时，表示蓄电池当前存储的能量为0；SOC为1时，表示蓄电池充满了能量。SOC值越大表示针对该蓄电池,其当前所储存的能量值越多。

波义尔气体定律：

式中：V1表示气体压强为p1时的气体体积；V2表示气体压强为p2时的气体体积；n为气体多变指数，等温过程中n=1，绝热过程中n=1.4 。

能量方程：

式中：cv为氮气比热容；T为氮气温度；p为氮气压强；V为氮气体积。

式中：Q为液压流体的流量。在工作过程中假设液压流体为不可压缩，则单位时间内液压流体流过的体积等于蓄能器中氮气体积的变化量。Q>0时液压单元以马达形式工作，Q<0时液压单元则工作在泵状态。

首先根据氮气预加压压力和初始温度，由理想气体状态方程求得氮气膨胀至最大程度时的气体体积Va。然后对液压泵/马达的流量Q进行积分，可以得到蓄能器内氮气体积。由能量方程积分后得到温度。将氮气温度、质量、体积代入理想气体状态方程后计算得到氮气压力。最后由公式（11）求得蓄能器功率。所建立的蓄能器模型如图4所示。

液压泵/马达角速度wh：

式中：v为车辆速度；r为车轮半径；if为传动系传动比；ih为变速器传动比。

液压泵/马达的转矩Th：

式中： Δp是高压蓄能器与低压蓄能器的压力差，由于高压蓄能器中的压力远远大于低压蓄能器中的压力，故可以将 Δp近似为高压蓄能器中的氮气压力p。D是液压泵/马达的排量，那么通过液压泵/马达的流量Q：

所建立的液压泵/马达模型如图5所示。

1.4 主要参数

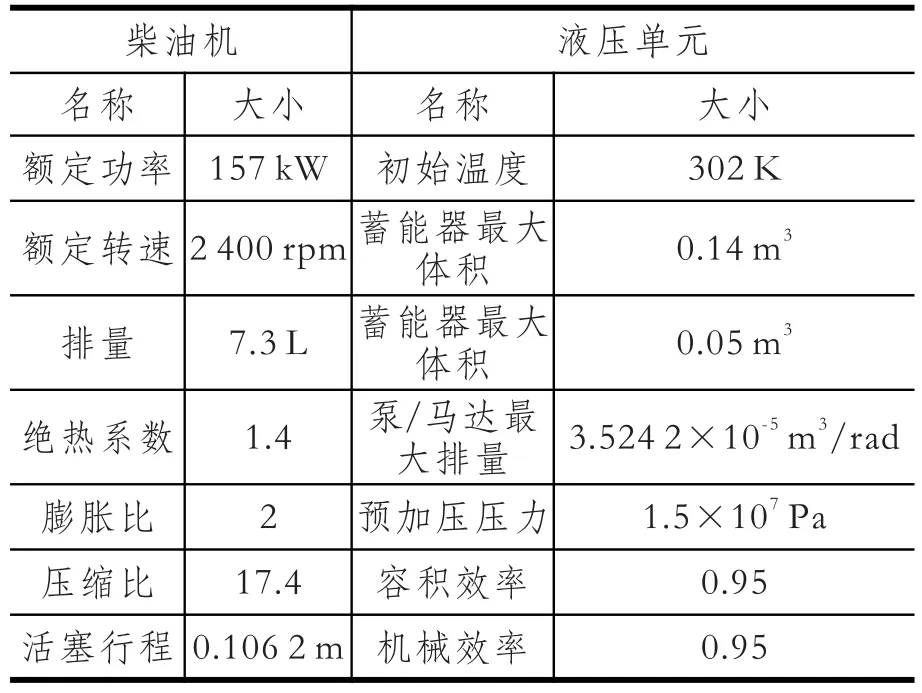
表1 动力系统主要参数

2 MPC能量管理策略

产生于20世纪70年代的模型预测控制技术（MPC）发展至今已取得很大成功。近几年，有学者逐渐将其应用至内燃机控制领域。Joachim Ferreau和Ortner等人[10]利用MPC能有效处理带约束和耦合的多输入多输出模型控制问题的特点，控制柴油机废气再循环（EGR）阀和可变几何截面涡轮（VGT）阀。M Karlsson, K Ekholm等人[11]将系统辨识和MPC控制进行结合，通过辨识建立了柴油机的5输入4输出系统，系统的研究了MPC在发动机控制方面的实际应用。

2.1 基本原理

MPC算法有三个主要的组成部分：预测模型、滚动优化和反馈校正。在k采样时刻，首先预测模型根据系统过去的输入输出信息预测系统未来Hp时间内的输入输出信息；再对预测域Hp内的目标函数进行最优化计算得到控制域Hc，并施加于系统；最后利用系统输出对模型进行反馈，修正由于系统干扰和模型失配导致的优化基准点失真，甚至控制失常。在下一个采样点，重复上述步骤，实现滚动优化。

2.2 控制器设计

在任意k采样时刻,车辆通过预测模型预知接下来的p时间长度内，即[k，k+p]时间段内车辆的状态,通过优化计算[k，k+p]范围内的目标函数得到控制序列,然后将控制序列的前q项应用于控制域。由于循环工况已知，故将车速v和车辆总需求功率设置为可测干扰。输入量为蓄能器荷电状态SOC值和发动机瞬时燃油质量流量，输出为发动机需求功率比例系数φ。泵/马达需求功率为总需求功率减去发动机需求功率，如图7。

将发动机需求功率比例系数定义为模型预测控制的控制变量h（i）:

系统状态转移方程为:

以预测域内消耗的等效燃油最小为目标建立目标函数 :

式中：L（ x （ i ） ， h （ i ） ， i ） Δ t 为发动机消耗的燃料与蓄能器SOC变化时的等效燃油消耗量之和。蓄能器SOC增大时其等同于蓄能器的等效燃油消耗为负,表示蓄能器正在充能,间接节省燃油；蓄能器SOC减小时其等效燃油消耗量为正,表示蓄能器正在释放能量,消耗能量。

在每一个采样时刻k,通过优化目标函数 使其最小来得到控制序列,然后将控制序列的前q项应用于控制域,一般只取第一项。而到了下一个采样时刻k+1,预测域向前推进一步,状态变量也会通过状态转移方程（18）向前推移,再对目标函数J进行优化得到k+1时刻的控制序列,重复上面的过程。

3 仿真结果分析

运用后向仿真的方法建立的PHHV模型，模型输入选取美国城市道路循环工况（UDDS）。因为该工况含有频繁的起停和急加/减速工况，并且怠速时间短，非常利于客观评价PHHV在行驶过程中对能量的回收再利用情况。UDDS工况历时1 360 s，路程11 957 m，具体工况图如图8所示。

为满足循环工况每一时刻的速度需求,车辆动力系统和制动系统所应提供的总需求功率如图9所示。结合图8和9可以看到，在循环工况中，速度增加时需求功率为正,表示需要动力源提供车辆加速的动力；速度减少时需求功率为负，表示需要制动，由制动系统提供车辆减速的制动力。图10为行驶过程中，车辆累积的驱动能量和制动能量，工况结束时驱动能量总计需要3.279×107J，制动能量总计需要1.457×107J。若能充分回收利用制动能量，可以有效降低燃油消耗，提高燃油经济性。若能通过合理的能量管理策略来分配管理PHHV中液压能的使用则能提高制动能量的利用率，间接节省燃油提高燃油经济性。

利用建立的PHHV后向模型，设置好模型相关参数，运用MPC控制器来进行动力源的能量分配。由于1 100～1 150 s时间段需求功率分配的情况曲线更典型清晰，故选此典型时间段研究MPC能量管理策略的作用，如图11、12。

（1）车辆从1 102 s开始进入加速阶段，直至1 108 s左右，MPC很好的控制了发动机和泵马达共同给车辆提供驱动能量，此时由于蓄能器对外输出了能量，SOC从0.6左右下降到0.55。

（2）1 108~1 116 s时间段，车速继续上升，在MPC控制作用下，蓄能器停止输出能量，SOC保持不变，由发动机单独提供车辆前进动力。

（3）1 116～1 137 s时间段，车辆缓慢加速。基本上全部由蓄能器提供驱动能量，SOC迅速下降至0.1。

（4）1 137～1 140 s时间段，由于蓄能器能量已达到阈值下限，暂时由发动机作为动力源驱动车辆前进。

（5）1 140～1 150 s时间段，车辆开始减速，发动机停止工作，泵/马达工作在泵状态，给蓄能器充能，SOC从0.1开始上升。

从1 100～1 150 s车辆运行的情况可以看到MPC较好的实现了动力源能量的分配。

在整个工况中，能量的分配情况如图13所示。图13是MPC对车辆行驶过程中的需求能量进行实时分配的情况，可以看到MPC在车辆行驶过程中合理分配了发动机和液压单元的需求能量，共同驱动车辆前进。图14为蓄能器所存储能量的变化情况，由于工况前21 s为停车状态，SOC一直保持为0.9，即阈值上限。随后车辆进入急加速阶段，蓄能器和发动机共同提供能量，SOC值开始下降。

为了对比研究传统车辆、基于规则能量管理的PHHV和基于MPC能量管理的PHHV三种情况下的燃油经济性，选取曲线清晰的典型时间段820～880 s研究其燃油质量流量情况，如图15所示。

在824～832 s，841~850 s，870~874s时间段，通过规则管理能较好的降低车辆消耗的能量，MPC在上述时间段相比规则法更进一步降低了油耗。特别是在830 s前后和850 s前后，MPC能量管理的节油效果尤其明显。

表2为三种情况下的累积消耗燃油情况的比较，行驶结束时规则法累积消耗燃油2.242 L,相比传统车辆燃油经济性提高18.4%，MPC法消耗燃油2.054 L,相比传统车辆燃油性提高25.3%。表明MPC控制策略能有效的提高混合动力车辆的能量管理效率，节省燃油。

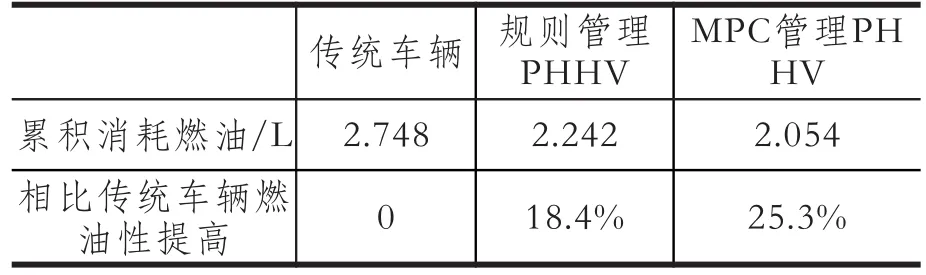
表2 燃油经济性比较

4 结论

能量管理策略关系到混合动力车辆的多个动力源能否协调工作，达到节能减排的效果。本文建立了PHHV的后向仿真模型，以蓄能器荷电状态（SOC）和发动机瞬时燃油质量流量为输入量,发动机需求功率比例φ为输出量，设计了模型预测控制器（MPC）进行PHHV的能量管理。仿真结果表明相比规则法，MPC管理策略在PHHV车辆行驶过程中合理分配了发动机和液压单元的需求功率，发挥了混合动力技术节能的优势，有效提高了燃油性。

[1]H.Murrehnolf, E.Weishaupt.Recent Developments for the Control of variable Displacement Motors with Impressed Pressure [J].Third JHPS International Symposium on fluid Power.Tokyo, 1996:79~84,68.

[2]Delprat Sebastian.Control Strategy Optimization for a Hybrid Parallel Power Train[J].Proceedings of the American Control Conference, 2001:25~27.

[3]Mark George Kosowski, Prekash H.Desai.A parallel hybrid traction system for General Motors Corporation’s“Precept” PNGV vehicle[C].SAE 2000-01-1534,2000.

[4]E.D.Mark.The Evaluation and Analysis of a Power Split Hydraulic Hybrid Drive train[J].Thesis on Master of University of Missouri-Columbia, 2003:30~50.

[5]Paganelli G, Ercole G, Brahma A, et al.General supervisory control policy for the energy optimization of charge-sustaining hybrid electric vehicles[J], Special Issue of JSAE Review, 2001,22(4):511~518.

[6]彭涛,陈全世.并联混合动力电动汽车的模糊能量管理策略[J],中国机械工程，2003，14(9):797～800.

[7]L.B.Karen, E.Mehrdad, K.Preyas.Matlab-based Modeling and Simulation Package for Electric and Hybrid Electric Vehicle Design[J].IEEE Transaction on Vehiculer Technology.1999,48(6):1770~1778.

[8]钱耀义,吴鑫铭,蒋和.柴油机的机械损失[J].汽车技术,1987,(02)

[9]Power Management Strategy for A Parallel Hybrid Electric Truck[J].10th Mediterranean Conference on Control and Automation.2002.

[10]Hans Joachim Ferreau, Peter Ortner, Peter Langthaler et al.Predictive control of a real-world Diesel engine using an extended online active set strategy[J].Annual Reviews in Control.2007,31:293~301.

[11]Maria Karlsson, Kent Ekholm et al.Multiple-Input Multiple-Output Model Predictive Control of a Diesel Engine.6th IFAC Symposium Advances in Automotive Control ,2010.

专家推荐

何华强：

本文简要介绍了液压混合动力的工作原理及关键总成的物理建模，着重介绍了基于UDDS工况，采用MPC的控制策略对系统进行最佳的控制，达到了节能的目的。目前新能源汽车开发以油电混合为主，液压混合动力从成本、可靠性、安全性而言有一定的优势，因此对于其核心的控制技术的研究具有积极的意义。

Reasearch on Strategy of Energy Management for Hydraulic Hybrid Vehicle Based on MPC

LI Ding-gen, YAN Suo, GAO You-min, MIAO Chun-hua
(1.Huazhong University of Science and Technology, Wuhan 430074, China; 2.Xiangfan Yuqing EV Co., LTD, Xiangyang 441021, China.)

Based on the model predictive control (MPC) theory, design the MPC controller for biaxial parallel hydraulic hybrid vehicles (PHHV).Its inputs are the accumulator charge state SOC and instantaneous engine fuel mass flow rate , output is the engine power demand proportion φ, the objective function is the minimum fuel consumption.BasedMATLAB/Simulink platform, establish PHHV backward simulation model including calculation model of power demand, transmission model, engine model, accumulator and hydraulic pump/motor model etc.The simulation results show that: PHHV can fully exert the characteristics of the hybrid based on MPC, distribute the demand power of ICE and hydraulic unit, reduce total fuel consumption in the UDDS driving cycle process.

Hydraulic Hybrid (PHHV); energy management; Model Predictive Control(MPC)

TP273

A

1005-2550（2014）05-0001-07

10.3969/j.issn.1005-2550.2014.05.001

2014-02-15

国家863项目资助（2012AA111102）。