储罐底板阴极保护电流密度分布规律研究

姜 旭

(中国石油西南管道公司兰州输油气分公司，甘肃 兰州 730060)

0 引言

平均保护电流密度是储罐底板阴极保护工程设计中重要的评价参数，目前我国对储罐保护电流密度尚无规定，国外对保护电流密度的规定也不统一，德国选取5mA/m2，日本选取6mA/m2，英国选取10mA/m2。大量资料证明，保护电流密度为10mA/m2是可取的，对于新建储罐，该指标可能偏高，后期比较适中，根据我国实际工程经验，选择5～10mA/m2是比较适宜的[1]。

使用有限元、有限差分、边界元等数值方法是研究阴极保护体系保护电位分布问题的发展方向，本文根据两种典型电流密度分布假设求解保护电位，建立了一个实际深井阳极储罐底板阴极保护体系的数学模型，将数值计算结果和实测数据进行了对比，并评价了两种电流密度假设的优劣性，对于新建阴极保护工程设计具有一定的指导意义。

1 数学模型

稳态分布型阴极保护体系电位分布满足Laplace方程[2,3]：

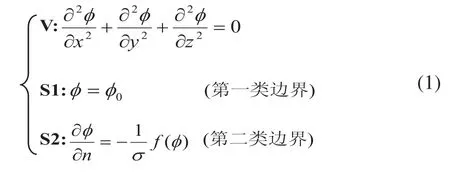
式中S1:辅助阳极，S2:被保护金属表面，σ:区域内介质电导率，)(φf:被保护金属表面极化电流密度。

2 边界条件

(1)辅助阳极

本文根据文献[4]中提供的方法近似计算辅助阳极电位:①根据选择的平均电流密度和储罐面积试算所需的保护电流I0；②计算罐底板接地电阻；③计算阳极电缆电阻RW；④计算阳极接地电阻R；⑤计算回路总电阻；⑥计算理论恒电位仪输出电压U'；⑦根据恒电位仪的型号和U'的大小选择实际恒电位仪输出电压U，利用欧姆定律得到阳极电位近似值。

(2)计算区域边缘

距离阳极较远时，电位变化很小(等于金属在土壤中的自然电位，即受阳极影响很小)，计算区域边缘的电位梯度等于零：

(3)储罐

①电流密度假设Ⅰ

文献[5]根据静电学原理推导圆盘电流密度i公式：

式中i:圆盘导体距圆心a点的电流密度mA/m2，a:该点距圆中心的距离m，r:圆盘半径m，I:圆盘总电流A，SiIs×=，si:平均电流密度mA/m2，S:储罐面积m2。

②电流密度假设Ⅱ

文献[6]指出罐底电流密度i是距罐底中心距离y的函数：

式中r:罐底半径m，k:反映罐底电流密度不均匀性的经验常数，等于30，i0:罐中心电流密度mA/m2，可证明：

3 计算实例Ⅰ

(1)假设条件

假设：①计算区域分成土壤介质和沥青砂基础两部分，在单独的区域中是均匀各向同性的；②金属结构表面状态不发生变化，保护电位不随时间发生变化；③不考虑杂散电流影响；④辅助阳极表面是等电位面，不考虑阳极表面电位随电流密度的非线性变化造成的阳极极化。

(2)计算参数[7]

土壤电阻率:5Ω·m；储罐沥青砂基础电阻率:200Ω·m。土壤和金属材料参数见表1和表2。

表1 土壤参数

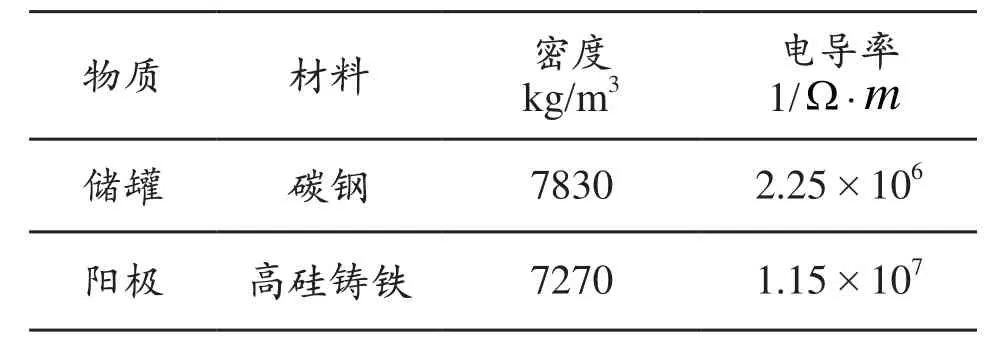
表2 金属材料参数

(3)阴极保护参数

金属自然腐蚀电位：-0.55V，最低阴极保护电位：-0.85V，最高阴极保护电位：-1.2V，储罐底板平均电流密度：6mA/m2。

(4)几何模型

储罐MN和单支深井阳极B，直径40m，底板厚度12mm，深井阳极YJB3SiCr-75×1000(15组)，阳极距储罐边缘30m，埋深40m，见图1。在储罐底板选取特殊点，小圆直径为大圆直径一半，相邻直线夹角45°，见图2。

图1 深井阳极示意图

图2 储罐底板特殊点分布图

考虑到电位分布对称性，两种电流密度假设对应的储罐底板水平轴线A7A3、垂直轴线A1A5和斜对角线A2A6/A4A8保护电位分布见图3、图4、图5，特殊点电位见表3。

表3 两种电流密度假设对应的电位对比结果

图3 水平轴线A7 A3保护电位分布

图4 垂直轴线A1 A5保护电位分布

图5 斜对角线A2 A6 /A4 A8保护电位分布

4 结论

(1) 两种电流密度假设对应的保护电位分布规律相似，距离阳极越近，电位越高，反之电位越低，两种保护电位相对误差小于5%。

(2) 电流密度假设Ⅱ对应的保护电位在近阳极端和远阳极端出现两个极值；电流密度假设Ⅰ对应的保护电位仅在远阳极端出现极值，若评价两种方法的优劣，需要现场实测数据验证。

5 计算实例Ⅱ

(1)几何模型

文献提供了使用多孔PVC参比电极测量实际罐底板保护电位分布的数据，储罐直径36m，罐边缘到罐中心径向方向等距测量13个点，is≈6mA/m2，深井阳极距离储罐较远，具体数据不详，数值计算中设定为52m，埋深30m，长度15m。数值结果与电位实测数据对比见表4。

(2)结果分析

数值结果与电位实测数据相差不大，近阳极端储罐边缘区域内电位结果相差较大，这主要是两方面原因造成的：

①阴极保护电位准则范围不同，一些情况下(含硫酸盐或还原性细菌土壤中)工程实际最大阴极保护电位允许达到-1.5V，本文阴极保护电位范围是-0.85～-1.2V；

②工程实际中深井阳极极化电位是动态变化的，本文根据阴极保护系统参数近似计算辅助阳极极化电位(等于常数)。

(3)结论

①电流密度假设Ⅰ对应的保护电位在0.5r～r(r储罐半径)范围内与实测电位数据吻合较好，电流密度假设Ⅱ对应的保护电位在0～0.5r范围内与实测电位数据吻合较好；

②对比结果验证了数值方法的可靠性，从整体上考虑，使用电流密度假设Ⅰ可以较好的模拟储罐底板阴极保护体系。

表4 数值结果与电位实测数据对比

6 结束语

目前储罐阴极保护工程设计中是根据被保护面积和选择的平均电流密度计算所需的保护电流，进而对恒电位仪进行选型，根据数值计算结果，选择电流密度假设Ⅰ和合适的平均电流密度可以初步了解储罐底板的电流密度分布情况；应该指出，式(4)中，当ra→，∞→i，根据电流密度的有限性原则，这与实际是不相符的，这也是该模型存在的缺陷，建立更加完善的保护电流密度分布模型是储罐底板阴极保护技术的研究方向。

[1]王维. 钢质储罐罐底外壁阴极保护设计[J]. 石油规划设计, 1997,12(1):21-22.

[2]邱枫, 徐乃欣. 钢质储罐底板外侧阴极保护时的电位分布[J]. 中国腐蚀与防护学报, 1996, 16(2):29-35.

[3]翁永基. 阴极保护设计中的模型研究及其应用[J]. 腐蚀科学与防护技术, 1999, 11(2):99-111.

[4]胡士信. 阴极保护工程手册[M]. 北京化学工业出版社, 1999.122-127.

[5]俞蓉蓉, 蔡志章. 地下金属管道的腐蚀与防护[M]. 北京:石油工业出版社, 1998.223.

[6]李相怡, 翁永基. 金属储罐底板外侧阴极保护电位分布的解析计算法[J]. 石油学报, 1998, 19(7):98-103.

[7]李章亚, 张清玉. 油气田腐蚀与防护技术手册[M].石油工业出版社, 1998. 254.