呼吸墙阻抗-动态流量计算模型

赵 越 张腾飞 王树刚

大连理工大学建设工程学部

呼吸墙阻抗-动态流量计算模型

赵 越 张腾飞 王树刚

大连理工大学建设工程学部

呼吸墙作为一种新型的建筑室内引风方式得到了广泛关注，其诱导的通风量受风压与热压共同作用决定。为了获得在风压与热压作用下的呼吸墙阻抗与流量特性关系，通过理论关联式分析方法建立了简便的呼吸墙计算模型，并应用计算流体力学（CFD）对呼吸墙进行了建模仿真，将两类模型的计算结果与实验测试结果进行比较。文中还分析比较了不同辐射热量、风压及多孔填料厚度下，呼吸墙通流阻力及通风量的变化关系。结果表明，关联式与CFD计算模型具有较好精度，可用于不同结构参数的呼吸墙设计。

呼吸墙阻抗-流量理论计算模型实验测试

0 引言

作为一种新型的建筑室内引风方式，呼吸墙具有良好的应用前景。由于呼吸墙可内置多孔过滤材料，可实现在引入室外新风的同时阻隔室外噪音，并对引风进行过滤净化，非常适用于改善闹市区的各类建筑室内环境。要设计好呼吸墙，须弄清楚呼吸墙的阻抗-流量特性、保温性能及空气过滤效果。本文首先探讨呼吸墙的阻抗-流量特性。

呼吸墙诱导的通风量取决于热压、风压以及系统结构阻抗等因素。有关求解呼吸墙通风量方法主要有三种：理论关联式法、CFD数值模拟及实验测试法[1]。关联式法基于压力平衡方程，热压与风压共同作用时，呼吸墙承受的总压可以叠加，但其通风量却不再是热压与风压单独作用下的通风量之和[2]。理论关联式法在竖直流道通风量预测的研究中被大量应用，尤其以太阳能烟囱最为广泛。在热压的作用下，流道内通风量可以通过关联式求解[3]，但耦合风压共同作用下的理论关联式还不多见。此外，太阳能烟囱相较呼吸墙结构简单，无迂回流道和过滤单元，与之对应的理论关联式应用范围较为局限。近年来，计算流体力学（CFD）方法逐步被应用到呼吸墙通风量的预测上。Awbi和Gan提出应用标准k-ε湍流模型及Boussinesq假设计算太阳能烟囱通风量。其计算结果[4]与Bouchair的实验结果[5]相近，但仅就浮升力作用产生的热压工况进行了探讨。Moshfegh和Sandberg针对空腔内气流形式及通风量等信息进行了模拟分析[6]，同样未对风压、热压耦合作用的效果进行探究。实验测试法可为呼吸墙的运行性能提供较为全面的评估，且可得到呼吸墙内部各局部及沿程阻力损失系数进而求得阻抗系数[7]。同时，可为理论关联式法和CFD数值模拟法的结果提供验证。

上述研究中，所运用的理论关联式模型适用结构均比较简单，无法满足呼吸墙的迂回流道设计。呼吸墙增设多孔过滤单元，使得系统阻抗与流量关系更加复杂，简单的关联式模型计算精度得不到保证。而CFD数值模拟的方法多数针对某单一压差作用下的空腔流量进行预测，缺少了风压与热压耦合作用下的研究。本文从自然通风的机理出发，利用理论分析的方法推导阻抗、流量以及各参数间的关系，得到理论关联式，可针对多种呼吸墙结构的通风量进行预测；并应用CFD数值模拟探究呼吸墙在热压和风压耦合作用下的性能参数；通过实验测试的方法对上述研究结果进行了验证。

图1 呼吸墙系统示意图

1 研究对象

图1（a）给出一种呼吸墙结构，详见参考文献[8]。呼吸墙接收阳光照射，辐射吸收板加热空腔内部空气，产生浮升力驱动空气流动，即所谓的热压驱动；另一方面，室外风压同样可以将空气压入呼吸墙空气流道内，形成风压驱动。进入墙体内的空气经过滤单元的洁净处理，最终被送入室内环境。当热压和风压耦合作用于呼吸墙时，需满足压力动态平衡方程，即系统运行时的全压损失等于热压和风压代数和。呼吸墙结构确定时，其固有的阻抗系数也随之确定。图1（b）中，呼吸墙空腔辐射吸收板高度为H，空气过滤单元高度为ΔL。呼吸墙的压力损失主要包括空气进出口及各弯头的局部阻力损失、空气沿流道内的沿程阻力损失以及空气流经过滤单元的压降损失。

2 研究方法

本文采用了理论关联式分析、CFD数值计算以及实验测试相结合的研究方法。

2.1 关联式模型

呼吸墙的气流通道包括进出口、迂回流道及过滤单元，将气流通道视为流体管路进行分析，则该管路下存在固有阻抗值。系统总压差ΔPt(V)、体积流量V与阻抗ψ的关系满足：

其中，阻抗值与呼吸墙的结构参数有关，其表达式为：

式中：等式右边第一项表示沿程阻力损失，λi为沿程阻力系数；Li为流道长度，m；Def为流量当量直径，m；Ai为流道截面积，m2。第二项为局部阻力损失，ξj为局部阻力系数；Aj为局部出口截面积。第三项则为过滤单元压降损失，Cpm为多孔介质沿程压降损失系数，m-1；φ为多孔介质孔隙率；Apm为多孔介质区域截面积；ΔL为多孔填料厚度；ρ为空气密度，kg/m3。

1）热压-流量方程

空气在呼吸墙玻璃板与辐射吸收板之间的空腔内部存在温度分层，形成密度差，沿着呼吸墙壁面的垂直方向出现压力梯度，进而形成热压差，其原理等同于“烟囱效应”。热压的大小取决于高度差和空腔内部的空气密度差，基于热量平衡方程与压力平衡方程求解诱导流量[3]。热压单独作用时，呼吸墙诱导通风量与辐射热量之间的关系表达式：

其中w是与呼吸墙空腔高度（H）与宽度（w）、辐射热量（q''）以及浮升力系数B有关，定义为：

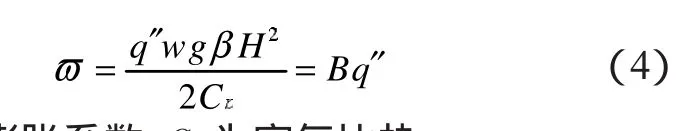
式中：β为气体膨胀系数，Cp为空气比热。

而辐射热量与热压差ΔPb(V)之间的关系满足：

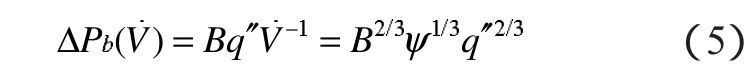
由式（3）和（5），可分别求得在任意辐射热量下的空气流量及对应压力损失。

2）风压-流量方程

风压受室外风速及地形参数等因素影响。本文不关注瞬态风引起的气流变化形式，而将风压作为给定值用以平衡系统压力损失。风压差与流量之间的关系满足：

其中，ΔPw(V)表示风压差，其值等于空气流经呼吸墙流道及过滤单元的各局部阻力和沿程阻力损失之和。由式（6）即可求得在任意室外风压差下的诱导空气流量。

3）热压风压-流量方程

热压与风压往往是共同作用的。此时呼吸墙的作用压头等于二者的代数和，但其诱导通风量不等于两者各自通风量的线性叠加。若要求得通风量，就要从平衡压力损失入手，即系统全压损失ΔPt(V)等于热压差ΔPb(V)和风压差ΔPw(V)之和，表达式如下：

本文假定呼吸墙进出口的风压值为均一恒定值，则ΔPw(V)=ΔPw，即风压差不再是通风量的函数。而热压值仍与通风量有关。将式（1）、（5）代入式（7）中，转化为：

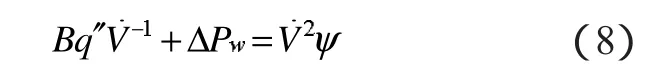
上述公式，即为热压风压共同作用下的诱导通风量关系式，写成函数关系为：

由式（9）可见，呼吸墙通风量主要受浮升力系数、阻抗、辐射热量以及风压差影响。前两者为呼吸墙内部参数，后二者为外部参数。呼吸墙结构确定后，内部参数随之确定，进而利用该理论计算模型即可求解不同外部参数下的诱导通风量。

2.2 CFD数值模拟

为了获得更为详细的有关呼吸墙阻抗-流量间特性参数信息，同时与理论关联式模型的结果加以对比分析，本研究还使用了CFD方法对呼吸墙在不同风压、热压运行下的性能参数开展了数值模拟。模拟中，由于温差的变化引起浮升力的问题，故而引入Boussinesq假设。假设由以下几部分组成：1）流体中的粘性耗散忽略不计；2）除密度外其它物性为常数；3）对密度仅考虑与体积力有关的项，其余各项中的密度亦作为常数。

过滤单元内部的细节流动并不是本文主要关心的内容，所以将过滤单元结构假定为某种多孔介质，把空气在过滤单元内部的流动看成是多孔介质内的流体运动。计算过程中，将粘性阻力和惯性阻力作为边界条件给出，再给定孔隙率，流体通过多孔介质的流动便可近似计算[9]。

参照图1（b）中模型的形式，建立如图2所示的数值几何模型。进排风口高度为0.1m，空腔内部宽度为0.08m，呼吸墙高度为1.3m，加热板高度为1.12m，多孔介质区域高度作为自定义变量定义为ΔL，设计高度分别为3cm、6cm以及10cm。具体CFD模拟边界条件设计如表1。其余壁面做绝热处理，模拟中多孔介质区域的颗粒当量直径为2.8mm，孔隙率为0.48。

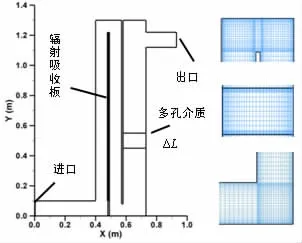
图2 呼吸墙CFD几何模型及局部加密网格

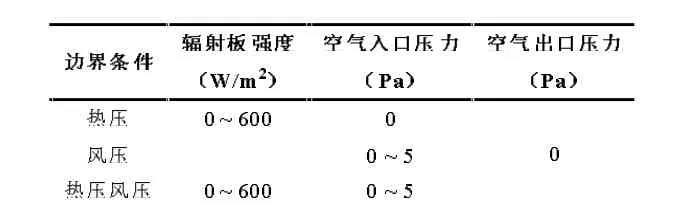
表1 CFD模拟边界条件

应用前处理软件GAMBIT(2.3.16)建立如图2所示的几何模型，通过“Map”方案生成结构化矩形网格，总网格数量分别为25359、25547和25765。因为在空腔近壁面处速度梯度较大，为获得层流底层内精确的速度分布并减少网格的使用总量，采用渐变尺寸网格，确保第一层网格的y+<5，局部加密网格如图2所示。靠近壁面处网格厚度最小值为0.4mm，然后按1.1的增长率由两侧壁面朝中心增大网格间距，流道中心区域沿流道宽度方向上的最大网格间距为4mm。

数值模拟计算中，选用RNG k-ε湍流模型并且应用增强型壁面函数法来近似壁面效应[4，6，10]。能量方程、动量方程、湍流动能和湍流耗散率均采用二阶迎风差分格式。连续性与动量方程的耦合选用SIMPLE算法。质量、速度、湍流动能及湍流耗散率的收敛判据为迭代误差小于10-5，能量小于10-6。

2.3 实验装置测试

本文建立了呼吸墙实验测试装置，为理论分析以及CFD数值模拟提供了实测依据，从而验证本文模型的实用性。

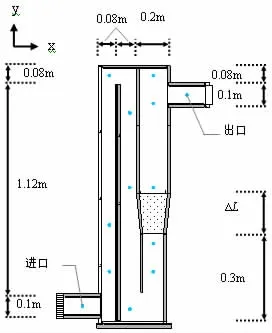
图3 呼吸墙实验测试示意图及测点分布

呼吸墙实验模型如图3所示，其具体尺寸与CFD数值模拟模型一致。过滤材料使用石英砂（主要成分SiO2），平均粒径2.8mm，孔隙率约为0.48（同CFD模拟条件）。根据CFD模型工况的设定，实验中将石英砂分为3cm、6cm和10cm三个填充高度。太阳能辐射吸收板表面的辐射热量由云母加热板提供。实验中，将加热板与变压器连接，通过改变输入电压调节加热板实际的热量输出值。经测试，云母加热板的电阻值为53Ω。使用不同型号直流风机满足风压需求，利用风机频率、转速等信息，估算实际提供压头，进而改变工况，满足验证需要。详细实验工况情况见表2。

表2 实验测试工况及边界条件

实验中，加热板发热量由输入电压换算求得，其对应关系如表3。

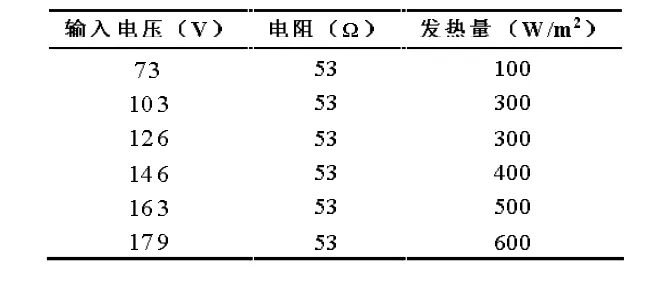
表3 云母加热板输入电压与发热量关系

恒定加热源产生的热压通风，空腔内的空气流动呈现脉动规律[1]。测试过程中，需要精度较高稳定性较强测压仪器。本实验中，使用TSI高精度微压计（型号：8715）对各节点压力值进行了测定，分辨率为0.001Pa，精度为±2%读数±0.025Pa，从而满足实验要求。

3 对比结果分析

3.1 风压独立作用下压差流量特性

本文首先对风压独立作用下的呼吸墙阻抗-流量特性进行了分析，如图4所示。图中的压力值代表呼吸墙进气口与排气口两个高度上的全压差，作为克服系统阻力提供空气流动的驱动力。

图4风压与流量关系结果对比分析

图4 给出了理论特性曲线、CFD模拟与实验测试结果。从图中可以直观地看出，相同风压作用下，多孔填料厚度越小，呼吸墙诱导的流量越大。实验装置墙体存在接口缝隙以及仪器误差等客观因素，实验测试结果普遍低于模拟与理论计算值，但误差均小于10%。由结果对比分析可见，风压作用下理论预测关联式及CFD数值模型基本可以满足对于呼吸墙通风量的预测要求。

3.2 热压独立作用下压差流量特性

图5给出了不同过滤单元高度结构下，呼吸墙由热压独立作用时的阻抗-流量特性关系。

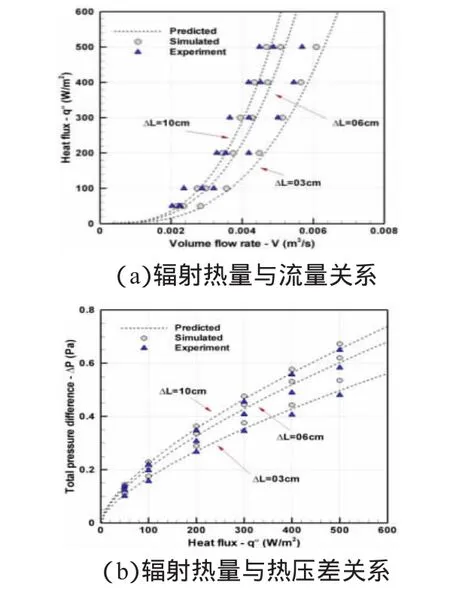
图5 热压与流量关系结果对比分析

图5（a）给出了加热密度与空气流量之间的关系，可以看出加热板热流密度相同时，呼吸墙诱导流量同样随着多孔填料厚度的减小而增大。太阳日照辐射热量最大时可达800～1000W/m2，考虑实际应用时呼吸墙辐射吸收板接收日照辐射的能力，本文只对0～500W/m2区间内工况进行了模拟和测试。从对比结果可以看出，模拟值略小于理论值。模拟时，呼吸墙出口存在倒流现象，从而使得通风量变小，但其影响随着加热板热流密度的增加而逐渐降低。实验值仍小于模拟值与理论值，这同样可能是由于实验装置的密闭性影响；同时，热压作用时，呼吸墙内部气流呈脉动方式流动，所以在测试时需要对每一测点进行长时间的监测，加之实验仪器存在误差，所以实验值较小，但偏差仍在仪器测试误差允许区间内。

不同热流密度下，呼吸墙产生的热压差随之变化，该热压差值与风压值相比较小，范围在0～1Pa之间，如图5（b）所示。

结合图5（a）和（b），以ΔL=10cm为例，在加热密度为400W/m2时，呼吸墙诱导得到的空气流量约为0.0045m3/s，对应热压差为0.563Pa。虽然热压诱导下的通风量有限，但其作用下的呼吸墙结构可以成为理想的保温介质，室外冷空气可以被加热成温度适宜的洁净温暖空气被输送到室内空间，降低了室内供暖下的热负荷，同时改善了室内空气品质[11]。

3.3 热压、风压耦合作用下压差流量特性

热压、风压共同作用下时，呼吸墙的综合压差等于二者的代数和，二者同向时，可增强自然通风；二者反向时，则削弱自然通风。本文旨在探究呼吸墙在二者综合作用下诱导通风量的最大潜力，所以只针对二者同向工况进行研究。

通过理论分析的方法得到了空气流量与热压日照辐射热量以及风压差之间的求解函数：V=f(q'',ΔPw)，三者的关系可以运用三维曲线表示，但是为了简便清晰地理解三者之间的关系，本文选取两种特定工况对其进行研究：1）热压值不变（400W/m2），风压值变化；2）风压值不变（1Pa），热压值变化。

图6（a）给出了当热压值不变时（辐射热量恒为400W/m2），呼吸墙流量与风压差之间的关系。从图中可以看出，当风压值为0时，流量值等于辐射热量为400W/m2时产生的诱导流量。随着风压差的小幅增加，空气流量逐渐增加，但值接近热压对应下的流量值。同样以ΔL=10cm为例，当风压差约为0.5Pa时，此时的诱导流量为0.006m3/s，约为风压独立作用时（0.0042m3/s）的142%，可以看出，热压对于通风量有增益作用，提升了约42%的通风量。当风压差为3Pa时，此时的诱导流量为0.011m3/s，约为风压独立作用时（0.0097m3/s）的113%，可见在该工况下，热压对于通风量的增益效果比较小，空气流量主要受风压作用。

图6（b）为风压值为1Pa时，辐射热量与流量的关系。辐射热量为0时，空气流量等于风压为1Pa的诱导流量。随着热量的增加，呼吸墙诱导的空气流量虽然逐渐增加，但增加幅度很小。风压约为1Pa时，流量的大小主要受风压的影响，热压值的大小对流量仅有较小影响，主要的效果则用于对该流量下的空气进行加热，传热特性方面影响提升。实验与模拟值均小于理论计算值，但整体趋势相似，误差较小，吻合度较高。

图6 热压风压与流量关系结果对比分析

4 结论

本文应用理论关联式分析、CFD模拟及实验测试的方法研究了呼吸墙在热压风压耦合作用下的阻抗与流量的特性关系。其结论如下：

1）理论关联式分析和CFD模拟方法分别求得了呼吸墙在热压、风压单独作用及二者共同作用下系统总阻力与流量特性，与实验测试结果对比表明这两类模型均具有较好精度，但关联式分析计算效率更高。

2）理论关联式分析与CFD计算模型均可对不同内部结构参数及外界环境参数的呼吸墙系统的诱导通风量进行有效预估，亦可对呼吸墙系统提供优化设计方案及运行策略指导。

[1]谭刚,朱颖心,李晓锋.热压自然通风的实验研究与数值模拟[A].见:全国暖通空调制冷2000年学术年会论文集[C],长沙, 2000,921-924

[2]Li YG,Delsante A.Natural ventilation induced by combined wind and thermal forces[J].Building and Environment,2001,36 (1):59-71

[3]Chen ZD,Bandopadhayay P,Halldorsson J,etal.An experimental investigation of a solar chimneymodelwith uniform wallheat flux[J].Building and Environment,2003,38(7):893-906

[4]Awbi HB,Gan G.Simulation of solar-induced ventilation[J]. Renewable Energy Technology and the Environment,1992,4: 16-30

[5]Bouchair A.Solar chimney for promoting cooling ventilation in southern Algeria[J].Building Service Engineering,Research and Technology,1994,15(2):81-93

[6]Moshfegh B,Sandberg M.Flow and heat transfer in the air gap behind photovoltaic panels[J].Renewableand Sustainable Energ -y Reviews,1998,2(3):287-301

[7]Rodrigues AM,de Piedade AC,AwbiHB.The use of solar air collectors for room ventilation:A study using two numerical approaches[C].In:Proceeding of 7th International Conference on Air Distribution in Rooms(Roomvent2000),1:281-288

[8]张腾飞,赵越,王树刚,等.一种节能环保型多功能呼吸墙[P].国家知识产权局,2010

[9]陈威,刘伟.多孔介质太阳能集热组合墙的耦合传热与流动分析[J].太阳能学报,2008,29(2):220-227

[10]YakhotV,Orzag S,Thangam S,etal.Developmentof turbulence models forshear flowsby adoubleexpansion technique[J].Phys -icsof Fluids(A),1992,4(7):1510-1520

[11]Zhao Y,Zhang T,Wang S,etal.An activebreathingwall to impr -ove indoorenvironment[C].In:Proceedingsof Building Simula -tion 2011:12th Conferenceof InternationalBuilding Performance Simulation Association,2011,429-435

Pre d ic tion o f Flow Re s is tan c e Ve rsu s A irflow Ra te in a B rea th ing W a ll

ZHAO Yue,ZHANG Teng-fei,WANG Shu-gang
Faculty of Infrastructure Engineering,Dalian University of Technology

As a novelmode to intake outdoor air for room ventilation,breathing walls have been attracted significant concerns.Theairflow rate induced by a breathingwalldependson both the thermaland thew ind pressure.To obtain the causalquantitative relation between flow resistance and airflow rate,this investigation established two setofmodels in termsof theoretical correlation analysisand Computational Fluid Dynamics(CFD).Bothmodels can take into account various conditions,such as,different radiation incidence,w ind pressure and porous filtration thickness.In addition, experimental tests were also conducted to obtain data to validate both types of models.The results show that the correlation model can provide accurate results that are comparable w ith the CFD modeling but at much lower computationalcost.Therefore,bothmodels can be applied to aid the design of breathingwalls.

breathingwall,flow resistance vs.airflow rate,correlationmodel,measurement

1003-0344（2014）02-001-6

2013-4-18

张腾飞（1978～），男，博士，副教授；辽宁省大连市甘井子区凌工路2号大连理工大学实验四号楼437室（116024）；0411-84706279；E-mail:tzhang@dlut.edu.cn

国家自然科学基金（No:50978039）