无网格对称粒子法中两类热边界条件的处理

肖毅华，张浩锋，平学成

（华东交通大学机电工程学院，江西南昌330013）

无网格对称粒子法中两类热边界条件的处理

肖毅华，张浩锋，平学成

（华东交通大学机电工程学院，江西南昌330013）

第二、三类边界条件对无网格对称粒子法求解瞬态热传导问题的计算精度和稳定性有重要影响。提出一种有效的方法来处理这两类边界条件。该方法采用统一表达式描述两类边界条件，并将边界粒子分为光滑域内的边界粒子和非光滑域的边界粒子。对于前者，在温度导数的对称粒子近似中引入边界条件方程，精确地施加边界条件；对于后者，根据其相邻粒子的温度导数，采用具有一阶连续性的粒子近似，计算出其温度导数。应用该方法计算了一个数值算例。计算结果与解析解和有限元法的计算结果符合良好，且计算误差随时间呈下降趋势，说明该方法具有良好的精度和稳定性。

瞬态热传导；边界处理；无网格对称粒子法

热传导问题［1-2］普遍存在于机械、材料、土木等研究领域。由于实际热传导问题的复杂性，人们往往需要借助数值方法进行研究。常用的数值方法是基于网格的方法，如有限元法［1］、有限体积法［2］。无网格法发展较晚，目前在热传导问题中也得到了一定的应用［3-8］。相对于基于网格的方法，无网格法显示出一些优势。它不涉及网格，可以避免网格畸变，且无需复杂和耗时的网格划分等步骤。但是，多数无网格法需要复杂的数值积分和形函数计算，计算量大、效率低。无网格法中的粒子法，如光滑粒子法（SPH），以带有质量、密度等物理量的粒子模拟物体，并用配点法离散控制微分方程，无需数值积分，具有概念简单、程序实现容易、计算效率较高等优点。近年来，一些研究者［9-10］探讨了此类方法在热传导问题中的应用。由于无网格粒子法是配点型无网格法，该类方法对边界特别是导数边界的处理很敏感。因此，边界条件的处理是关于此类方法研究的一个热点［11］。在热传导问题中，第二、三类边界条件都是导数边界条件，其处理对于保证无网格粒子法的精度和稳定性具有重要意义。

1 无网格对称粒子法的基本方程

在求解瞬态热传导问题时，无网格对称粒子法采用一组粒子离散问题域。每个粒子携带密度ρ，质量m和温度T等物理量。物理量的导数通过对称粒子近似进行计算。为了得到某一物理量f的一阶导数的对称粒子近似，对于任意粒子i，在其邻域内定义如下误差项

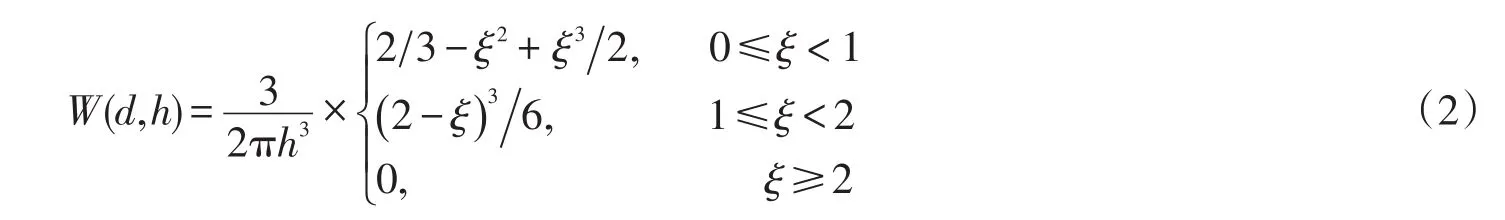
式中：ξ=d h；d为粒子间的距离；h为影响域半径。令式（1）定义的误差最小化并求解得到的线性方程组，即给出的对称粒子近似式为

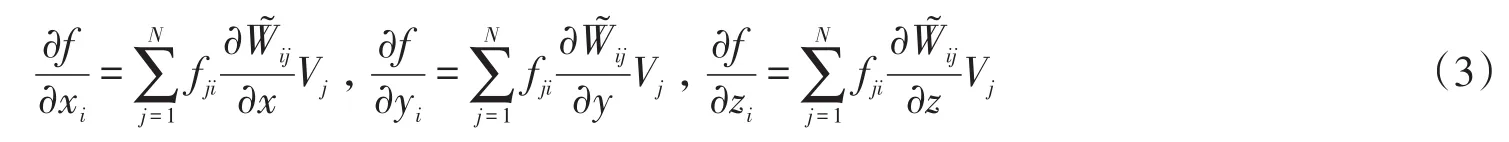
式中

利用式（3）对瞬态热传导问题的控制方程离散，得到无网格对称粒子法的基本方程为

式中：t为时间，c为比热，λx、λy和λz为3个坐标方向的导热系数，为热源强度。本文考虑各个方向的导热系数相同，即λx=λy=λz=λ。

2 边界条件处理

热传导问题涉及3类边界条件：第一类为给定边界上的温度值，第二类为给定边界上的热流密度分布，第三类为给定边界上物体与周围介质间的对流换热系数及介质温度。3类边界条件分别表述如下

式中：Ts为物体边界面上的温度，为给定的边界面上的温度分布函数；n为物体边界面的外法向量，为给定的边界面上的热流密度分布函数；α为对流换热系数，Ta为周围介质的温度。

对于第一类边界条件，无网格对称粒子法可以直接施加，即在每一时间步内将要满足此种边界条件的粒子赋予指定的温度值。第二类和第三类边界条件都包含导数，其处理相对比较困难。将这2种边界条件写为如下统一形式

式中：cosθx，cosθy和cosθz为边界面外法向量的方向余弦。

式（8）需要计算边界面外法向量的方向余弦，而外法向量在不光滑的边界位置（如图1所示）无法确定。因此，为了避免计算困难，本文将满足第二类和第三类边界条件的粒子分为两类：光滑域内的边界粒子为I类边界粒子，非光滑域的边界粒子为II类边界粒子。

对于I类边界粒子，根据边界条件方程式（8）易得

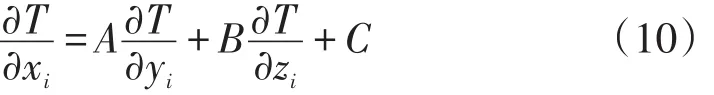
式中：A=-cosθyi/cosθxi，B=-cosθzi/cosθxi，C=κ/cosθxi。利用上式可将两粒子处的温度差近似表示为

图1 边界粒子的分类Fig.1 Classification of boundary particles

再将上式代入误差定义式（1）并令其最小化，求解得到

式中。根据上述过程求得的边界粒子的温度导数是精确满足边界条件的。值得指出的是，为了保证数值计算的稳定性，避免式（10）出现分母为0的情况，应选择将方向余弦绝对值最大的方向的温度导数用其余两个方向的温度导数表示出来。

对于II类边界粒子，先根据式（3）和式（10）、（12）分别计算完内部粒子和I类边界粒子的温度导数，再根据已计算出的粒子温度导数，通过具有一阶连续性的粒子近似计算得到其温度导数，计算表达式为

式中

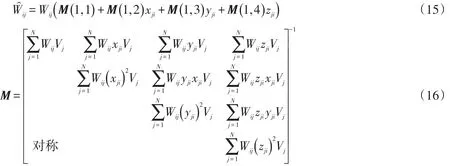
3 数值算例

下面通过一个数值算例来验证上节提出的边界处理算法的有效性。算例考虑边长为a=2的立方形物体在两种不同边界条件下的温度场变化。计算时采用无量纲化参数，物体的相关热物理参数为密度ρ=1；比热c=1；导热系数λx=λy=λz=1；物体的初始温度为1；热源强度=0。求解区域的原点设在其中心处，采用均匀分布的粒子对其离散；粒子间距为0.05，粒子总数为68 921；粒子的影响域半径为1.5倍粒子间距。模拟总时间设为0.2，计算时间步长取为0.001。

首先考虑在立方体表面作用第三类边界条件，即立方体的外表面与周围介质对流换热，设对流换热系数为α=1，周围介质温度为Ta=0。在此边界条件下，可以获得该问题的解析解［12］，从而便于检验算法的正确性和精度。图2给出了3个特征点A、B、C的温度变化历程，这3个点的坐标分别为（0，0，0）、（0.5，0.5，0.5）和（1.0，1.0，1.0）。可见，无网格对称粒子法计算的特征点温度与解析解在整个模拟时间段内都能良好地吻合。图3为时间t=0.2时立方体上表面（z=1.0）的温度等值线图。无网格对称粒子法计算的温度分布与解析解基本一致。

图2 第三类边界条件下3个特征点的温度变化Fig.2 Temperature histories of three representative points for boundary conditions of the third kind

图3 t=0.2时上表面（z=1.0）的温度分布对比Fig.3 Comparison of temperature distributions of the top surface（z=1.0）att=0.2

图4给出了无网格对称粒子法的计算结果与解析解的总体相对误差Re1和单个点最大相对误差Re2随时间的变化。两误差的定义分别为

式中：Tp(xi)和Tf(xi)为分别为根据粒子法和解析解计算的粒子点xi处的温度值，n为粒子数。由图4可见，总体相对误差始终小于1%，且随模拟时间的增加而减少；单个点的最大相对误差在开始时为8.4%，随后也呈递减趋势。以上结果说明了本文方法对于第三类边界条件具有良好的精度和稳定性。

图4 第三类边界条件下的总体相对误差和单个节点最大相对误差Fig.4 Relative error of the whole region and themaximum relative error at single points for boundary conditions of the third kind

下面考虑在立方体表面作用第二类边界条件的情况。设立方体各表面上都有均匀的热量输入，热流密度的大小为=1。在此边界条件下，难以得到解析解。为了验证边界处理算法的有效性，建立单元尺寸与粒子间距相同的有限元模型，以有限元法的求解结果作为参考依据，将无网格对称粒子法的结果与其对比。图5给出了与前述位置相同的3个特征点的温度变化历程。两种方法的计算结果在整个模拟时间段内也都符合良好。图6为两种方法计算结果的总体相对误差和单个节点最大相对误差的变化曲线。两种误差均随模拟时间的增加而减少，总体相对误差的最大值仅为0.6%，单个节点最大相对误差的最大值约为6%。以上结果可以说明本文方法对于第二类边界条件也是可行和准确的。

图5 第二类边界条件下三个特征点的温度变化Fig.5 Temperature histories of three representative points for boundary conditions of the second kind

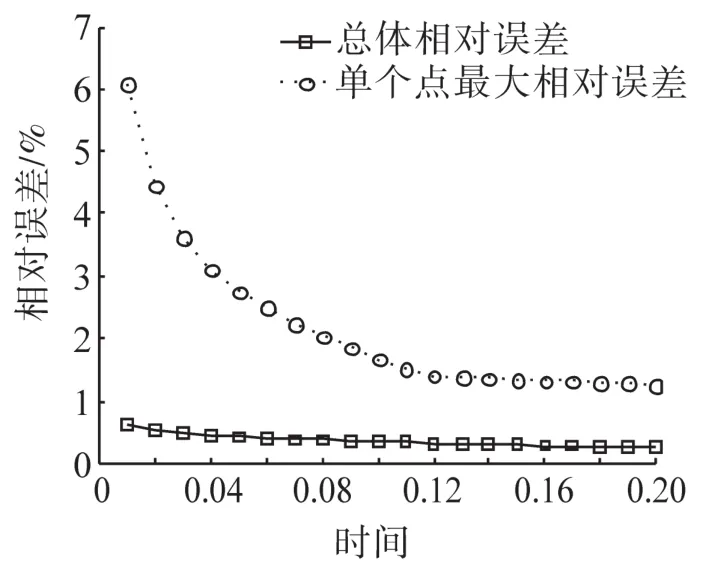
图6 第二类边界条件下的总体相对误差和单个节点最大相对误差Fig.6 Relative error of the whole region and themaximum relative error at single points for boundary conditions of the second kind

4 结论

研究了无网格对称粒子法求解瞬态热传导问题时第二类和第三类边界条件的处理，提出了一种统一的方法施加这两类边界条件。数值计算的结果表明该方法是十分有效的，能使无网格对称粒子法准确、稳定地求解具有第二类和第三类边界条件的瞬态热传导问题。同时，该方法无需添加辅助节点或在边界附近进行节点加密等，实施过程较简单，可以为无网格对称粒子法模拟复杂热边界条件提供了一种有效的途径，促进其在解决实际工程问题中的应用。

[1]倪昀,黄志超,熊国良,等.基于ANSYS汽车后桥壳体焊接温度场有限元分析[J].华东交通大学学报,2006,23(2):115-118.

[2]刘仍通,潘阳.自然对流影响结冰的数值模拟以及实验研究[J].华东交通大学学报,2010,27(5):22-27.

[3]王冰冰,高欣,段庆林.稳态热传导问题的二阶一致无网格法[J].应用数学与力学,2013,34(7):750-755.

[4]戴艳俊,吴学红,陶文铨.三维不规则区域热传导问题无网格方法的数值模拟[J].工程热物理学报,2011,32(7):1173-1177.

[5]吴学红,李增耀,申胜平,等.不规则区域热传导问题无网格Ptrov-Galerkin方法的数值模拟[J].工程热物理学报,2009,30(8): 1350-1352.

[6]SHIBAHARA M,ATLURI S N.Themeshless local Petrov-Galerkinmethod for the analysis of heat conduction due to amoving heat source,in welding[J].International Journal of Thermal Sciences,2011,50(6):984-992.

[7]CHENG R J,Ge H X.Meshless analysis of three-dimensional steady-state heat conduction problems[J].Chinese Physics B, 2010,19(9):090201-090201.

[8]蒋涛,欧阳洁,栗雪娟,等.瞬态热传导问题的一阶对称SPH方法模拟[J].物理学报,2011,60(9):090206-090206.

[9]章文捷,王小惠,江顺亮.瞬态热传导方程的SPH法[J].化学工程与装备,2010(10):18-23.

[10]金文佳,章文捷,王小惠,等.热传导问题的SPH方法及其边界处理[J].化学工程与装备,2011(10):37-41.

[11]张宏伟,李美香,李卫国.关于配点型无网格法边界条件处理技术[J].大连理工大学学报,2010,50(4):614-618.

[12]傅里叶.热的解析理论[M].北京:北京大学出版社,2008.

Treatment of Two Kinds of Thermal Boundary Conditions in Meshless Symmetric Particle Method

Xiao Yihua,Zhang Haofeng,Ping Xuecheng
(School of Mechatronics Engineering,East China Jiaotong University,Nanchang 330013,China)

Boundary conditions of the second and the third kind have important effects on the accuracy and stabili⁃ty ofmeshless symmetric particlemethod for the solution of transient heat conduction.An effectivemethod is pre⁃sented in this paper to treat boundary conditions of both kinds.Two kinds of boundary conditions are expressed in a uniform form,and boundary particles are divided into two categories,the particles in smooth boundary regions and particles in non-smooth boundary regions.For the former,boundary conditions are enforced exactly by consid⁃ering the equations of boundary conditions as constraints in the symmetric particle approximation of derivatives of temperature.For the later,their derivatives of temperature are approximated with a particle approximation of firstorder consistency based on the derivatives of temperature of neighboring particles.The numerical results calculat⁃ed by a numerical example are in good agreement with analytical solutions and results obtained from the finite ele⁃mentmethod,which proves that the proposedmethod is accurate and stable.

transient heat conduction;boundary treatment;meshless symmetric particlemethod

O242

A

2014-05-25

国家自然科学基金项目（11302077）；江西省“井冈之星”青年科学家培养计划项目（20112BCB23013）；江西省教育厅科技项目（GJJ14398）

肖毅华（1984—），男，讲师，博士，主要研究方向为无网格法及其应用。

1005-0523（2014）04-0065-06