基于Modelica的电动汽车悬架系统建模与仿真分析＊

刘炜 吴义忠 陈立平 熊会元

（1.华中科技大学；2.中山大学）

基于Modelica的电动汽车悬架系统建模与仿真分析＊

刘炜1吴义忠1陈立平1熊会元2

（1.华中科技大学；2.中山大学）

基于多领域统一建模的标准语言Modelica建立了电动汽车悬架系统模型库，并以一款电动客车的悬架系统为研究对象，对其操纵稳定性和行驶平顺性进行仿真分析，验证了悬架系统建模的准确性。采用正交试验方法对行驶平顺性进行了优化。仿真和优化结果表明，所设计悬架能够满足电动汽车的性能需求。

1 悬架系统建模

本文以一款电动客车的悬架系统为研究对象，评价和分析了悬架系统的平顺性表现。该电动客车前悬架为麦弗逊式悬架，后悬架为双连杆式悬架。

1.1 麦弗逊式前悬架模型

麦弗逊式悬架是独立前悬架，普遍应用在轻型客车和轿车上，最大的设计特点是结构简单。麦弗逊式悬架主要由车身、减振器、螺旋弹簧、转向节总成、转向横拉杆、转向器齿条、下摆臂和车轮总成组成。对悬架构件间的连接形式进行抽象简化，简化后的悬架构件连接关系如表1所示，运动副简化遵守的原则是保证悬架的自由度合理。

表1 麦弗逊式前悬架模型中的运动副

计算1/2麦弗逊悬架的自由度:

麦弗逊式悬架自由度为2，分别为车轮上、下跳动和绕主销轴线旋转，因此运动约束关系简化后的模型自由度符合要求。考虑到减振器和螺旋弹簧对悬架性能影响不大，将减振器和螺旋弹簧简化为线性阻尼和弹簧力元组件。

根据悬架的物理结构，按照层次关系建模，主要利用Modelica标准库的Mechanics子模型库[1]创建1/2麦弗逊式前悬架模型如图1所示。

本文悬架的转向系统采用齿轮齿条式转向系统，其模型如图2所示。

其他的主要部件模型有立柱减振器、A字型摆臂、轮毂和转向节模型。根据悬架的对称性，将两个1/2麦弗逊式悬架模型和转向系统模型、轮毂模型装配起来，建立麦弗逊式前悬架模型，模型参数由record模型保存，如图3所示。

1.2 双连杆式后悬架模型

双连杆式后悬架是麦弗逊式悬架系统中的一种，但与传统麦弗逊式悬架系统不同的是，双连杆式后悬架将单一A字型下摆臂改为了具有两支点的双连杆和伸向前方的纵臂。双连杆式悬架结构继承了传统麦弗逊悬架结构简单、节省空间的优点，响应快捷灵敏。双连杆后悬架左、右对称，由副车架、后横摆臂、前横摆臂、轮毂、纵向控制臂、支撑臂、减振器和弹簧组成。对悬架构件间的连接形式进行抽象简化，简化后的悬架构件连接关系如表2所示。

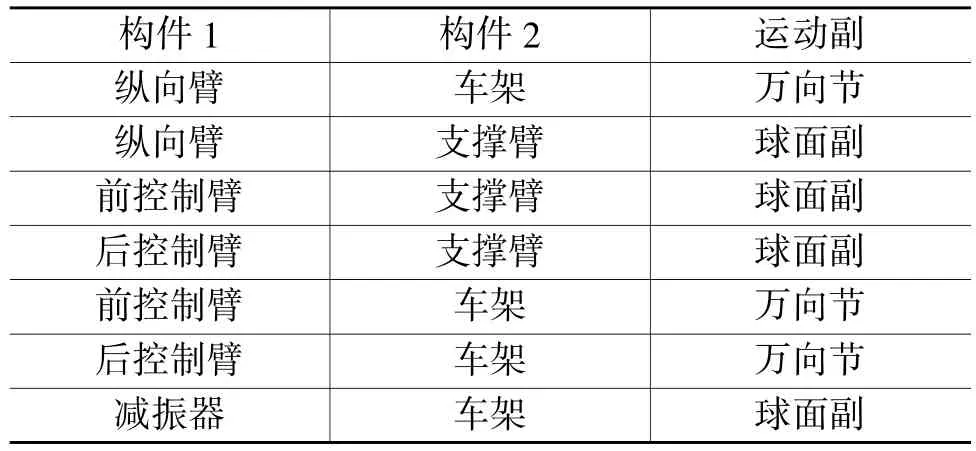
表2 双连杆式后悬架模型中的运动副

1/2 双连杆式后悬架的自由度为1，即轮毂的上、下跳动:

根据简化后的双连杆式后悬架结构和运动副，利用Modelica标准库里的组件模型，综合可视化拖放建模和文本建模方式，建立1/2双连杆式后悬架模型如图4所示。

悬架左右对称，将2个1/2悬架模型和轮毂组合起来，再加入包含模型参数的record模型，装配成完整的双连杆式后悬架模型，如图5所示。

1.3 其他部件模型

为了后续的仿真分析和试验，建立简化的轮胎模型和试验装置模型。当轮胎气压一定时，垂直方向力与变形量曲线在轮胎初始受力阶段有一段呈非线性，随着垂直力的增加，垂直力与变形量呈线性关系。虽然轮胎垂直力与变形量之间为非线性关系，但在行驶振动力学建模时，可以把轮胎简化为一个线性弹簧[2]。轮胎存在阻尼，但相对减振器阻尼而言很小，故可以忽略不记。

试验装置与车轮作用，使车轮按照给定的信号上、下跳动，模拟不平路面的行驶工况、制动点头、加速后仰、转弯侧倾等，用来测试悬架系统的各种性能。试验装置模型主要由可控移动副、平面副、旋转副等组成，如图6所示。

2 悬架性能仿真分析

2.1 左、右车轮平行跳动仿真

悬架运动学参数（如前轮定位参数和轮距等）能够决定和反映悬架操纵稳定性，本文利用左、右车轮平行跳动试验分析悬架运动学参数。车轮同向平行跳动引起的悬架运动是分析悬架运动特性的基本方法，是对车轮遇到障碍物、路面不平、汽车加减速时车身纵倾和车身侧倾等引起悬架运动的综合分析。在左、右车轮处对悬架施加合理的跳动量，计算出所需参数，进而分析和评价悬架运动学特性对汽车操纵性等性能的影响，仿真模型如图7所示。根据仿真需求，设置模型参数和初始化值。左、右车轮平行跳动仿真模型的参数主要是悬架结构的几何尺寸和硬点坐标值，这些参数从CAD软件建立的悬架三维模型中直接获得。

设定车轮跳动量为-50～50mm，仿真得到车轮定位参数随跳动量变化的曲线如图8～图12所示。

分析仿真结果可知，外倾角、主销后倾角、主销内倾角和轮距的变化满足悬架运动学设计要求，能够实现较好的悬架稳定性。而前束角在车轮上跳时呈弱负前束变化，最大变化为2.1°，超出了0～0.5°的理想范围[3]。

2.2 平顺性脉冲输入行驶仿真

影响汽车平顺性的主要部件有悬架、轮胎、座椅等，其中悬架的影响最为显著。根据GB/T4970—2009《汽车平顺性试验方法》[4]，平顺性脉冲输入行驶试验方法是让汽车以规定的车速匀速驶过三角凸块，测量各测试部位的加速度时间历程。三角凸块的尺寸和试验车速有标准规定。本文利用平顺性脉冲输入行驶试验方法来仿真分析悬架的平顺性。脉冲输入行驶试验用座椅坐垫、座椅背靠、乘员脚底地板、车厢地板处的最大加速度响应与速度v的关系来评价。最大绝对值加速度响应为:

平顺性脉冲输入行驶仿真模型主要由麦弗逊式前悬架模型、双连杆式后悬架模型、试验台模型、轮胎模型、车身模型和控制信号组成，如图13所示。平顺性脉冲输入行驶仿真模型的几何参数从CAD软件建立的悬架三维模型中直接获得；通过给CAD模型添加材料属性，利用CAD软件的分析功能获得质量、转动惯量和质心参数；悬架弹簧刚度和阻尼器阻尼系数通过计算获得。

悬架的弹簧刚度系数Ks和悬架质量固有频率fs有如下关系:

悬架的阻尼器阻尼系数Cs和阻尼比参数δ有如下关系:

根据悬架的设计需求，选定fs和δ后，就可以根据式（2）和式（3）确定Ks和Cs。轮胎刚度选取轮胎垂直特性线性阶段的刚度。

给控制器设定参数进行仿真求解，分别模拟汽车以车速10 km/h、20 km/h、30 km/h、40 km/h、50 km/h、60 km/h驶过凸块，记录车身质心处的垂向加速度时间历程。根据仿真结果，得到每个测试车速下质心处的最大绝对值加速度响应如表3所示。

表3 不同车速下的最大绝对值加速度

座椅传递给乘员的最大绝对加速度响应超过31.44m/s2时，将对人体健康造成影响[5]。当车速在10～60km/h范围内时，车身质心处的最大绝对值加速度响应先增大，然后基本保持不变，最大值为5.35m/ s2，远小于规定的上限值，因此该悬架系统能够满足汽车的平顺性要求。

2.3 整车仿真

把悬架系统模型集成到电动客车整车模型中，只需将悬架的接口与其他对应模型进行连接即可，整车模型如图14所示。在特定的循环工况下进行仿真，仿真后得到电动汽车的行驶速度曲线如图15所示，可以看出汽车实际速度与设定的要求速度非常接近，跟随性很好，说明悬架系统模型配合电池、电机、驾驶员、控制器、制动、轮胎、传动系统和自动变速器等其他电动汽车部件模型，能够很好地完成整车性能仿真分析，悬架系统模型达到了预期目标。

3 平顺性的正交试验优化

通过正交试验设计，分析所关注因素对悬架平顺性表现的影响程度，并找出在所有试验参数组合中使悬架平顺性表现最好的一组参数组合。平顺性的正交试验优化基于平顺性脉冲输入行驶仿真，选择悬架系统中对整车平顺性影响最大的参数[6]，即前、后悬架的弹簧刚度和阻尼器阻尼作为影响因素，以车身质心处最大垂向绝对值加速度响应为优化对象，优化目标为其最小化。选用L9_3_4正交表进行试验，即3个水平、4个因素、9次试验。4个影响因素分别是:F1为前悬架弹簧刚度，F2为前减振器阻尼，F3为后悬架弹簧刚度，F4为后减振器阻尼；3个水平分别是:L1为原值的0.9倍，L2为原值，L3为原值的1.1倍。根据正交表的组合，进行9次仿真，选定车速为60 km/h，仿真参数组合和结果如表4所示。

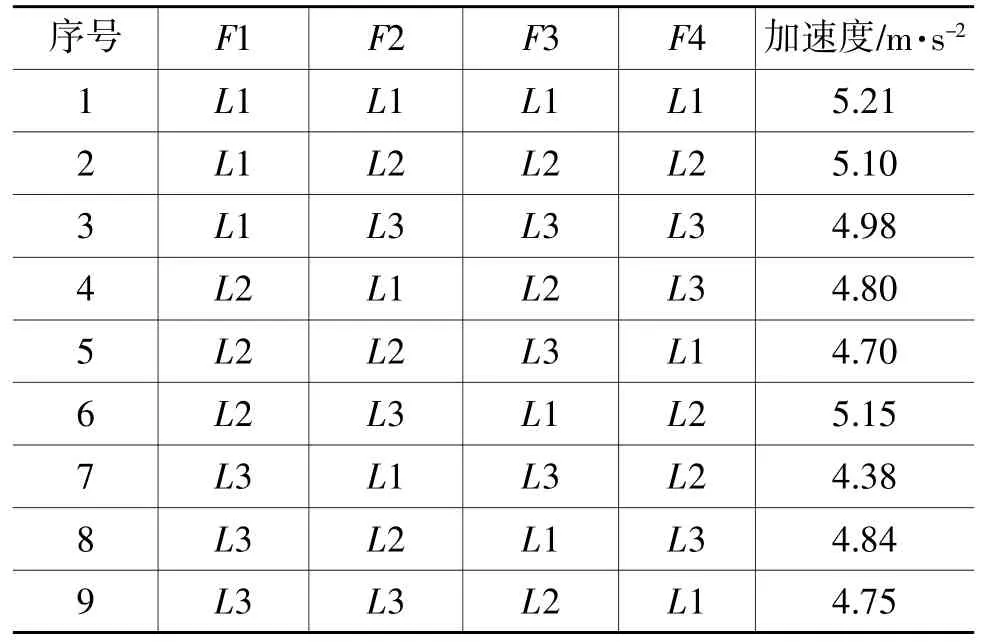
表4 随机输入平顺性仿真正交试验设计

根据试验结果计算各因素每次试验指标的平均值和极差如表5所示。均值为各因素某一水平所对应的每次试验指标之和的平均值，极差为每个因素所对应均值的最大值与最小值之差。

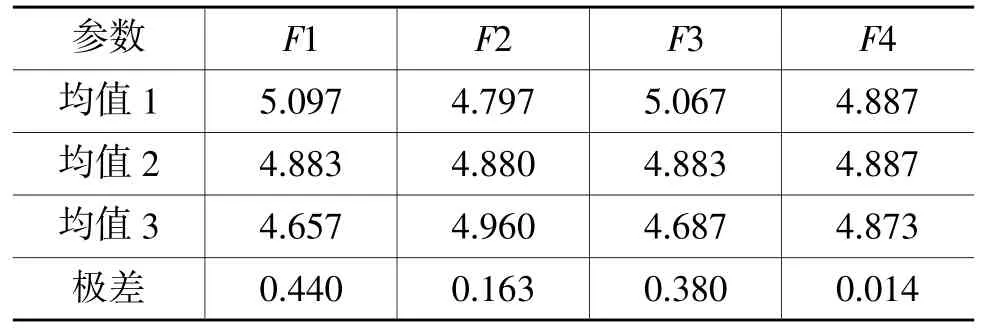
表5 最大垂向加速度的平均值和极差

通过对各因素各次试验中最大垂向加速度的平均值和极差分析，得到最优参数组合和各因素对最大绝对垂向加速度的影响程度:最优组合为F1（L3）F2（L1）F3（L3）F4（L3），此时最大垂向加速度为4.38 m/s2，小于原设计值对应的5.07m/s2；各因素对试验目标的影响程度为F1＞F3＞F2＞F4。

4 结束语

建立了基于Modelica语言的悬架系统模型库，以某款电动客车为研究对象，通过左、右车轮平行跳动仿真，进行了前悬架车轮定位参数的匹配设计和操纵稳定性分析，通过平顺性脉冲输入行驶仿真，评价和分析了悬架系统的平顺性表现，并利用正交试验设计方法对其进行了优化。

通过仿真分析，验证了基于Modelica语言的悬架系统模型的正确性。后续工作中，将把悬架模型与电机、电池、控制器、制动、传动系统等电动汽车的其他组件模型装配起来，进行电动汽车整车仿真分析。本文研究表明，基于Modelica的多领域统一建模仿真为电动汽车的参数快速匹配设计、性能分析和优化提供了一种高效的方法。

1闫雪.纯电动汽车的操纵稳定性和平顺性研究:[学位论文].南昌:南昌大学，2012.

2郑湘南.电动汽车平顺性及结构性能参数影响的分析.北京:北京交通大学，2006.

3麻友良，严运兵.电动汽车概论.北京:机械工业出版社，2012.

4赵建军，丁建完，周凡利.Modelica语言及其多领域统一建模与仿真机理.系统仿真学报，2006，18（z2）:570～573

5 Fritzson P.Principles of object-oriented modeling and simulation with Modelica 2.1.New York:IEEE Press，2003.

6李斌，陈立平，黄正东，等.基于MWorks的机械系统仿真实验研究.科技创新导报，2012（28）:6～7.

7 Otter M，Elmqvist H，Mattsson S E.The new modelica multibody library//Proceedings of the 3rd International Modelica Conference.Linköping，The Modelica Association and Linköping University，2003

8丁能根，余贵珍.汽车动力学及其控制.哈尔滨:哈尔滨工程大学出版社，2009.

9杨树凯.独立悬架性能评价指标与评价方法及其在双横臂与多连杆式悬架上的仿真实现:[学位论文].长春:吉林大学，2005.

10国家发展和改革委员会.GB/T 4970—2009汽车平顺性试验方法.北京:中国标准出版社，2009.

（责任编辑帘青）

修改稿收到日期为2014年3月1日。

Modeling and Simulation Analysis of Electric Vehicle Suspension Based on M odelica

Liu Wei1,Wu Yizhong1,Chen Liping1,Xiong Huiyuan2
（1.Huazhong University of Science and Technology;2.Sun Yat-sen University）

In this paper,the model library of electric vehicle suspension system has been established based on multi-domain unified modeling language-Modelica.We take suspension of an electric bus as research object to make simulation and analysis of the handling stability and riding com fort,which prove accuracy of the established model.An optimization based on orthogonal experimentmethod is carried out for riding com fort.The simulation and optimization results show that the designed suspension canmeet the requirements of electric vehicle.

M ulti-domain unified modeling,Suspension,M odelica,Electric vehicle

多领域统一建模悬架系统Modelica电动汽车

U463.33

A

1000-3703（2014）09-0043-05

东莞市重大科技专项（编号:2011215155）。