稀疏过程下双Cox混合再保险风险模型的破产概率

蒋兰青

（闽江师范高等专科学校，福建福州350108）

稀疏过程下双Cox混合再保险风险模型的破产概率

蒋兰青

（闽江师范高等专科学校，福建福州350108）

研究了一类带投资和干扰的双险种再保险模型，考虑保单到达过程和理赔过程均为Cox过程，且后者是前者的一个p-稀疏过程，针对该改进模型，得到破产概率满足的上界及推广的Lundberg不等式。

稀疏过程；Cox过程；再保险；破产概率

0 引言

我们知道，经典风险模型［1］及很多推广模型中均假设保费到达过程与理赔到达过程是独立的，但事实上，保单卖出越多其发生的理赔次数也会相应地增多，因此保单的到达和理赔的发生应该是相关的。据此有些文献讨论了二者的另一种相依关系，即将理赔过程视为保单到达过程的一个稀疏过程。文献［2］研究了在此相依关系之上，保单与理赔到达过程均为复合Poisson过程的风险模型，得到了有关破产概率的诸多结论。然而保单到达数与理赔次数的强度是随机改变的，用强度不变的齐次Poisson过程来描述必然存在很大的局限性，若用Cox风险模型研究更符合实际经营的需要，其结果也更有现实意义。文献［3］研究了保费的到达和理赔的发生都服从Cox过程的双险种风险模型，得到了破产概率满足推广的Lundberg不等式，并且得到了累积强度均为常数时ψ(0)的明确表达式。

本文在文献［2-3］的基础上，将稀疏过程及Cox过程引入再保险模型中，建立了带投资和干扰的风险模型，考虑保单到达过程和理赔过程均为Cox过程，且后者是前者的一个p-稀疏过程，针对该改进模型，得到破产概率满足的上界及推广的Lundberg不等式。

1 预备知识与模型建立

定义1［4］随机过程以概率1满足：

（i）Λ(0)=0；（ii）∀t＜∞，Λ(t)＜∞；（iii）其实现是t的单调不减的连续函数，则称Λ是一个（扩散）随机测度。

不妨假设下面讨论所遇到的随机测度都是扩散的，且当t→+∞时，Λ(t)→+∞，P-a.s.。

定义2［4］Poisson过程{˜(t)，t≥0}称为标准Poisson过程，若其强度

定义3［3］假设{Λ(t)，t≥0}是随机测度，{(t)，t≥0}是标准Poisson过程，且Λ(t)与(t)是相互独立的，则点过程N(t)=(t)◦Λ(t)=(Λ(t))称为Cox过程（或者称为重随机Poisson过程），其中Λ(t)又称为累积强度过程。若假设显然以概率1有λ(t)≥0，{λ(t)，t≥0}称为强度过程。

引理1［3］如果Λ(t)是随机测度，且假设E[Λ(t)]＜+∞，FΛ∞=σ(Λ(s)，s≤∞)，则N(t)是相应的Cox过程，当且仅当满足下列条件：

（i）N(t)对FΛ∞有条件独立增量；

（ii）N(t)-N(s)对FΛ∞服从均值为Λ(t)-Λ(s)的条件Poisson分布，即对任意的0≤s＜t和非负整数k，有概率表达式：

定义4假定事件E的发生形成强度为Λ(t)的Cox过程{M(t)， t≥0}，如果每一发生的事件只以概率p被记录到（0＜p＜1），记录到的事件发生的次数{N(t)， t≥0}被称为{M(t)， t≥0}的一个随机稀疏，此时{N(t)， t≥0}是强度为pΛ(t)的Cox过程。

本文同样考虑成数与超额赔款混合再保险［5-6］，且假定原保险公司先选择了一个自留比例为a的成数再保险，按此比例支付保费并提取佣金；在成数再保险的基础上又安排了一个自留额为M的超额赔款再保险。于是，当索赔为Y时，原保险公司在索赔发生时的自留额为h(Y)=min{aY，M}，超额再保险支付Y-h(Y)=max{0，aY-M}。假设成数再保险的保费按原始条款计算，而超额赔款再保险保费计算根据期望值原理，且安全附加系数为α＞0。再者考虑将一部分初始资金用于固定投资，这样，原保险公司在t时刻的盈余过程和盈利过程分别为

化简得

其中，

①u≥0为保险公司的初始资金，u˜表示根据初始资金而设定用于投资的资金，h是单位时间的投资收益；

②{Xi，i≥1}，{Yj，j≥1}是取值于[0，+∞)上非负独立同分布的随机变量序列，分别表示保险公司在第i次的保费收入及第j次的理赔额，设其分布函数分别为F(x)，G(y)，均值分别为μ1， μ2，且对x≤0有F(x)=0，对y≤0有G(y)=0；

③{N(t)，t≥0}是强度为{Λ(t)，t≥0}的Cox过程，表示保单的到达过程；

④{Np(t)，t≥0}是过程{N(t)，t≥0}的p-稀疏过程，即{Np(t)，t≥0}是强度为{pΛ(t)，t≥0}的Cox过程，表示理赔的到达过程。这里假定每个保单持有者理赔与否为相互独立，持保人以相同概率理赔，p的含义为：由过去的经验知，发生事故时，会以概率p引起理赔，且0＜p＜1，否则此险种无经济价值；

引理2对于盈余过程，存在关于FΛ∞可测的函数ga，M(r，t)，使得证明由（2）式及引理1知：

其中，

于是有

其中MX(r),Mh(Y)(r)分别是X，h(Y)的矩母函数。令

则引理2得证。

引理3设是鞅。

证明假设t＞s，由引理1、引理2得

2 最终破产概率与推广的Lundberg不等式

定理1对于任意的实数r，最终破产概率满足不等式

证明对任意取定的t0＜+∞，T∧t0为有界停时，因此由Doob-有界停时定理［7］知：

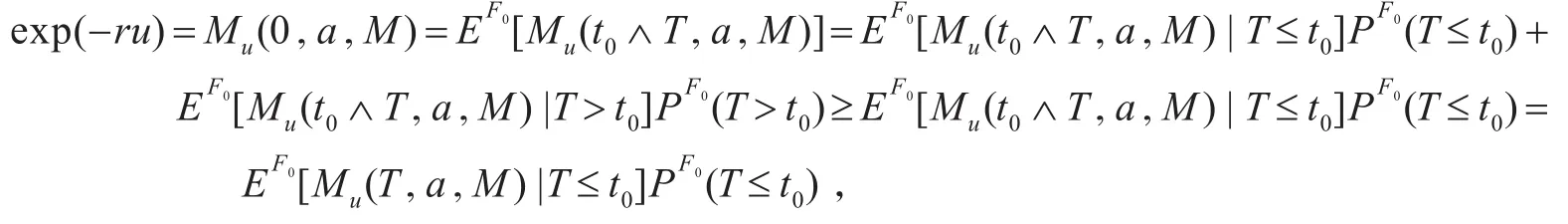
当T＜∞时，u+S(T)≤0，于是有

两边同时取期望得

定义5令称R为模型（1）的Lundberg指数。

定理2对任意的0＜ε＜R，有

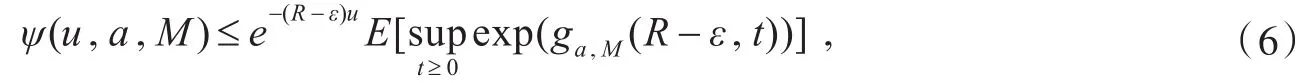
证明由（5）式知，其中r≤R，又由定义5知从而对每一个满足0＜ε＜R的ε，有0＜R-ε＜R，将（5）式中的r换成R-ε，（5）式仍然成立，即有ψ(u，a，M)≤e-(R-ε)u

（References）

［1］ØKSENDAL B.Stochastic differential equations［M］.New York：Springer-Verlag，2000.

［2］赵金娥，王贵红，龙瑶，等.索赔为稀疏过程的双复合Poisson风险模型［J］.经济数学，2010，27（4）：86-92.

［3］曾霭林，林祥，张汉君.双险种的Cox风险模型［J］.数学理论与应用，2003，23（1）：107-112.

［4］GRANDELL J.Aspects of risk theory［M］.New York：Springer-Verlag，1991.

［5］孙映霞，刘庆平.带干扰的常利率超额再保险Poisson风险模型的最优自留额［J］.数学理论与应用，2009，29（4）：20-24.

［6］程兰芳.确定最优比例再保险决策模型研究［J］.管理科学，2003，16（3）：43-45.

［7］成世学.破产论研究综述［J］.数学进展，2002，31（5）：403-422.

（责任编辑：强士端）

Ruin Probability of Double Cox Mixed Reinsurance Risk Model Under Thinning Process

JIANG Lanqing
（Minjiang Teachers College，Fuzhou 350108，Fujian，China）

Researches a class of double reinsurance model with investment and interference，consid⁃ering the arrival of guarantee slip and satisfaction of a claim are both the Cox process，and the latter is a p-thinning process of the former.Towards the improved model，obtains the upper bound of ruin probability satisfaction and the lundberg inequality.

thinning process；Cox process；reinsurance；ruin probability

O211.6

A

1673-0143（2014）04-0016-04

2014-03-29

蒋兰青（1986—），女，助教，硕士，研究方向：应用概率统计。