确定性极化W态的纠缠提纯

王硕，王萍，赵志胜，王兴华

（1．中南大学信息科学与工程学院，湖南 长沙 410083；2．怀德第一中学，吉林 公主岭，136100）

确定性极化W态的纠缠提纯

王硕1，王萍1，赵志胜1，王兴华2

（1．中南大学信息科学与工程学院，湖南 长沙 410083；2．怀德第一中学，吉林 公主岭，136100）

本文针对W纠缠态提出了一种确定性纠缠提纯方案.本文通过线性光学技术作为基础例如PBS、HWP等，同时利用交叉卡尔非线性技术检测量子数，并借助组合多种自由度，克服了普通方案共有单一极化自由度的缺陷，实现了W态的提纯，又在理论上计算出成功率为百分之百，具有高效可行性.

W态；纠缠；极化提纯；自由度

量子纠缠态是量子信息处理中的一大重要资源，并广泛应用于量子通信的各个领域，然而量子在传输过程中由于量子系统受到环境噪声的影响，最大纠缠态将会减弱，无法高效传输信息.为此早在1996年，Bennett等人[1]提出了一个最早的纠缠纯化协议(Entanglement Purification Protocol,即EPP)来对Werner态进行提纯[2],协议中主要采用量子受控非门(CNOT)与双向幺正操作来实现提纯.然而这只是一种理论上的提纯方案，因为在当时的科技水平下，量子控制非门无法完美的实现，甚至直到现在也无法做到.随后,Deutsh等人[3]利用两个附加的特定酉性操作进一步完善了之前的纠缠纯化协议.在2000年，史保森等人[4]提出了一种基于纠缠交换的提纯方法，该方法主要通过将两个纠缠对中的粒子进行纠缠交换，来实现提纯.2002年,Simmon等人[5]提出一种新的EPP协议，该协议采用了一种目前可用的参量下转换(PDC)源,而不是一个理想的纠缠源.该协议利用了量子的空间纠缠特性来实现对极化纠缠的提纯，这似乎也是第一个使用空间模来对极化态进行提纯的协议.2003年,潘教授带领的团队[6]在实验中证明了Simmon所提出协议的可行性.2008年，邓富国等人提出了一种基于PDC源的高效EPP协议[7].然而,交叉卡尔非线性结构太细微的性质,增加了困难实施这EPP协议的难度.2008年,肖立等人[8]提出了一种基于频率纠缠的EPP方案.2010年，D.Salart,O.Landry,N. Sangouard等人[9]提出了一种基于线性光学组件的双空间模式间共享的单光子纠缠提纯方案，2011年，Denis Gont，Peter van Loock等人[10]创新的利用原子与光子腔链的方式，实现了对W态的提纯.

本文中我们提出了一种针对W态的高效可行的确定性纠缠提纯方案，该方案以PBS、HWP等线性光学技术为框架，并辅以交叉卡尔非线性技术实现量子数检测，同时借助空间自由度等多种自由度的组合，克服了单一极化自由度的缺陷，实现了W态的高效提纯，并且理论上成功率为百分之百.

1 W态基本状态与传输分析

三粒子极化纠缠W态可以表述如下：

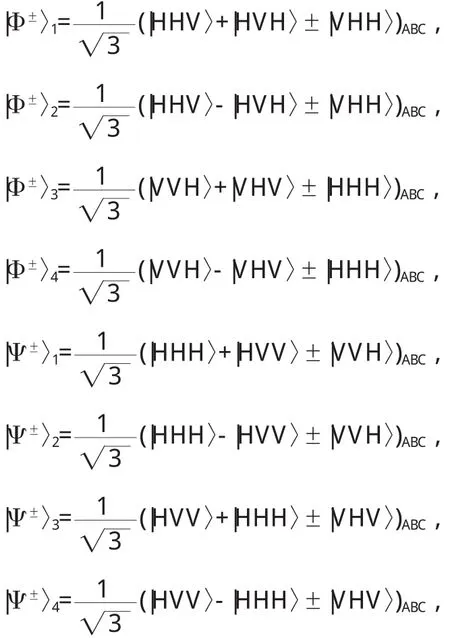
其中H，V分别代表水平与垂直极化，ABC则代表通信中的三方Alice，Bob，Charlie.而|Φ±〉1就是人们在各种量子技术中所需要的的最大纠缠态.

为提纯出最大纠缠态，引入空间自由度，则同时包含空间与极化自由度的量子纠缠系统初始态可表示为，

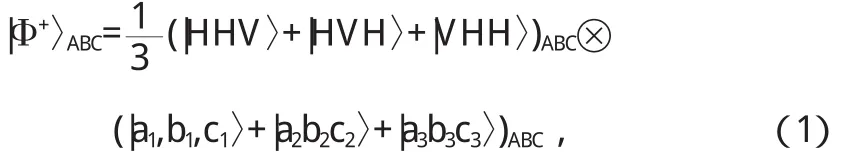
其中a,b,c分别表示三粒子系统的空间模.则有极化自由度上纠缠系统为，

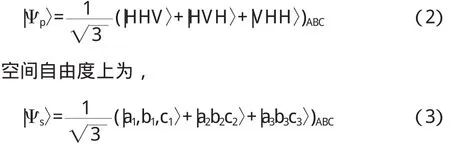
实际传输中，由于与环境的相互作用，极化态会受到一些影响，出现相反转与位翻转错误，因此传输后的状态将会一种混合的杂乱的状况.然而对于空间自由度来讲，不存在位翻转错误，而相反转错误也可以通过严格控制信道长度来消除.用测量基在极化态上对传输态进行测量后得到结果可以表述如下，

其中系数Fi表示各种量子态所占比率.此时包含两种自由的系统密度矩阵为其|.则量子系统成为八种态的概率混合，比如处于的概率为F0，处于的概率为F4.

2 W态提纯方案设计

该方案利用PBS和HWP两种线性光学组件，通过各种反射等作用将不同的输入引入不同的出口，实现了不同情况的区别对待.同时对出口处流出的粒子进行进一步处理，得到所需要的最大纠缠态.方案基本结构图如下，

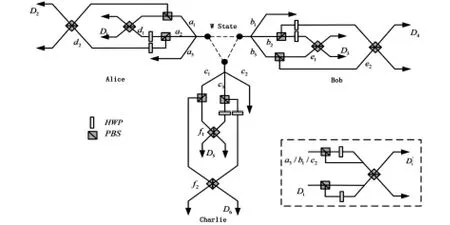
图1 确定性极化W态纠缠提纯方案示意图

方案分Alice，Bob，Charlie三端设计了相似的提纯结构，主要区别在于每一端针对单独处理的量子空间模.每一空间模对应的粒子都至少要经历两个PBS的处理，个别还需经由一个HWP处理.下面就以态|HHH〉⊗|ψs〉的提纯为例来描述一下具体的提纯流程.

当处于空间模{a2，b3，c1}的光子通过PBS与HWP之后上述状态变为

而处于空间模{a1&d1,b2&e1,f1&c3}的光子通过PBS之后，结果为

最后，由空间模{D1&a3,b1&D3,c2&D5}处得到的结果经过上图中（b）部分处理，结果如下，

由上式可见由输出端口D1’&D3’&D5’处得到的结果即为最大纠缠态，这说明方案针对|HHH>态是可行的，类似的针对其它的七种状态，经验证该方案也是可行的，只不过不同状态提纯出口不同.

根据该方案，对于混合态中的各种状态都可以有效提纯，使得Alice，Bob，Charlie三方均能获得最大极化W纠缠态.理论上，该方案提纯成功率为百分之百.

然而，这个方案却有着一个很大的问题，即在当今技术条件下，对于出口处得到的粒子，很难通过复杂的单光子检测技术实现重选(Postselection)，最终达到检测量子数的目的.针对这一问题，本文采用交叉卡尔非线性方法来构造量子非破坏检测门（Quantum nondemolition,简称QND）（图2）[11]，并以此替代出口处的PBS，从而改善这种情况.

如果相干态|ϑ〉与单光子|ψ〉=|α〉+β|1〉通过交叉卡尔非线性结构发生相互之间的作用，则单光子系统会变成以下状态：

Uck|ψ〉|ϑ〉=(α|0〉+β|1〉)|ϑ〉=α|0〉|ϑ〉+β|1〉|ϑeiθ〉（9）

其中0，1为福克态，分别表示没有光子和一个光子，而θ=χt，t表示作用时间.很明显粒子数的检测就直接转移到了相干态的相移上.

图2 交叉卡尔非线性技术构造的QND示意图

假设Alice拥有处于空间模a1a2的态|Φ〉2与相干态|α〉作用结果如下，

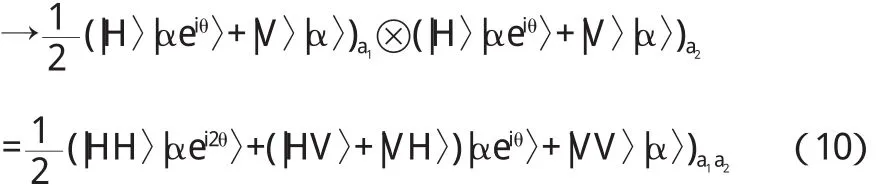
上式可见|HH>与|VV>态分别有2θ的相移和0相移，而其他两态|HV>与|VH>都有着θ的相移.通过零差检测，Alice可以保留有着2θ和0相移的|HH>与|VV>态，同时舍弃|HV>与|VH>态.根据图2.3结构，Alice可以从D1获得|HH>态，而从D2处获得|VV>态.同理，Bob和Charlie均可从对应出口处获得|HH>与|VV>态.假设初态是|HHH〉⊗×ψs〉，则可从空间模{D1&a3，b1&D3,c2&D5}处获得结果态，再经图3中(b)部分的HWP与PBS结构加以处理，通信三方则可在{D1’，D3’，D5’}处获得如上式(9)所示的最大纠缠态.对于初态处于其他状态的情况，该方案同样可以有效地实现提纯.

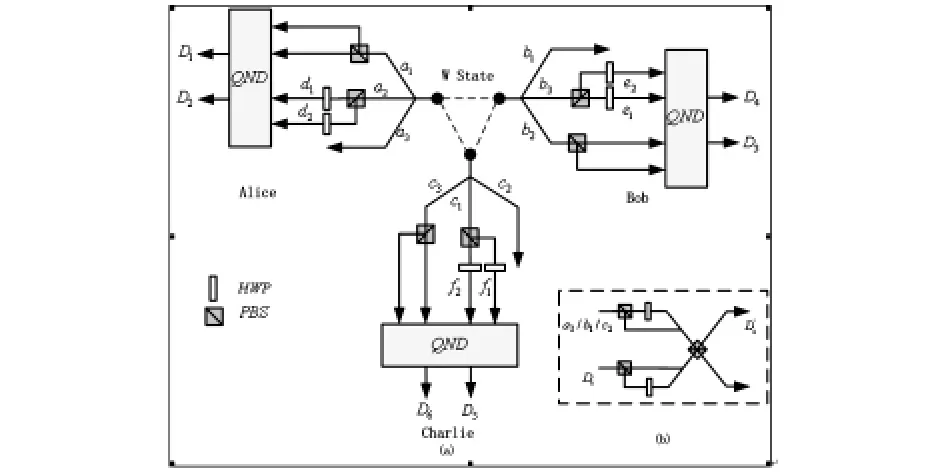
图3 使用QND结构代替尾端PBS之后的提纯方案示意图

3 结论

方案以PBS+HWP等线性光学技术为基本框架，采用交叉卡尔非线性技术加以辅助，同时利用多种自由度对信道噪声抗干扰性能的不同，有效地弥补了单一极化自由度易受噪声干扰的不足，实现了有效的提纯.最终成功实现GHZ态以及Cluster态的确定性极化纠缠提纯，根据理论分析能高效的完成两种纠缠态的提纯，并且理论成功率均为100%.

〔1〕Bennett C.H,Brassard G,Popescu S,Schumacher B,Smolin J.A,and Wootters W.K,Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels[J],Phys.Rev.Lett.1996,76(5),722～725.

〔2〕Werner R.F,Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden variable model[J],Phys.Rev.A,1989,40(8),4277～4281.

〔3〕Deutsch D,Ekert A,Jozsa R,Macchiavello C,Popescu S,and Sanpera A,Quantum Privacy Amplification and theSecurity ofQuantum Cryptography overNoisy Channels[J],Phys.Rev.Lett.1996,77(13),2818–2821.

〔4〕Shi Bao-Sen,Jiang Yun-Kun,and Guo Guang-Can,Optimal entanglement purification via entanglement swapping[J],Phys.Rev.A,2000,62(5),054301.

〔5〕Simon C and Pan J.W,Polarization Entanglement Purification using Spatial Entanglement[J],Phys.Rev.Lett.2002,89(25),257901.

〔6〕Pan J.W,S.Gasparonl,R.Ursin,G.Weihs,and A.zellinger,Experimental entanglement purification of arbitrary unknown states[J],Nature 2003,423,417～422.

〔7〕Sheng Y.B,Deng F.G,and Zhou H.Y,Efficient polarization-entanglement purification based on parametric down-conversion sources with cross-Kerr nonlinearity[J],Phys.Rev.A,2008,77(4),042308.

〔8〕Xiao L,Wang C,Zhang W,Huang Y.D,Peng J.D,and Long G. L,Efficient strategy for sharing entanglement via noisy channels with doubly entangled photon pairs[J],Phys.Rev.A,2008,77(4),042315.

〔9〕SalartD,Landry O,Sangouard N,Purification of single-photon entanglement[J],Phys.Rev.Lett.2010,104(18),180504.

〔10〕Denis Gont,Peter van Loock,Dynamical entanglement purification using chains of atoms and optical cavities[J],Phys.Rev.A,2011,84(4),042303.

〔11〕赵春然.Cross-Kerr介质在量子信息中的应用[D].安徽：安徽大学,2011.

0141

A

1673-260X（2014）07-0019-03